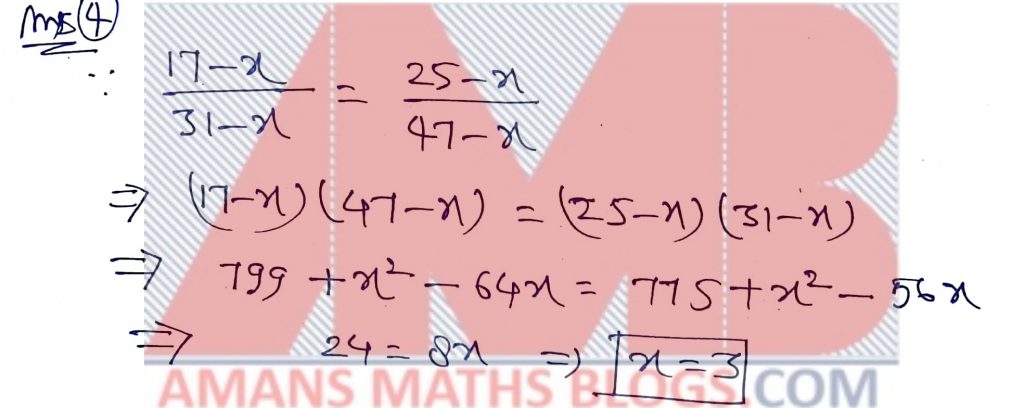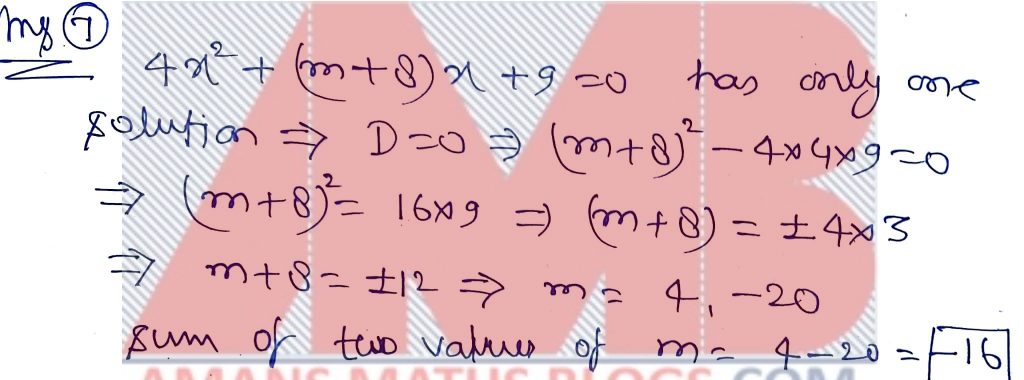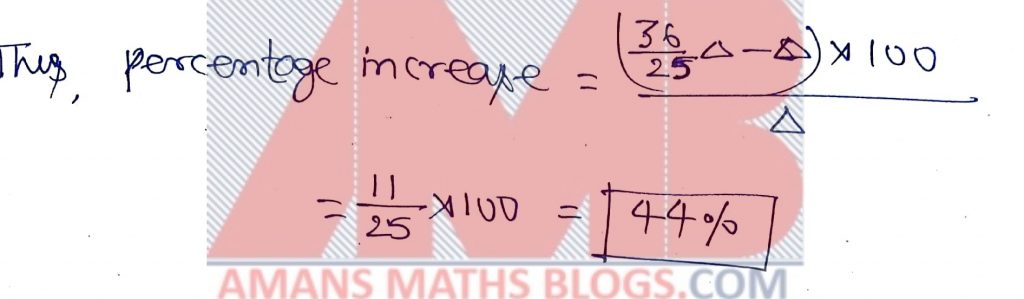NMTC 2018 Question Papers with Solutions Junior Level
NMTC is an acronym for National Mathematics Talent Contest. NMTC is conducted by AMTI (Association of Mathematics Teachers of India) to identify the talent of the students in Mathematics. In this post, NMTC 2018 Question Papers with Solutions Junior Level is published.



Click Here NMTC 2019 Notification
Part A: Instruction:
Only One of the choices A, B, C, D is correct. For each correct response, you get 1 mark. For each incorrect response, you lose 1/2 mark. NMTC 2018 Question Papers with Solutions Junior Level
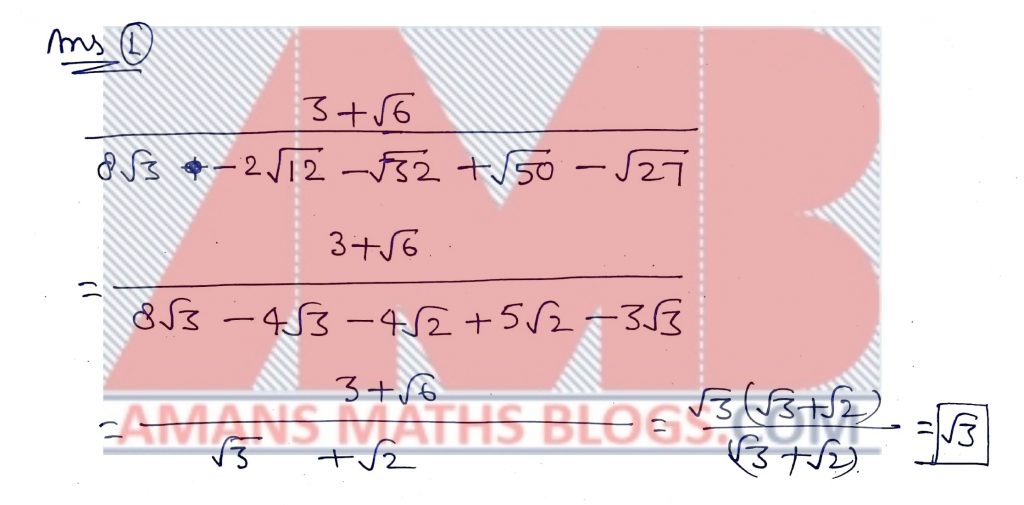
NMTC 2018 Paper For Junior Level Ques No 1:
The value of
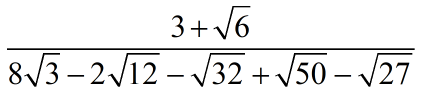
is
Options:
A.
B.
C.
D.
Solution:
NMTC 2018 Paper For Junior Level Ques No 2:
A train moving with a constant speed crosses a stationary pole in 4 seconds and a platform 75 m long in 9 seconds. The length of the train is (in meter)
Options:
A. 56
B. 58
C. 60
D. 62
Solution:
NMTC 2018 Paper For Junior Level Ques No 3:
One of the factors of 9x2 – 4z2 – 24xy + 16y2 + 20y – 15x + 10 is
Options:
A. 3x – 4y – 2z
B. 3x + 4y – 2z
C. 3x + 4y +2z
D. 3x – 4y + 2z
Solution: BONUS
The given question is wrong: 9x2 – 4z2 – 24xy + 16y2 + 20y – 15x + 10
The correct question is 9x2 – 4z2 – 24xy + 16y2 + 20y – 15x + 10z.
Thus,
9x2 – 4z2 – 24xy + 16y2 + 20y – 15x + 10z
= (9x2 – 24xy + 16y2) – 4z2 + 20y – 15x + 10z
= (3x – 4y)2 – (2z)2 + 5(4y – 3x + 2z)
= (3x – 4y + 2z)(3x – 4y – 2z) – 5(3x – 4y – 2z)
= (3x – 4y – 2z)(3x – 4y + 2z – 5)
Therefore, one of the factors of 9x2 – 4z2 – 24xy + 16y2 + 20y – 15x + 10 is (3x – 4y – 2z).
NMTC 2018 Paper For Junior Level Ques No 4:
The natural number which is subtracted from each of the four numbers 17, 31, 25, 47 to give four numbers in proportion is
Options:
A. 1
B. 2
C. 3
D. 4
Solution:
NMTC 2018 Paper For Junior Level Ques No 5:
The solution to the equation 5(3x) + 3(5x) = 510 is
Options:
A. 2
B. 4
C. 5
D. No Solution
Solution: BONUS
NMTC 2018 Paper For Junior Level Ques No 6:
If (x + 1)2 = x, the value of 11x3 + 8x2 + 8x – 2 is
Options:
A. 1
B. 3
C. 3
D. 4
Solution:
NMTC 2018 Paper For Junior Level Ques No 7:
There are two values of m for which the equation 4x2 + mx + 8x + 9 = 0 has only one solution for x. The sum of these two values of m is
Options:
A. 1
B. 3
C. 3
D. 4
Solution:
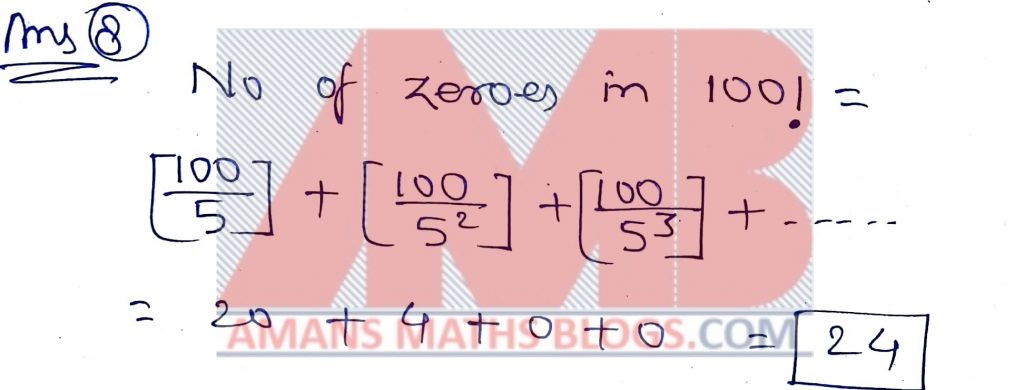
NMTC 2018 Paper For Junior Level Ques No 8:
The number of zeros in the product of the first 100 natural numbers is
Options:
A. 12
B. 15
C. 18
D. 24
Solution:
NMTC 2018 Paper For Junior Level Ques No 9:
The length of each side of a triangle is increased by 20% then the percentage increase of area is
Options:
A. 60%
B. 120%
C. 80%
D. 44%
Solution:
NMTC 2018 Paper For Junior Level Ques No 10:
The number of pairs of relatively prime positive integers (a, b) such that a/b + 15b/4a is an integer is
Options:
A. 1
B. 3
C. 3
D. 4
Solution:
NMTC 2018 Paper For Junior Level Ques No 11:
The four digit number 8ab9 is a perfect square. The value of a2 + b2 is
Options:
A. 52
B. 62
C. 54
D. 68
Solution:
NMTC 2018 Paper For Junior Level Ques No 12:
a, b are positive real numbers such that 1/a + 9/b = 1. The smallest value of a + b is
Options:
A. 15
B. 16
C. 17
D. 18
Solution:
NMTC 2018 Paper For Junior Level Ques No 13:
a, b are real numbers. The least value of a2 + ab + b2 – a – 2b is
Options:
A. 1
B. 0
C. -1
D. 2
Solution:
Let y = f(a, b) = a2 + ab + b2 – a – 2b … (1)
Differentiate y with respect to a and b separately.
On differentiating (1) w.r.t. a, we get dy/da = 2a + b – 1. For least, dy/da = 0.
Thus, 2a + b – 1 = 0 … (2)
On differentiating (1) w.r.t. b, we get dy/db = a + 2b – 2. For least, dy/db = 0.
Thus, a + 2b – 2 = 0 … (3)
On solving equations (2) and (3), we get a = 0 and b = 1.
Put a = 0 and b = 1 in equation (1). we get least value of given expression as
Minimum value of y = (0)2 + (0)(1) + (1)2 – (0) – 2(1) = 1 – 2 = -1
NMTC 2018 Paper For Junior Level Ques No 14:
I is the incenter of a triangle ABC is which A = 80 Degree. BIC =
Options:
A. 120 Degree
B. 110 Degree
C. 125 Degree
D. 130 Degree
Solution:
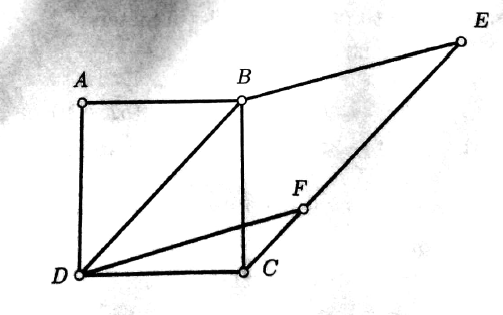
NMTC 2018 Paper For Junior Level Ques No 15:
In the adjoining figure, ABCD is a square and DFEB is a rhombus. The angle CDF = ?
Options:
A. 15 Degree
B. 18 Degree
C. 20 Degree
D. 30 Degree
Solution:
Part B: Instruction:
Write the correct answer in the space provided in the responsive sheet. For each correct response, you get 1 mark. For each incorrect response, you lose 1/4 mark.
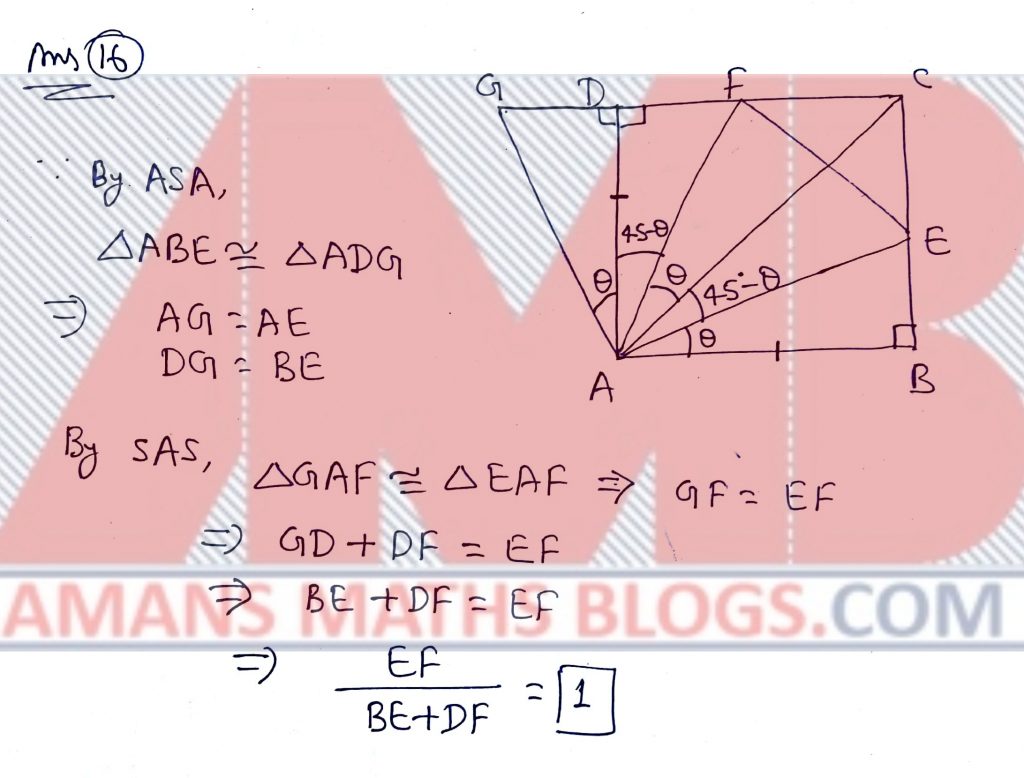
NMTC 2018 Paper For Junior Level Ques No 16:
ABCD is a square. E, F are points on BC, CD respectively and EAF = 45 Degree. The value of BF/(BE + DF) is______
Solution:
NMTC 2018 Paper For Junior Level Ques No 17:
The average of 5 consecutive natural numbers is 10. The sum of the second and fourth of these numbers is_____
Solution:
NMTC 2018 Paper For Junior Level Ques No 18:
The number of natural numbers n for which n2 + 96 is perfect square is______
Solution:
NMTC 2018 Paper For Junior Level Ques No 19:
n is an integer and

is also an integer. The sum of all such n is__
Solution:
NMTC 2018 Paper For Junior Level Ques No 20:
a/b is a fraction where a, b have no common factors other than 1. b exceeds a by 3. If the numerator is increased by 7, the fraction is increased by unity. The value of a + b_____
Solution:
NMTC 2018 Paper For Junior Level Ques No 21:
If 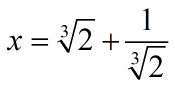 then the value of 2x3 – 6x is______
then the value of 2x3 – 6x is______
Solution:
NMTC 2018 Paper For Junior Level Ques No 22:
The angles of a heptagon are 160 Degree, 135 Degree, 185 Degree, 140 Degree, 125 Degree, x Degree, x Degree. The value of x is _____
Solution:
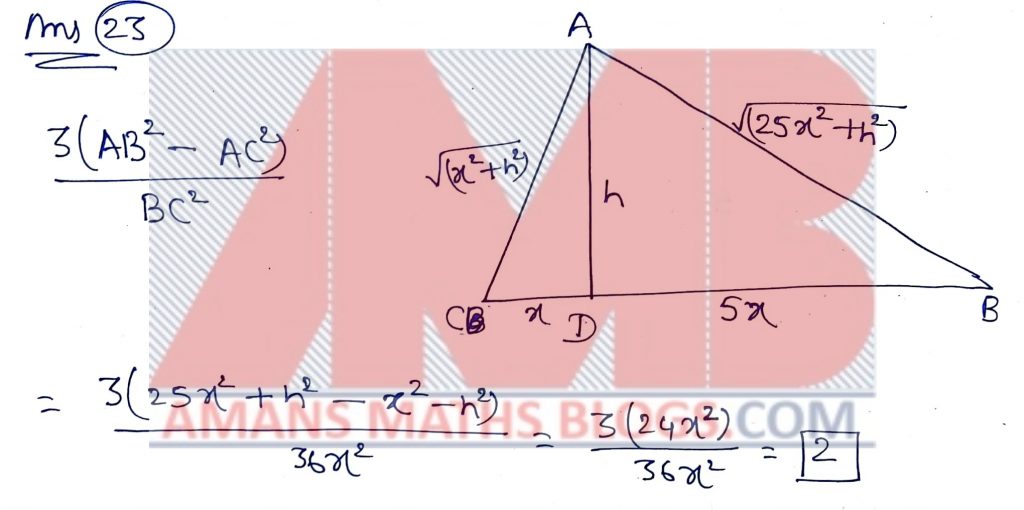
NMTC 2018 Paper For Junior Level Ques No 23:
ABC is a triangle and AD is its altitude. If BD = 5DC, then the value of

is
Solution:
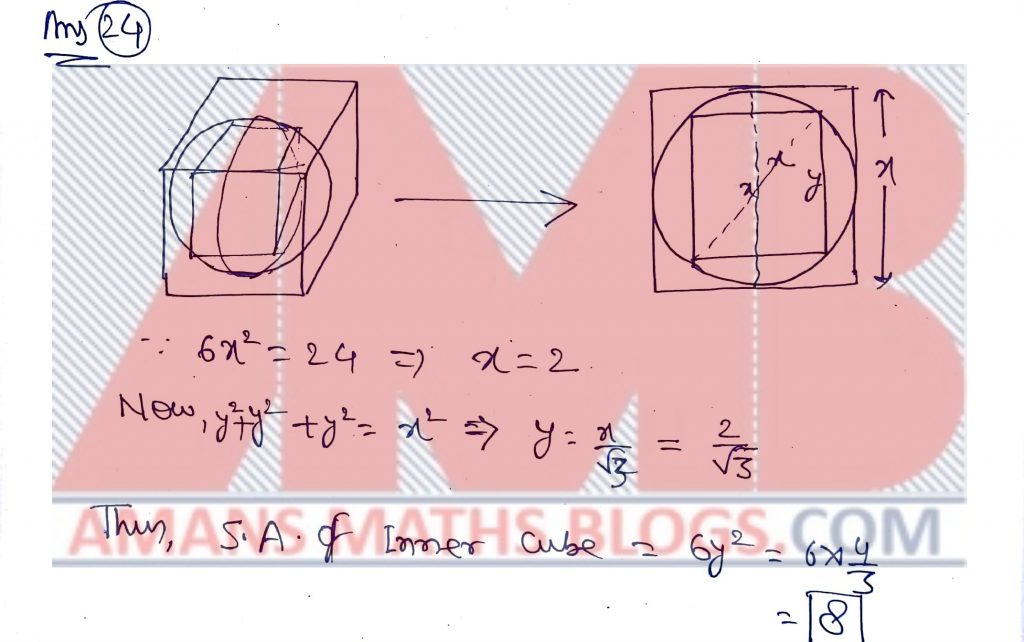
NMTC 2018 Paper For Junior Level Ques No 24:
A sphere is inscribed in a cube that has a surface area of 24 cm2. A second cube is then inscribed within the sphere. The surface area of the inner cube (in cm2) is_____
Solution:
NMTC 2018 Paper For Junior Level Ques No 25:
A positive integer n is a multiple of 7. If lies between 15 and 16, the number of possible values(s) of n is_____
Solution:
NMTC 2018 Paper For Junior Level Ques No 26:
The value of x which satisfies the equation 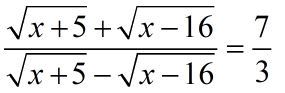 is
is
Solution:
NMTC 2018 Paper For Junior Level Ques No 27:
M man do a work in m days. If there had been N men more, the work would have been finished n days earlier, then the value of m/n – M/N is_____
Solution:
NMTC 2018 Paper For Junior Level Ques No 28:
The sum of the digits of a two number is 15. If the digit of the given number are reserved, the number is increased by the square of 3. The original number is______
Solution:
NMTC 2018 Paper For Junior Level Ques No 29:
When expanded the units place of (3127)173 is_____
Solution:
NMTC 2018 Paper For Junior Level Ques No 30:
If a : (b + c) = 1 : 3 and c : (a + b) = 5 : 7, then b : (c + a) is_______
Solution: