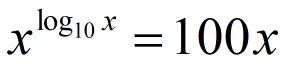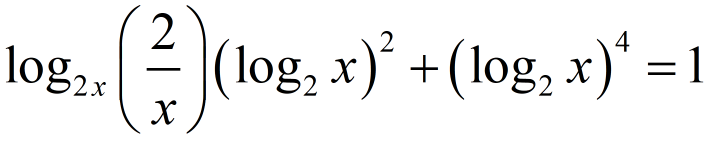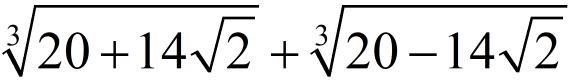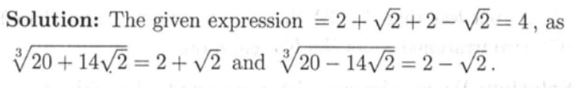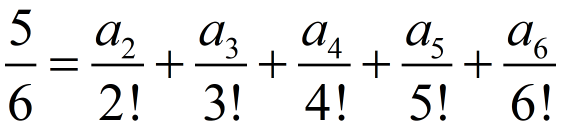NMTC 2010 Question Papers with Solutions Junior Level

NMTC is an acronym for National Mathematics Talent Contest. NMTC is conducted by AMTI (Association of Mathematics Teachers of India) to identify the talent of the students in Mathematics. In this post, NMTC 2010 Question Papers with Solutions Junior Level is published.

Part A: Instruction:

Only One of the choices A, B, C, D is correct. NMTC 2010 Question Papers with Solutions Junior Level For each correct response, you get 1 mark. For each incorrect response, you lose 1/2 mark.

NMTC 2010 Paper For Junior Level Ques No 1:

The numbers which when subtracted from the terms of the ratio a : b makes it equal to c : d is

Options:

A. (ab – cd)/(ab + cd)

B. (bc – ad)/(c + d)

C. (ab + cd)/(c + d)

D. (ab – cd)/(b – c)

Solution:

NMTC 2010 Paper For Junior Level Ques No 2

In a kilometer race, Ram beats Shyam by 25 meters or 5 seconds. The time taken by Ram to complete the race is

Options:

A. 1 minute

B. 5 minute 30 second

C. 3 minute 15 second

D. 4 minute 10 second

Solution:

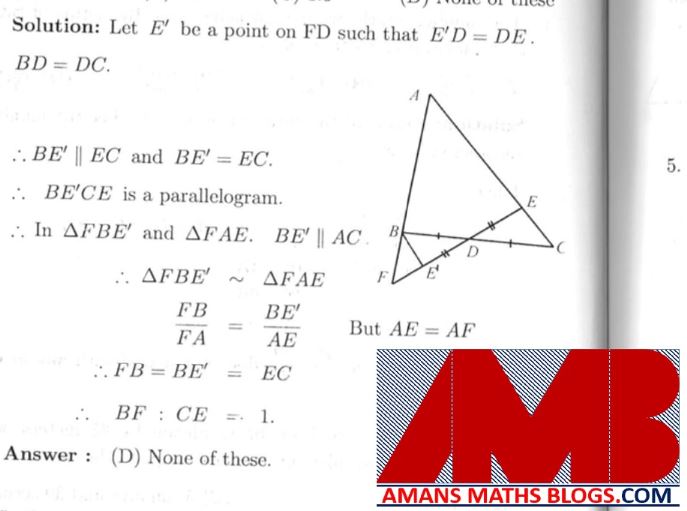
NMTC 2010 Paper For Junior Level Ques No 3

Through D, the mid-point of the side BC of a triangle ABC, a straight line is drawn to meet AC at E and AB produced at F so that AE = AF Then, the ratio of BF : CE is

Options:

A. 1 : 2

B. 2 : 1

C. 1 : 3

D. None of These

Solution:

NMTC 2010 Paper For Junior Level Ques No 4

In the bigger of two concentric circles, two chords AB and AC are drawn to touch line is drawn to touch the smaller circle at D and E, then BC is equal to

Options:

A. 3DE

B. 4DE

C. 2DE

D. (3/2)DE

Solution:

NMTC 2010 Paper For Junior Level Ques No 5

The number of solution of the equation

Options:

A. 0

B. 1

C. 2

D. 3

Solution:

NMTC 2010 Paper For Junior Level Ques No 6

The internal bisector of AE of the angle A of triangle ABC is

Options:

A. Not greater than the median through A for all triangles.

B. Not greater than the median through A for only acute angled triangles.

C. Not greater than the median through A for only obtuse angled triangles.

D. Not less than the median through A for all triangles.

Solution:

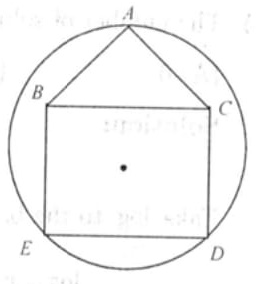
NMTC 2010 Paper For Junior Level Ques No 7

In the adjoining diagram, ABC is an equilateral triangle BCDE is a square. The side of the equilateral triangle is 2010. The radius of the circle is

Options:

A. 2010

B. 4020

C. 6030

D. 8040

Solution:

NMTC 2010 Paper For Junior Level Ques No 8

Given a and b are integers the expression (a² + a + 2011)(2b + 1) is

Options:

A. Odd for exactly 2010 values of a and b.

B. Odd for exactly 2010 values of a and b.

C. Even for exactly one value of a and two values of b.

D. Odd for exactly one value of a and one values of b.

Solution:

NMTC 2010 Paper For Junior Level Ques No 9

A real sequence of real numbers x_n is defined recursively as follows x₀, x₁, are arbitrary positive real numbers and x_n+2 = (1 + x_{n +1})/x_n, n = 0,1,2,3,…. Then the value of x₂₀₁₁ is

Options:

A. 1

B. x₀

C. x₁

D. x₂

Solution:

NMTC 2010 Paper For Junior Level Ques No 10

If xy = 6 and x²y + y²x + x + y = 63, then the value of x² + y² is

Options:

A. 81

B. 18

C. 2010

D. 78

Solution:

NMTC 2010 Paper For Junior Level Ques No 11

If p is the perpendicular drawn from the vertex of a regular tetrahedron to the opposite face and if each edge is equal to 2 units, the p is

Options:

A. $8\sqrt{3}$

B. $8\sqrt{3}$ /2

C. $8\sqrt{3}$ /3

D. $8\sqrt{3}$ /5

Solution:

NMTC 2010 Paper For Junior Level Ques No 12

The remainder when the polynomial x + x³ + x⁹ + x²⁷ + x⁸¹ + x²⁴³ is divided by x² – 1.

Options:

A. 6x

B. 2x

C. 3x

D. 1

Solution:

NMTC 2010 Paper For Junior Level Ques No 13

Consider the sequence 4, 4, 8, 2, 0, 2, 4, 6, 0, …where the nth term is the unit place of the sum of the sum of previous two terms for n ≥ 3. If Sn is the sum to n terms of this sequence, then the smallest n for which S_n > 2011 is.

Options:

A. 253

B. 502

C. 503

D. 504

Solution:

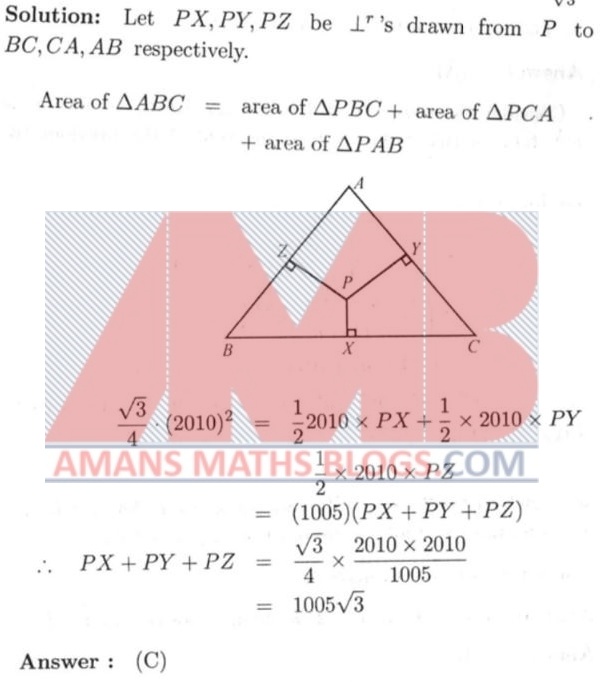
NMTC 2010 Paper For Junior Level Ques No 14

P is the point inside an equilateral triangle of side 2010 units. The sum of the lengths of the perpendiculars drawn from P to the sides is equal to

Options:

A. 2010

B. 2010 $\sqrt{3}$

C. 1005 $\sqrt{3}$

D. 2010/ $\sqrt{3}$

Solution:

NMTC 2010 Paper For Junior Level Ques No 15

The equation

has

Options:

A. A root less than 1

B. Has only root greater than 1

C. Two irrational roots

D. No real roots

Solution:

NMTC 2010 Paper For Junior Level Ques No 16

The value of

is ______.

Solution:

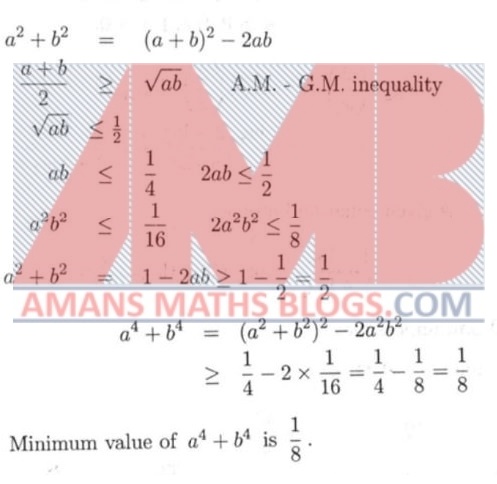
NMTC 2010 Paper For Junior Level Ques No 17

If a, b are positive and a + b = 1 then the minimum value of a⁴ + b⁴ is______.

Solution:

NMTC 2010 Paper For Junior Level Ques No 18

The whole surface area of rectangular block is 1332 cm². The length, breadth and height are in the ratio of 6:5:4. The sum of the length, breadth and height is _______ cms.

Solution:

NMTC 2010 Paper For Junior Level Ques No 19

If |x| + x + y = 10 and x + |y| – y = 12, then x + y is _____.

Solution:

NMTC 2010 Paper For Junior Level Ques No 20

Two parallel sides of a trapezoid are 3 and 9, the non-parallel sides are 4 and 6. A line parallel to the bases (parallel sides) divides the trapezoid into two trapezoids of equal perimeters. The ratio in which each of the non-parallel sides is divided is ______.

Solution:

NMTC 2010 Paper For Junior Level Ques No 21

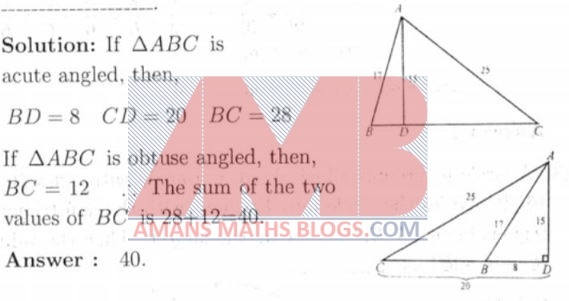
Triangle ABC has AB = 17 and AC = 25 and altitude to BC has length is 15. The sum of possible values of BC is ______.

Solution:

NMTC 2010 Paper For Junior Level Ques No 22

where 0 ≤ a_i < i, i = 1,2,3,4,5,6. Then, a₂ + a₃ + a₄ + a₅ + a₆ is ______.

Solution:

NMTC 2010 Paper For Junior Level Ques No 23

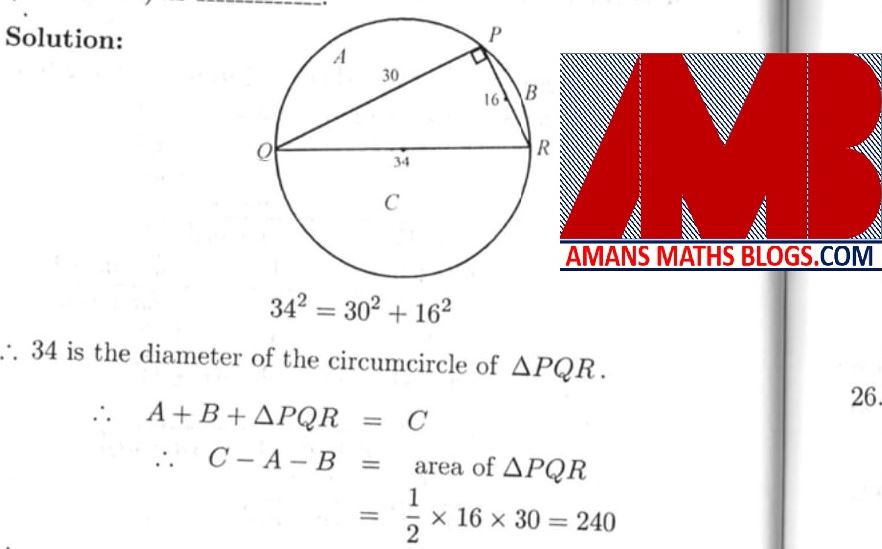
A circle is circumscribed about a triangle with sides 30, 34, 16. It divides the circle into four regions with the non-triangular regions being A, B, C. C being the largest. Then the value of (C – A – B) is ______.

Solution:

NMTC 2010 Paper For Junior Level Ques No 24

If a number n is divisible by 8 and 30, then the smallest number of divisors that n has is ______.

Solution:

NMTC 2010 Paper For Junior Level Ques No 25

Both the quadratic equation x² – 12x + K = 0 are prime numbers. The sum of all such value of K is _______.

Solution:

NMTC 2010 Paper For Junior Level Ques No 26

In a convex polygon of sides 16 sides the maximum number of angles which can all be equal to 10 degrees is _______.

Solution:

NMTC 2010 Paper For Junior Level Ques No 27

If an arc of circle 1 subtending 60 degree at the centre, has double the length as the arc subtending 75 degrees at the centre in the circle 2, then the ratio of (Area of Circle 1)/ (Area of Circle 2) is ______.

Solution: