Hi students, Welcome to AMBiPi (Amans Maths Blogs). In this article, you will get MCQ Questions for Class 10 Maths Chapter 14 Statistics with Answer Keys PDF. You can download this PDF and save it in your mobile device or laptop etc.
MCQ Questions for Class 10 Maths Chapter 14 Statistics Question No 1:
The median and mode respectively of a frequency distribution are 26 and 29, Then its mean is
Option A : 27.5
Option B : 24.5
Option C : 28.4
Option D : 25.8
Show/Hide Answer Key
Option B : 24.5
MCQ Questions for Class 10 Maths Chapter 14 Statistics Question No 2:
The abscissa of the point of intersection of the less than type and of the more than type cumulative frequency curves of a grouped data gives its
Option A : Mean
Option B : Median
Option C : Mode
Option D : All of Above
Show/Hide Answer Key
Option B : Median
MCQ Questions for Class 10 Maths Chapter 14 Statistics Question No 3:
One of the methods for determining mode is
Option A : Mode = 2 Median – 3 Mean
Option B : Mode = 3 Median – 2 Mean
Option C : Mode = 2 Mean – 3 Median
Option D : Mode = 3 Mean – 2 Median
Show/Hide Answer Key
Option B : Mode = 3 Median – 2 Mean
MCQ Questions for Class 10 Maths Chapter 14 Statistics Question No 4:
In a frequency distribution, the mid value of a class is 10 and the width of the class is 6. The lower limit of the class is
Option A : 6
Option B : 7
Option C : 8
Option D : 12
Show/Hide Answer Key
Option B : 7
MCQ Questions for Class 10 Maths Chapter 14 Statistics Question No 5:
For the following distribution :

the sum of lower limits of the median class and modal class is
Option A : 15
Option B : 25
Option C : 30
Option D : 35
Show/Hide Answer Key
Option B : 25
MCQ Questions for Class 10 Maths Chapter 14 Statistics Question No 6:
The algebraic sum of the deviations of a frequency distribution from its mean is always,
Option A : greater than zero
Option B : less than zero
Option C : zero
Option D : a non-zero number
Show/Hide Answer Key
Option C : zero
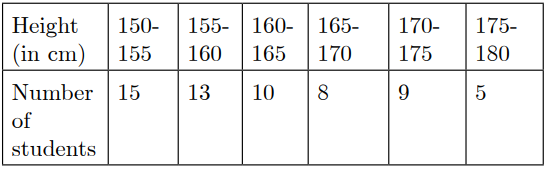
MCQ Questions for Class 10 Maths Chapter 14 Statistics Question No 7:
Consider the following frequency distribution of the heights of 60 students of a class.
The upper limit of the median class in the given data is
Option A : 165
Option B : 155
Option C : 150
Option D : 170
Show/Hide Answer Key
Option A : 165
MCQ Questions for Class 10 Maths Chapter 14 Statistics Question No 8:
Consider the following frequency distribution :
The difference of the upper limit of the median class and the lower limit of the modal class is
Option A : 0
Option B : 19
Option C : 20
Option D : 38
Show/Hide Answer Key
Option C : 20
MCQ Questions for Class 10 Maths Chapter 14 Statistics Question No 9:
Which of the following can not be determined graphically?
Option A : Mean
Option B : Median
Option C : Mode
Option D : None of Above
Show/Hide Answer Key
Option A : Mean
MCQ Questions for Class 10 Maths Chapter 14 Statistics Question No 10:
If the difference of mode and median of a data is 24, then the difference of median and mean is
Option A : 12
Option B : 24
Option C : 8
Option D : 36
Show/Hide Answer Key
Option A : 12
| CBSE Class 10 Maths Chapterwise MCQs |
|---|
| 1 : Real Numbers MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 2 : Polynomials MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 3 : Linear Equations MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 4 : Quadratic Equations MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 5 : Arithmetic Progression MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 6 : Triangles MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 7 : Coordinate Geometry MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 8 : Introduction to Trigonometry MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 9 : Application of Trigonometry MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 10 : Circles MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 11 : Constructions MCQ | 1 to 10 | 11 to 20 |
| 12 : Area Related to Circles MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 13 : Surface Area & Volume MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 14 : Statistics MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 15 : Probability MCQ | 1 to 10 | 11 to 20 | 21 to 30 | 31 to 40 | 41 to 50 |
| 16 : Previous Year Maths MCQs from CBSE Board Class 10 | 1 to 100 |