Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Test Prep 9 Grid Ins Questions with Answer Keys | SAT Online Course AMBiPi.
SAT 2022 Math Test Prep 9 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
Once an insect reaches its larval stage, its mass increases linearly for a short period and then slows down as it prepares to enter pupation. Suppose the larva of a certain species has an initial mass of 10 grams and grows linearly from t = 0 to t = 48 hours of its larval stage. If after 48 hours, the mass of the larva is 14 grams, what was its mass in grams at t = 6 hours?
Show/Hide Answer Key
Correct Answer: 10.5 or 21/2
Difficulty: Medium
Category: Heart of Algebra / Linear Equations
Strategic Advice: The keyword in this question is linear. In a real-world scenario that involves a constant rate of change, you almost always need to find the slope and the initial amount so you can write an equation. The question states that the initial mass of the larva was 10 grams, so all you need to do is find the slope.
Getting to the Answer: Write the information given in the question as ordered pairs (time, mass) so you can find the slope. At t = 0, the larva has a mass of 10 grams, so one pair is (0, 10). After 48 hours, the larva has a mass of 14 grams, so a second pair is (48, 14). Now, use the slope formula:
m = (y2 – y1)/(x2 – x1)
= (14 – 10)/(48 – 0) = 4/48 = 1/12
The equation is y = (1/12)x + 10, where y represents the mass of the larva after x hours. Substitute 6 for x to find the mass after 6 hours: (1/12)(6) + 10 = 6/12 + 10 = 10.5 grams.
SAT Math Practice Online Test Question No 2:
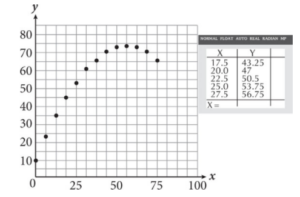
The maximum value of the data shown in the scatterplot occurs at x = 56.25. If the data is modeled using a quadratic regression and the correlation coefficient is 1.0, then what is the y-value when x = 90?
Show/Hide Answer Key
Correct Answer: 50.5
Difficulty: Hard
Category: Passport to Advanced Math / Scatterplots
Strategic Advice: This question requires a conceptual understanding of modeling data and properties of quadratic functions. When a regression model has a correlation coefficient of 1, it means that the model exactly fits the data. This tells you that you can use what you know about quadratic functions to answer the question.
Getting to the Answer: The graph of a quadratic function is symmetric concerning its axis of symmetry. The axis of symmetry occurs at the x-value of the vertex, which also happens to be where the maximum (or minimum) of the function occurs. The question tells you this value-it’s x = 56.25. Because x = 90 is 33.75 (90 – 56.25 = 33.75) units to the right of the axis of symmetry, you know that the y-value will be the same as the point that is 33.75 units to the left of the axis of symmetry. This occurs at x = 56.25 – 33.75 = 22.5. Read the y-value from the graphing calculator screenshot to find the answer, which is 50.5.
SAT Math Practice Online Test Question No 3:
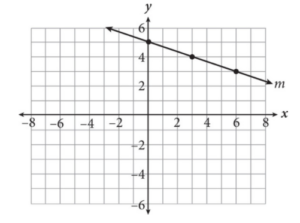
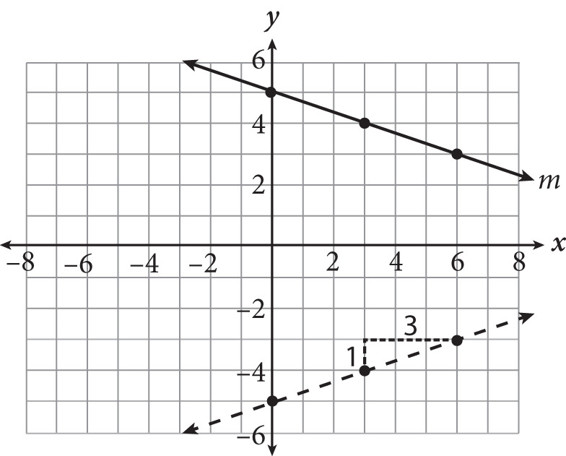
If line m shown above is reflected over the x-axis, what is the slope of the new line?
Show/Hide Answer Key
Correct Answer: 1/3 or .333
Difficulty: Easy
Category: Heart of Algebra / Linear Equations
Strategic Advice: When a grid is provided for you, take the time to draw a sketch on the grid.
Getting to the Answer: Sketch the reflection on the grid:
Use your sketch to count the vertical change and the horizontal change from one point to the next. Remember-slope has risen overrun. The slope of the reflected line is 1/3. Grid this in as 1/3 or .333.
SAT Math Practice Online Test Question No 4:
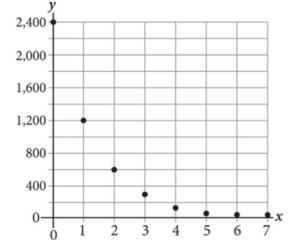
If an exponential function of the form h(x) = a(b)x is used to model the data shown in the graph above, what is the value of b?
Show/Hide Answer Key
Correct Answer: 1/2 or .5
Difficulty: Medium
Category: Passport to Advanced Math / Functions
Strategic Advice: Jot down the first few points and look for a pattern.
Getting to the Answer: The points are (0, 2,400), (1, 1,200), (2, 600), (3, 300), and so on. This means each y-value is half the previous value, so b, which is the decay rate, is 1/2. Grid this in as 1/2 or .5.
SAT Math Practice Online Test Question No 5:
If (1/4)x = 5 – (1/2)y, what is the value of x + 2y?
Show/Hide Answer Key
Correct Answer: 20
Difficulty: Medium
Category: Heart of Algebra / Linear Equations
Strategic Advice: Only one equation is given, and it has two variables. This means that you don’t have enough information to solve for either variable. Instead, look for the relationship between the variable terms in the equation and those in the expression that you are trying to find, x + 2y.
Getting to the Answer: First, move the y-term to the left side of the equation to make it look more like the expression you are trying to find. The expression doesn’t have fractions, so clear the fractions in the equation by multiplying both sides by 4. This yields the expression that you are looking for, x + 2y, so no further work is required-just read the value on the right-hand side of the equation. The answer is 20.
(1/4)x = 5 – (1/2)y
(1/4)x + (1/2)y = 5
4([1/4]x + [1/2]y) = 4(5)
x + 2y = 20
SAT Math Practice Online Test Question No 6:
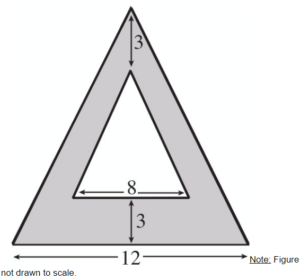
In the figure above, the area of the shaded region is 52 square units. What is the height of the larger triangle?
Show/Hide Answer Key
Correct Answer: 14
Difficulty: Hard Category: Additional Topics in Math / Geometry
Strategic Advice: The shaded region is the area of the larger triangle minus the area of the smaller triangle. Set up and solve an equation using the information from the figure. Before you grid in your answer, check that you answered the right question (height of the larger triangle).
Getting to the Answer: You don’t know the height of the smaller triangle, so call it h. You do know the area of the shaded region-it’s 52 square units.
Larger triangle: base = 12; height = h + 3 + 3
Smaller triangle: base = 8; height = h
Shaded area = large area – small area
52 = [(1/12)12 (h + 6)] – [(1/2)(8)(h)]
52 = 6(h + 6) – 4h
52 = 6h + 36 – 4h
52 = 2h + 36
16 = 2h
8 = h
The question asks for the height of the larger triangle, so the correct answer is 8 + 3 + 3 = 14.
SAT Math Practice Online Test Question No 7:
Given the function f(x) = (2/3)x – 5, what input value corresponds to an output of 3?
Show/Hide Answer Key
Correct Answer: 12
Difficulty: Medium
Category: Passport to Advanced Math / Functions
Strategic Advice: Understanding the language of functions will come in very handy on Test Day. For any function f(x), then x is the input value, and the output is the result after plugging in the input and simplifying.
Getting to the Answer: The question tells you that the output is 3 (not the input), so set the equation equal to 3 and solve for x.
3 = (2/3)x – 5
8 = (2/3)x
3 ⦁ 8 = 2x
24 = 2x
12 = x
SAT Math Practice Online Test Question No 8:
If a circle is given by the equation x2 + y2 + 10x – 4y = 20, what is its diameter?
Show/Hide Answer Key
Correct Answer: 14
Difficulty: Hard
Category: Additional Topics in Math / Geometry Strategic Advice:
When the equation of a circle is in the form (x – h)2 + (y – k)2 = r2, the r represents the length of the radius. To get the equation into this form, complete the squares.
Getting to the Answer: You already have an x2 and a y2 in the given equation and the coefficients of x and y are even, so completing the square is fairly straightforward-there are just a lot of steps. Start by grouping the xs and ys together. Then, take the coefficient of the x-term and divide it by 2, square it, and add it to the two terms with x-variables. Do the same with the y-term. Don’t forget to add these amounts to the other side of the equation as well. This creates a perfect square of x-terms and y-terms, so take the square root of each.
x2 + y2 + 10x – 4y = 20
x2 + 10x + y2 – 4y = 20
(x2 + 10x + 25) + (y2 – 4y + 4) = 20 + 25 + 4
(x + 5)2 + (y – 2)2 = 49
The equation tells you that r2 = 49, which means that the radius is 7 and the diameter is twice that, or 14.
SAT Math Practice Online Test Question No 9:
A right triangle has leg lengths of 18 and 24 and a hypotenuse of 15n. What is the value of n?
Show/Hide Answer Key
Correct Answer: 2
Difficulty: Medium
Category: Additional Topics in Math / Geometry
Strategic Advice: Take a second to think about this question before you go right to the Pythagorean theorem. Remember that the PSAT often tests your knowledge of “shortcut” information.
Getting to the Answer: You could use the Pythagorean theorem to solve this, but it will save valuable time on Test Day if you recognize that this question is testing your knowledge of Pythagorean triples. The triangle is a right triangle with leg lengths of 18 and 24, which, when divided by 6, are in the proportion 3:4. This means that the triangle is a scaled-up 3:4:5 right triangle with a scale factor of 6. To keep the same proportion, the hypotenuse must be 5 × 6 = 30. For 15n to equal 30, n must be 2.
SAT Math Practice Online Test Question No 10:
If the product of (3 + √-16)(1 – √-36) is written as a complex number in the form a + bi, what is the value of a? (Note: √-1)
Show/Hide Answer Key
Correct Answer: 27
Difficulty: Hard
Category: Additional Topics in Math / Imaginary Numbers
Strategic Advice: Each of the factors in this product has two terms, so they behave like binomials. This means you can use FOIL to find the product. To avoid messy numbers, simplify the two radicals first using the definition of i.
Getting to the Answer: Write each of the numbers under the radicals as a product of -1 and the number, take the square roots, and then FOIL the resulting expressions:
(3 + √-16)(1 – √-36)
= (3 + [√16 x √-1]) (1 – [√36 x (-1)])
= (3 + 4i)(1 – 6i) = 3 – 18i + 4i – 24i
= 3 – 14i – 24(-1)
= 3 – 14i + 24
= 27 – 14i