Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Practice Test 3 Grid Ins Questions with Answer Keys | SAT Online Course AMBiPi.
SAT 2022 Math Practice Test 3 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
Let If (x2 + x – 6)/(x2 – 8x + 12) = 4, what is the value of x?
Show/Hide Answer Key
Correct Answer: 9
Factor the numerator and the denominator into (x – 2)(x + 3)/(x – 2)(x – 6) = 4.
The (x – 2) cancels out of the top and bottom to leave (x + 3)/(x – 6) = 4.
Multiply both sides by (x – 6) to get x + 3 = 4x – 24.
Subtract x from both sides: 3 = 3x – 24. Add 24 to both sides: 27 = 3x. Divide by 3 to get x = 9.
SAT Math Practice Online Test Question No 2:
If Alexandra pays $56.65 for a table, and this amount includes a tax of 3% on the price of the table, what is the amount, in dollars, that she pays in tax? (Disregard the dollar sign when gridding your answer.)
Show/Hide Answer Key
Correct Answer: 1.65
The best way to approach this problem is to set up an equation.
There is some price such that if you add 3% of the price to the price itself, you get $56.65.
This means that you can set up an equation: x + 3% of x = 56.65, or x + 0.03x = 56.65. Now you can just solve for x, and you get the original price, which was $55. Subtract this from $56.65 to get the tax of $1.65.
SAT Math Practice Online Test Question No 3:
A garden, measuring 10 feet by 12 feet, contains individual plots that measure 1 foot by 1 foot. 30% of the plots contain bell peppers, 30% contain cherry tomatoes, 25% contain squash, and the remaining 15% contain eggplants. Each bell pepper plot produces 2 bell peppers every 5 days, a tomato plot produces 4 cherry tomatoes every 6 days, a squash plot produces 1 squash every 15 days, and an eggplant plot produces 3 eggplants every 10 days.
An unusually warm and wet month causes the monthly production of eggplants to double. What is the daily average number of eggplants produced in the garden during a 30-day month at the new rate?
Show/Hide Answer Key
Correct Answer: 10.8
During a normal month, each eggplant plot produces 3 eggplants every 10 days. Therefore, if the production were to double, each plot would produce 6 eggplants every 10 days.
Given that the garden measures 10 feet by 12 feet and each plot is one foot by one foot, there are 10 × 12 = 120 total plots, 15% of which are eggplant plots. Therefore, there are 120 × 0.15 = 18 eggplant plots.
Calculate the total number of eggplants produced in 10 days as 18 × 6 = 108. In a 30-day month, there are three 10-day periods, so the entire garden would produce 108 × 3 = 324 total eggplants. To find the daily average production, divide 324 by 30 to get an average of 10.8 eggplants each day.
SAT Math Practice Online Test Question No 4:
The parabola y = –x2 + 5x + 6 is intersected by the line y = (-1/2)x + 12. What is the y-coordinate of the intersection closest to the x-axis?
Show/Hide Answer Key
Correct Answer: 10
To solve the problem without a graphing calculator, set the two equations equal to each other: –x2 + 5x + 6 = x + 12.
Multiply the entire equation by 2 to get -2x2 + 10x + 12 = –x + 24. Rewrite the equation so that it equals 0, so it becomes -2x2 + 11x – 12 = 0. Multiply the entire equation by -1 to get 2x2 – 11x + 12 = 0. Factor the quadratic to get (2x – 3)(x – 4) = 0.
Solve for the two possible values of x: If 2x – 3 = 0, then x = 3/2, and if x – 4 = 0, then x = 4. Because the slope of the line is negative, the x-value of the point that is farthest to the right along the x-axis must also be closer to the x-axis.
Plug 4 in for x in the second equation to get y = (-1/2)(4) + 12 = -2 + 12 = 10. The correct answer is 10.
SAT Math Practice Online Test Question No 5:
If 9 > 3v – 3, what is the greatest possible integer value of v?
Show/Hide Answer Key
Correct Answer: 3
Solve the equation for v.
Take 9 > 3v – 3 and add 3 to both sides to get 12 > 3v. Now divide both sides by 3 to find that 4 > v. Therefore, the largest integer that v could be is 3. Grid in 3.
SAT Math Practice Online Test Question No 6:
Professor Malingowski, a chemist and teacher at a community college, is organizing his graduated cylinders in the hopes of keeping his office tidy and setting a good example for his students. He has beakers with diameters, in inches, of 1/2,3/4,4/5,1 and 5/4. Professor Malingowski notices one additional cylinder lying on the ground, and can recall certain facts about it, but not its actual diameter. If he knows that the value of the additional graduated cylinder’s diameter, x, will not create any modes and will make the mean of the set equal to 5/6, what is the value of the additional cylinder’s diameter?
Show/Hide Answer Key
Correct Answer: 0.7
If the mean of the new set is 5/6, then the sum of the diameters of the cylinders divided by the number of cylinders must equal 5/6.
Set up the equation: 5/6 = (1/2 + 3/4 + 4/5 + 1 + 5/4 + x)/6 , where x is the unknown cylinder.
Multiply both sides by 6 to simplify: 5 = 1/2 + 3/4 + 4/5 + 1 + 5/4 + x.
5 = 43/10 + x. Subtract 43/10 from both sides and you get 7/10.
SAT Math Practice Online Test Question No 7:
A standard parabola in the x,y-coordinate plane intersects the x-axis at (5, 0) and (-5, 0). What is the value of the x-coordinate of this parabola’s line of symmetry?
Show/Hide Answer Key
Correct Answer: 0
If a parabola intersects the x-axis at the points (5,0) and (-5,0), it must be symmetric about the x-axis and centered at x = 0.
The x-coordinate of its vertical axis of symmetry must then be 0.
SAT Math Practice Online Test Question No 8:
What number divided by two is equal to that same number minus 15?
Show/Hide Answer Key
Correct Answer: 30
Translate English to math. “What number divided by two is equal to that same number minus 15?” can be written as an equation, with x representing the missing number: x/2 = x – 15.
Add 15 to both sides of the equation to get x/2 + 15 = x. Subtract x/2 from both sides to get 15 = x/2. Multiply both sides by 2 to get x = 30.
SAT Math Practice Online Test Question No 9:
In the equation 3x2 – 16x = -20, what is one possible value of x?
Show/Hide Answer Key
Correct Answer: 2 or 10/3
There are a few different ways to approach this question.
Since the calculator is permitted on this section of the test, you can put the equation into the standard ax2 + bx + c = 0 form and plug that equation into the “y =” button on your graphing calculator. The equation, once rearranged, is 3x2 – 16x + 20 = 0. You can trace the graph or use the “calc” feature to calculate the zeroes, which are the same as the values of x. Doing so will yield values of x = 2 and x = 3.33.
Alternatively, you can factor the equation the long way or use the quadratic formula, (-b±√(b²-4ac))/(2a). In this equation, a = 3, b = -16, and c = 20. Plugging those values into the equation, you get (-(-16)±√((-16)²-4(3)(20))/(2(3) = (16 ± √16)/6 = (16 ± 4)/6. Therefore, the solutions are (16 + 4)/6 = 20/6 = 10/3 and (16 – 4)/6 = 12/6 = 2. Either value (10/3 or 2) is a valid answer.
SAT Math Practice Online Test Question No 10:
The chart below shows the population distribution for the 2,400 occupants of the city of Centre Hill.
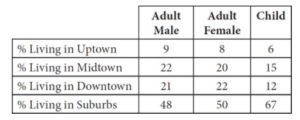
If there are an equal number of adults and children, and adult females outnumber adult males by 200, what is the sum of the women living uptown and the children living in the suburbs of Centre Hill?
Show/Hide Answer Key
Correct Answer: 860
The question states that there are 2,400 total inhabitants of Centre Hill, so if there are an equal number of adults and children, then there are 1,200 of each.
Since there are 200 more adult females than adult males, you can set up two equations: f + m = 1,200 and f = m + 200. You can rewrite the second equation by subtracting m from both sides: f – m = 200.
Next, stack and add the two equations as follows: [(f + m = 1,200) + (f – m = 200)] = (2f = 1,400).
Divide both sides of the equation by 2 to determine that f = 700. The number of women living uptown is therefore 8% of 700: (8/100)700 or (0.08)(700) = 56. The number of children living in the suburbs is 67% of 1,200: (67/100)(1,200) or (0.67)(1,200) = 804. The sum of these two figures is 56 + 804 = 860.



