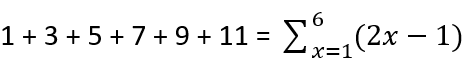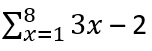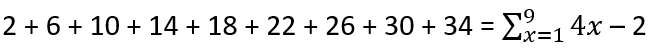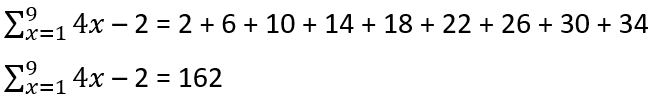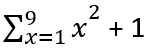Hi students, welcome to Amans Maths Blogs (AMBiPi). Sigma notation is a compact manner of writing a sum of multiple terms. Sigma notation is generally the notation of the summation. A summation is a brief approach for writing a long sequence or a large number of terms. It is commonly utilized in mathematics, as the use of summation is vital in calculus.
What is a Sigma Notation?
Sigma notation is a compact manner of writing a sum of multiple terms. The sigma notation is a symbol used to add any sort of integers in a sequence. It’s a process of adding up a number of items. This notation is used in the summation. The summation means the sum of all the terms in the sigma notation from initial to final values. In simple words, Summation or sigma notation can be used to represent a series in a brief format. The sum is represented by the Greek capital letter ∑.
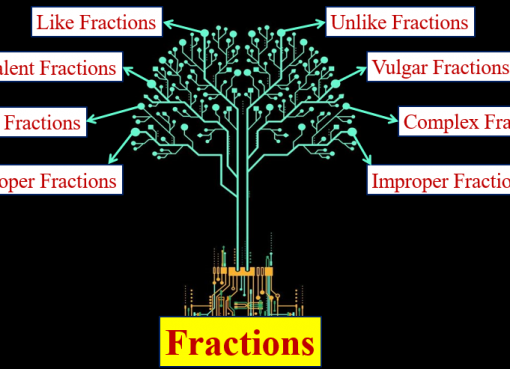
A sum is being taken, as indicated by the Σ (sigma). The variable x is referred to as the sum’s index. The upper and lower bounds of the summation are the values at the top and bottom of the sigma Σ.
For example, we can write a series such as 1 + 3 + 5 + 7 + 9 + 11 in sigma notation, we use the Σ sign and take the initial and final value of the series as initial can be zero or one and the final value is the total numbers of the terms in a series.
Similarly, we can also take the sigma notation of the series of even numbers such as 2 + 4 + 6 + 8 + 10 + 12 as,
How to Calculate Sigma Notation?
There are two calculations of sigma notation. Converting a series in sigma notation and converting a sigma notation in series. You can use sigma notation calculator to perform simple summation and sigma notation summation.
Sequence to Sigma Notation
When a sequence is given with an equal difference among the terms then we can apply the sigma notation.
Example 1:
Convert the given series in sigma notation.
1 + 4 + 7 +10 + 13 + 16 + 19 + 22
Solution:
Step 1: Write the series.
1 + 4 + 7 +10 + 13 + 16 + 19 + 22
Step 2: Identify the common difference between the terms.
The common difference = 3
Step 3: Identify the function that gives the series by applying the values.
Function = 3x – 2
Step 4: Write the sigma notation with the above function, while the upper limit is n = 8.
Step 5: write the series with the result.
Example 2:
Convert the given series in sigma notation.
2 + 6 + 10 + 14 + 18 + 22 + 26 + 30 + 34
Solution:
Step 1: Write the series.
1 + 4 + 7 +10 + 13 + 16 + 19 + 22
Step 2: Identify the common difference between the terms.
The common difference = 4
Step 3: Identify the function that gives the series by applying the values.
Function = 4x – 2
Step 4: Write the sigma notation with the above function, while the upper limit is n = 8.
Step 5: write the series with the result.
Sigma Notation to Series
When a sequence is given in the sigma notation, we open that notation by putting the limits to get the series.
Example 1:
Evaluate :
Step 1: Write the function.
4x – 2
Step 2: Identify the values from initial to final.
1 to 9 = 1, 2, 3, 4, 5, 6, 7, 8, 9
Step 3: Put the limit values one by one in the given function.
At x = 1,
4x – 2 = 4(1) – 2 = 4 – 2 = 2
At x = 2,
4x – 2 = 4(2) – 2 = 8 – 2 = 6
At x = 3,
4x – 2 = 4(3) – 2 = 12 – 2 = 10
At x = 4,
4x – 2 = 4(4) – 2 = 16 – 2 = 14
At x = 5,
4x – 2 = 4(5) – 2 = 20 – 2 = 18
At x = 6,
4x – 2 = 4(6) – 2 = 24 – 2 = 22
At x = 7,
4x – 2 = 4(7) – 2 = 28 – 2 = 26
At x = 8,
4x – 2 = 4(8) – 2 = 32 – 2 = 30
At x = 9,
4x – 2 = 4(9) – 2 = 36 – 2 = 34
Step 4: Write the series and find the sum of series.
Example 2:
Evaluate :
Step 1: Write the function.
x2 + 1
Step 2: Identify the values from initial to final.
1 to 9 = 1, 2, 3, 4, 5, 6, 7, 8, 9
Step 3: Put the limit values one by one in the given function.
At x = 1,
x2 + 1 = (1)2 + 1 = 1 + 1 = 2
At x = 2,
x2 + 1 = (2)2 + 1 = 4 + 1 = 5
At x = 3,
x2 + 1 = (3)2 + 1 = 9 + 1 = 10
At x = 4,
x2 + 1 = (4)2 + 1 = 16 + 1 = 17
At x = 5,
x2 + 1 = (5)2 + 1 = 25 + 1 = 26
At x = 6,
x2 + 1 = (6)2 + 1 = 36 + 1 = 37
At x = 7,
x2 + 1 = (7)2 + 1 = 49 + 1 = 50
At x = 8,
x2 + 1 = (8)2 + 1 = 64 + 1 = 65
At x = 9,
x2 + 1 = (9)2 + 1 = 81 + 1 = 82
Step 4: Write the series.
Summary
Sigma notation is a compact manner of writing a sum of multiple terms. The sigma notation is a symbol used to add any sort of integers in a sequence. This notation is widely used in sequences. Sigma notation is used to reduce the difficulty of writing a large number of terms.