CBSE Class 8 Maths Visualizing Solid Shapes Notes And Questions
Hi students, welcome to Amans Maths Blogs (AMB). On this page, you will get the short notes and important question of CBSE Class 8 Maths Visualizing Solid Shapes. These short notes and important questions are taken from the NCERT text books and other books. If you want to get the NCERT Solution for class 8 Maths Visualizing Solid Shapes Chapter, then click here. If you need sample questions based on visualizing solid shapes for practice, then you are at right place.
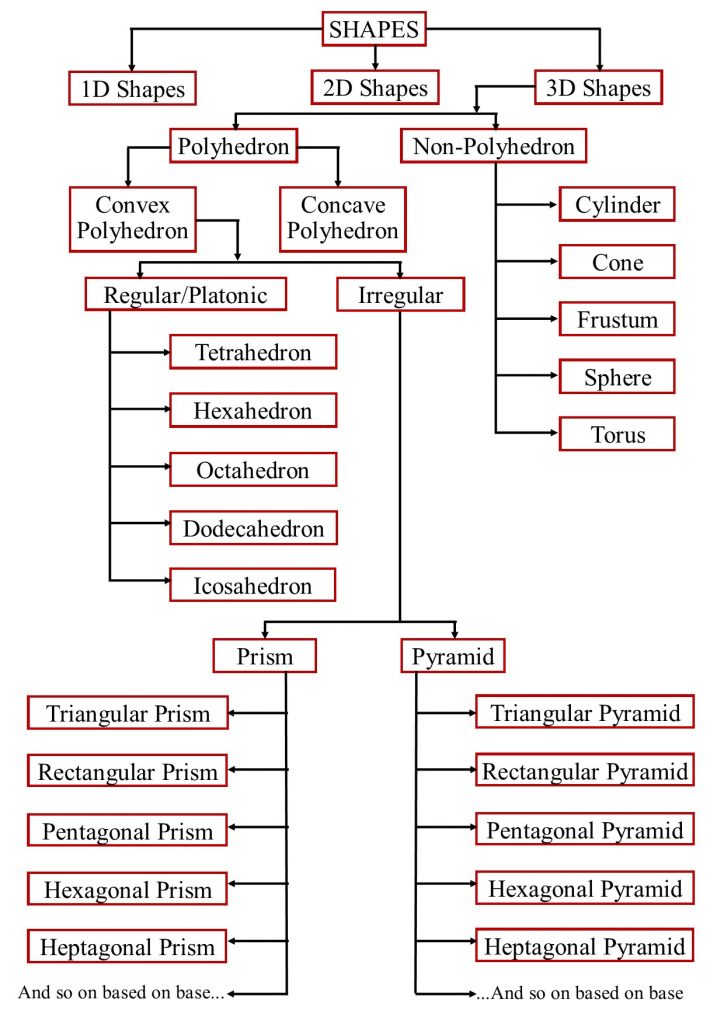
Shapes
Geometrical figures are known as shapes. There are three types of shapes.
One Dimensional (1D) shape: Line
Two Dimensional (2D) shape: Rectangle cancel etc.
Three Dimensional (3D) shape: Polyhedron, Non-Polyhedrons etc.
Polyhedron
A solid shape bounded by the polygons is called Polyhedron. The plural word for polyhedron are Polyhedron, polyhedrons or polyhedral. Polyhedrons are described by three components. This is studied in CBSE Class 8 Maths Visualizing Solid Shapes.
Faces: polygons forming a polyhedron are known as faces.
Edges: the line segments formed by the intersection of two faces of a polyhedron known as Edges.
Vertices: the points of intersection of edges of a polyhedron are known as vertices.
Figure
Euler’s Formula
A formula which relates the number of faces (F)the number of vertices (V) and the number of edges (E) of a polyhedron is known as Euler’s Formula. Thus, F + V = E + 2 or F + V – E = 2.
In cube, F = 6, V = 8, E = 12. Thus, F + V – E = 6 + 8 -12 = 2 Hence, cube is a polyhedron.
The Euler’s formula is only for polyhedrons, not for non- polyhedrons like cylinder cone etc.
Non-Polyhedron
The solids which are not made of polygons are known as Non-polyhedrons.
Example:
Figure
Now polyhedrons are of two types: convex polyhedrons and concave polyhedrons.
Convex & Concave Polyhedrons
If the line segment joining any two ports on the surfaces of a polyhedron entirely lies aside or on the polyhedron, then it is said to be a convex polyhedron otherwise it is known as concave polyhedron. In CBSE Class 8 Maths Visualizing Solid Shapes, this is very important chapters.
Figure 2
Regular & Irregular Polyhedrons
A polyhedron is a regular polyhedron if its faces are formed by the regular polygons and the same number of meet at each vertex. otherwise, it is an irregular polyhedron.
Figure 2
Prism
A prism is a solid whose faces are parallelograms and the ends are congruent parallel two Dimensional’s shapes A prism has both and congruent polygon (two dimensional figures). Now, the prism are of two types. In CBSE Class 8 Maths Visualizing Solid Shapes, we need to develop the basic terminology regarding Prism.
Right Prism & Oblique Prism
A prism whose both ends polygons are parallel to each other or the lateral faces are perpendicular to each polygon is known as Right Prism otherwise it is an Oblique Prism.
Triangular Prism
A prism which has triangles in both ends is known as Triangular Prism.
Here, F = 5, V = 6 and E = 9. Euler’s Formula: F + V – E = 5 + 6 – 9 = 2
Rectangular Prism
A prism which has rectangle in both ends is known as Rectangular Prism. Thus, the cubiod is also known as Rectangular Prism.
Here, F = 6, V = 8 and E = 12. Euler’s Formula: F + V – E = 6 + 8 – 12 = 2
Parallelopiped
A prism has a parallelopiped as its base is called Parallelopiped. In this chapter, CBSE Class 8 Maths Visualizing Solid Shapes, is starting concepts of Parallelopiped.
Here, F = 6, V = 8 and E = 12. Euler’s Formula: F + V – E = 6 + 8 – 12 = 2
Pyramid
A Pyramid is a polyhedron whose base is a polygon and other faces are triangle meeting at a common vertex is known as Pyramid. In other words, if all the corners of a polygon are joined to a point not laying in the plane, then the obtained polyhedron is known as Pyramid.
Triangular Pyramid
A Pyramid which has a triangle in its base is known as Triangular Pyramid.
Here, F = 4, V = 4 and E = 6. Euler’s Formula: F + V – E = 4 + 4 – 6 = 2
Rectangular Pyramid
A Pyramid which has a rectangle in its base is known as Rectangular Pyramid.
Here, F = 5, V = 5 and E = 8. Euler’s Formula: F + V – E = 5 + 5 – 8 = 2
Square Pyramid
A Pyramid which has a square in its base is known as Square Pyramid.
Here, F = 5, V = 5 and E = 8. Euler’s Formula: F + V – E = 5 + 5 – 8 = 2
Platonic Solids
A solid is a regular convex polyhedron in which each face is the same regular polygon and the same number of polygons meet at each vertex is known as Platonic Solids. In Platonic solid, the sum of all angles at a vertex is less than 360 degree. There are five Platonic solids.
Tetrahedrons
A triangular pyramid in which all the faces are equilateral triangles is called Tetrahedrons. In this, three equilateral triangles meet at each other is 3 x 60 = 180 degree < 360 degree.
Here, F = 4, V = 4 and E = 6. Euler’s Formula: F + V – E = 4 + 4 – 8 = 2
Octahedrons
An Octahedron is a solid in which all the faces are equilateral triangles. In this, four equilateral triangles meet at each other vertex. Thus, the sum of all angles at each vertex is 4 x 60 = 240 degree < 360 degree.
Here, F = 8, V = 6 and E = 12. Euler’s Formula: F + V – E = 8 + 6 – 12 = 2
Icosahedrons
An Icosahedron is a solid in which all the faces are equilateral triangles. In this case, five equilateral triangles meet at each vertex. Thus, the sum of all angles at each vertex is 5 x 60 = 300 degree < 360 degree.
Here, F = 20, V = 12 and E = 30. Euler’s Formula: F + V – E = 20 + 12 – 30 = 2
Hexahedrons
A hexahedron is a solid in which all the faces are square. In this case, three squares meet at each vertex. Thus, the sum of all angles at each vertex is 3 x 90 = 270 degree < 360 degree.
Here, F = 6, V = 8 and E = 12. Euler’s Formula: F + V – E = 6 + 8 – 12 = 2
Hence, a cube is also known as Hexahedrons.
Dodecahedrons
A Dodecahedron is a solid in which all the faces are pentagons. In this, three pentagons meet at each vertex. Thus, the sum of all angles at each vertex is 3 x 108 = 324 degree < 360 degree.
Here, F = 12, V = 20 and E = 30. Euler’s Formula: F + V – E = 12 + 20 – 30 = 2.
Visualizing of Solid Shapes
The visualization of solid shape is done by sketching the 3-D figures on the plane paper as the representation of 2D figures. The representation of solid object 3D figures into 2D figures on plane paper is done by two types of sketch techniques known as Oblique Sketching and Isometric Sketching.
In oblique sketching, we draw the face or front of 3D objects by drawing 45 degree angle to render the third dimension on plane. In isometric sketching, we draw the edges of 3D objects by drawing 30 degree angle to render the third dimension on dotted paper.
Net Diagrams
A geometrical net diagram is a two dimensional shape that can be folded to form a three dimensional solid shapes. A solid may have different nets.