Trigonometry Formulas
Hi students, welcome to Amans Maths Blogs (AMB). On this post, you will get the all the Trigonometry Formulas. It will help you to solve the trigonometry questions. This Trigonometry Formulas is very useful for in the revision before the school exams or competitive exams like SSC, IBPS, CAT, NTSE etc. This is in the form PDF file so you can download it your mobile/laptop and save this PDF file permanently.
Trigonometry Formulas : Degree To Radian
To convert an angle in degree into radian, we need to multiply π/180 to the degree.
For example: 30 degree = 30 x π/180 = π/6 radian.
Trigonometry Formulas : Radian To Degree
To convert an angle in radian into degree, we need to multiply 180/π to the degree.
For example: π/6 radian = π/6 x 180/π = 30 degree.
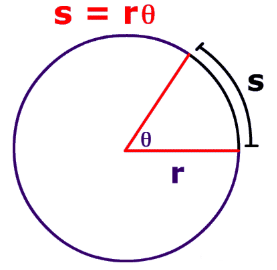
Trigonometry Formulas : Arc Length & Angle of Sector of Circle
If an arc makes an angle θ (in radian) at the center of a circle whose radius is r, then the length of an arc of the arc is s = rθ. Hence, we can say that the angle θ = s/r radian.
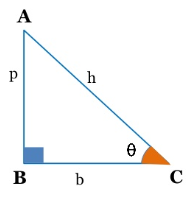
Trigonometry Formulas : Pythagorean Theorem
In a right angled triangle, the sum of the square of its perpendicular and the square of its base is equal to the square of the hypotenuse. This is known as Pythagorean theorem.
In the figure below, ABC is a right angled triangle with right angle at B. In this triangle, the side opposite to the right angle B is the hypotenuse (h = AC), the side opposite to the angle ACB = θ is the perpendicular (p = AB) and the side BC is the base (b).
Thus, according to the Pythagorean theorem p2 + b2 = h2.
We can also write it as p2 = h2 – b2 or b2 = h2 – p2.
Trigonometry Formulas : Trigonometric Ratios
In trigonometry, we study the relation between the sides and angles of a right triangle. For this, six trigonometric ratios are defined as below.
1. Sine of θ is denoted as sinθ and it is the ratio of perpendicular (p) and hypotenuse (h). It means,
sinθ = p/h = AB/AC.
2. Cosine of θ is denoted as cosθ and it is the ratio of base (b) and hypotenuse (h). It means,
cosθ = b/h = BC/AC.
3. Tangent of θ is denoted as tanθ and it is the ratio of perpendicular (p) and base (b). It means,
tanθ = p/b = AB/BC.
4. Cosecant of θ is denoted as cosecθ or cscθ and it is the ratio of hypotenuse (h) and perpendicular (p). It means,
cosecθ or cscθ = h/p = AC/AB.
5. Secant of θ is denoted as secθ and it is the ratio of hypotenuse (h) and base (b). It means,
secθ = h/b = AC/BC.
6. Cotangent of θ is denoted as cotθ and it is the ratio of base (b) and hypotenuse (h). It means,
cotθ = b/p = BC/AB.
Read : Trigonometry Ratios Questions And Answer
Trigonometry Formulas : Quotient Identities
Since sinθ = p/h, cosθ = b/h and tanθ = p/b, then tanθ = (p/h) / (b/h). Thus,
tanθ = sinθ / cosθ.
Since sinθ = p/h, cosθ = b/h and cotθ = b/p, then cotθ = (b/h) / (p/h). Thus,
cotθ = cosθ / sinθ.
Trigonometry Formulas : Reciprocal Identities
Since sinθ = p/h and cosecθ = h/p, then
sinθ x cosecθ = 1 or sinθ = 1/ cosecθ and cosecθ = 1/ sinθ.
Since cosθ = b/h and secθ = h/b, then
cosθ x secθ = 1 or cosθ = 1/ secθ and secθ = 1/ cosθ.
Since tanθ = p/b and cotθ = b/p, then
tanθ x cotθ = 1 or tanθ = 1/ cotθ and cotθ = 1/ tanθ.
Trigonometry Formulas : Trigonometric Identities
Using Pythagorean theorem p2 + b2 = h2 and the basic definition of trigonometric ratios, we get three trigonometric identities as below.
sin2θ + cos2θ = 1
sec2θ – tan2θ = 1
cosec2θ – cot2θ = 1
Using a2 – b2 = (a + b)(a – b) in sec2θ – tan2θ = 1, we get (secθ + tanθ)(secθ – tanθ) = 1. Thus, we get results as
secθ + tanθ = 1 / (secθ – tanθ)
and
secθ – tanθ = 1 / (secθ + tanθ),
where θ nπ + π/2
Using a2 – b2 = (a + b)(a – b) in cosec2θ – cot2θ = 1, we get (cosecθ + cotθ)(cosecθ – cotθ) = 1. Thus, we get results as
cosecθ + cotθ = 1 / (cosecθ – cotθ)
and
cosecθ – cotθ = 1 / (cosecθ + cotθ),
where θ nπ.
Read : Trigonometry Identities Questions And Answer
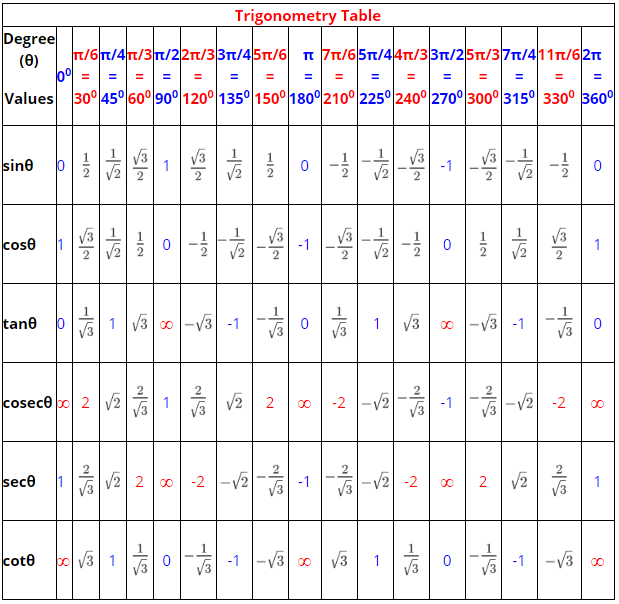
Trigonometry Formulas : Trigonometric Table
There are some specific trigonometric values of certain angles which are given below in trigonometric table.
Read : Trigonometry Table Questions And Answer
Trigonometry Formulas : Trigonometric Values
There are also trigonometric values of some important angles other than 0, 30, 45, 60, 90, 120, 135, 150, 180, 210, 225, 240, 270, 300, 315, 330 and 360 degrees as given in above trigonometric table.
1. sin15o = cos75o = ,
2. cos15o = sin75o = ,
3. tan15o = cot75o = ,
4. cot15o = tan75o = ,
5. sin22.5o = cos67.5o = ,
6. cos22.5o = sin67.5o = ,
7. tan22.5o = ,
8. cot22.5o = ,
9. sin18o = cos72o = ,
10. cos18o = sin72o = ,
11. sin36o = cos54o = ,
12. cos36o = sin54o = ,
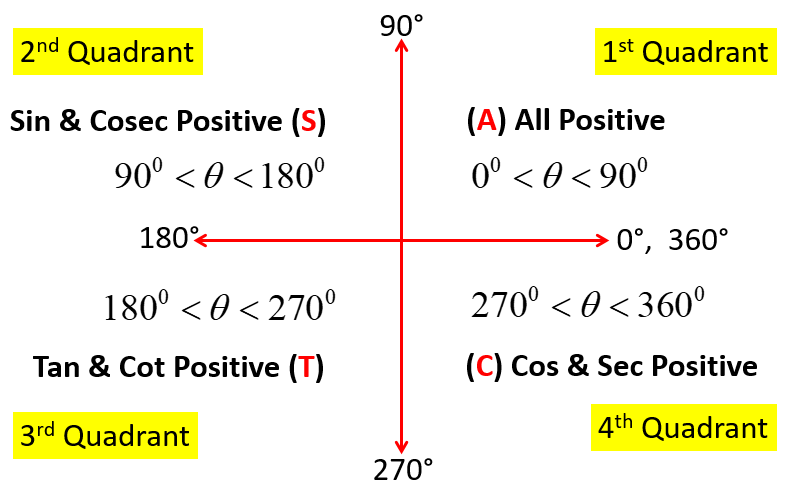
Trigonometry Formulas : Sign of Trigonometric Ratios
The sign of the trigonometric ratios (sinθ, cosθ, tanθ, cosecθ, secθ, cotθ) depends on the angle θ in which it lies in the quadrants. For this, we use the concept of ASTC rule.
A is at the first position (means 1st quadrant) in ASTC which means All (A means All). It means all the trigonometric ratios of an angle θ in first quadrant (0o < θ < 90o) are positive.
S is at the second position (means 2nd quadrant) in ASTC which means Sin and its reciprocal Cosec (S means Sin & Cosec). It means only Sin and Cosec of an angle θ in second quadrant (90o < θ < 180o) are positive and other remaining trigonometric ratios (cosθ, tanθ, secθ, cotθ) are negative.
T is at the third position (means 3rd quadrant) in ASTC which means Tan and its reciprocal Cot (T means Tan & Cot). It means only Tan and Cot of an angle θ in third quadrant (180o < θ < 270o) are positive and other remaining trigonometric ratios (sinθ, cosθ, cosecθ, secθ) are negative.
C is at the fourth position (means 4th quadrant) in ASTC which means Cos and its reciprocal Sec (C means Cos & Sec). It means only Cos and Sec of an angle θ in fourth quadrant (270o < θ < 360o) are positive and other remaining trigonometric ratios (sinθ, tanθ, cosecθ, cotθ) are negative.
Trigonometry Formulas : Allied Angles Formula
The angles 90o θ, 180o
θ, 270o
θ and 360o
θ are knwon as allied angles. The value of trigonometric ratios of these allied angles is according to the ASTC rule as discussed above.
Here, another rule is also used known as the odd and even multiplications of 90o.
90o = 1 x 90o and 270o = 3 x 90o are the odd multiplication of 90o. In this case, the trigonometric ratios are changed in pairs. It means
sin is changed to cos and cos is changed to sin
tan is changed to cot and cot is changed to tan
cosec is changed to sec and sec is changed to cosec
180o = 2 x 90o and 360o = 4 x 90o are the even multiplication of 90o. In this case, the trigonometric ratios are NOT changed. It means
sin remains sin and cos remains cos
tan remains tan and cot remains cot
cosec remains cosec and sec remains sec
Now, the allied angle (90o – θ) is in the first quadrant and 90o = 1 x 90o is odd multiplicative of 90o, so all the trigonometric ratios of (90o – θ) will be positive and all the trigonometric ratios are changed according to discussed above.
Hence, we conclude that
sin(90o – θ) = +cosθ
cos(90o – θ) = +sinθ
tan(90o – θ) = +cotθ
cosec(90o – θ) = +secθ
sec(90o – θ) = +cosecθ
cot(90o – θ) = +tanθ
The allied angle (90o + θ) is in the second quadrant and 90o = 1 x 90o is odd multiplicative of 90o, so the trigonometric ratios sin and cosec of (90o + θ) will be positive and other will be negative and all the trigonometric ratios are changed in pairs.
Hence, we conclude that
sin(90o + θ) = +cosθ
cos(90o + θ) = -sinθ
tan(90o + θ) = -cotθ
cosec(90o + θ) = +secθ
sec(90o + θ) = -cosecθ
cot(90o + θ) = -tanθ
The allied angle (180o – θ) is in the second quadrant and 180o = 2 x 90o is even multiplicative of 90o, so the trigonometric ratios sin and cosec of (180o – θ) will be positive and other will be negative and all the trigonometric ratios remain same.
Hence, we conclude that
sin(180o – θ) = +sinθ
cos(180o – θ) = -cosθ
tan(180o – θ) = -tanθ
cosec(180o – θ) = +cosecθ
sec(180o – θ) = -secθ
cot(180o – θ) = -cotθ
The allied angle (180o + θ) is in the third quadrant and 180o = 2 x 90o is even multiplicative of 90o, so the trigonometric ratios tan and cot of (180o + θ) will be positive and other will be negative and all the trigonometric ratios remain same.
Hence, we conclude that
sin(180o + θ) = -sinθ
cos(180o + θ) = -cosθ
tan(180o + θ) = +tanθ
cosec(180o + θ) = -cosecθ
sec(180o + θ) = -secθ
cot(180o + θ) = +cotθ
The allied angle (270o – θ) is in the third quadrant and 270o = 3 x 90o is odd multiplicative of 90o, so the trigonometric ratios tan and cot of (270o – θ) will be positive and other will be negative and all the trigonometric ratios are changed in pairs.
Hence, we conclude that
sin(270o – θ) = -cosθ
cos(270o – θ) = -sinθ
tan(270o – θ) = +cotθ
cosec(270o – θ) = -secθ
sec(270o – θ) = -cosecθ
cot(270o – θ) = +tanθ
The allied angle (270o + θ) is in the fourth quadrant and 270o = 3 x 90o is odd multiplicative of 90o, so the trigonometric ratios cos and sec of (270o + θ) will be positive and other will be negative and all the trigonometric ratios are changed in pairs.
Hence, we conclude that
sin(270o + θ) = -cosθ
cos(270o + θ) = +sinθ
tan(270o + θ) = -cotθ
cosec(270o + θ) = -secθ
sec(270o + θ) = +cosecθ
cot(270o + θ) = -tanθ
The allied angle (360o – θ) is in the fourth quadrant and 360o = 4 x 90o is even multiplicative of 90o, so the trigonometric ratios cos and sec of (360o – θ) will be positive and other will be negative and all the trigonometric ratios remain same.
Hence, we conclude that
sin(360o – θ) = -sinθ
cos(360o – θ) = +cosθ
tan(360o – θ) = -tanθ
cosec(360o – θ) = -cosecθ
sec(360o – θ) = +secθ
cot(360o – θ) = -cotθ
The allied angle (360o + θ) is again in the first quadrant and 360o = 4 x 90o is even multiplicative of 90o, so all the trigonometric ratios of (360o + θ) will be positive and other will be negative and all the trigonometric ratios remain same.
Hence, we conclude that
sin(360o + θ) = +sinθ
cos(360o + θ) = +cosθ
tan(360o + θ) = +tanθ
cosec(360o + θ) = +cosecθ
sec(360o + θ) = +secθ
cot(360o + θ) = +cotθ
Read : Trigonometry Allied Angles Questions And Answer