Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Practice Questions Test 15 Grid Ins Questions with Answer Keys | SAT Online Course AMBiPi.
SAT 2022 Practice Questions Test 15 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
A company sponsors a health program for its employees by partnering with a local gym. If employees pay for a yearlong membership at this gym, then for every day the employee uses his or her swipe card to enter the gym (and work out), the company reimburses the employee 0.2% of the cost of the $220 membership. Additionally, any employee who goes to the gym more than 60% of the days in the year gets one bonus paid day off of work. The company uses a 365-day year.
If 246 employees participate in the program and they each go to the gym an average of 84 days per year, how much money in membership reimbursements will the company payout? Round your answer to the nearest whole dollar.
Show/Hide Answer Key
Correct Answer: 9092
Difficulty: Medium
Category: Problem Solving and Data Analysis / Rates, Ratios, Proportions, and Percentages
Strategic Advice: Break this problem into short steps to keep all of the information organized.
Getting to the Answer: Step one: Determine how many days total the company needs to make reimbursements for by multiplying the number of employees by the average number of days they each go to the gym: 246 × 84 = 20,664.
Step two: Determine the amount of money the company must reimburse per day by multiplying the daily reimbursement rate, 0.2% by the cost of the membership: $220 × 0.002 = $0.44.
Step three: Find the total amount the company must pay in reimbursements by multiplying the total number of days for which it must make reimbursements by the amount it must pay per day: 20,664 × $0.44 = $9,092.16 = $9,092.
SAT Math Practice Online Test Question No 2:
Rory left home and drove straight to the airport at an average speed of 45 miles per hour. He returned home along the same route, but traffic slowed him down and he only averaged 30 miles per hour on the return trip. If his total travel time was 2 hours and 30 minutes, how far is it, in miles, from Rory’s house to the airport?
Show/Hide Answer Key
Correct Answer: 45
Difficulty: Hard
Category: Problem Solving and Data Analysis / Rates, Ratios, Proportions, and Percentages
Strategic Advice: Make a chart that represents rate, time, and distance and fill in what you know. Then use your table to solve for distance. If it took Rory t hours to get to the airport, and the total trip took 2 hours and 30 minutes (or 2.5 hours), how long (in terms of t) did the return trip take?
Getting to the Answer:
Now use the formula d = r × t for both parts of the trip: d = 45t and d = 30(2.5 – t). Because both are equal to d, you can set them equal to each other and solve for t:
45t = 30(2.5 – t)
45t = 75 – 30t
75t = 75
t = 1
Now plug back in to solve for d:
d = 45t
d = 45(1)
d = 45
SAT Math Practice Online Test Question No 3:
(4h – (21 – 8h)/3 = 15 + 6(h – 1)/2
What is the value of h in the equation above?
Show/Hide Answer Key
Correct Answer: 11.5 or 23/2 or 69/6
Difficulty: Easy
Category: Heart of Algebra / Linear Equations
Strategic Advice: Simplify the numerators, then cross-multiply and solve using inverse operations.
Getting to the Answer: Simplify each numerator. Then, cross-multiply. Finally, isolate the variable using inverse operations.
[4h – (21 – 8h)]/3 = [15 + 6(h – 1)]/2
(4h – 21 + 8h)/3 = (15 + 6h – 6)/2
(12h – 21/)3 = (6h + 9)/2
2(12h – 21) = 3(6h + 9)
24h – 42 = 18h + 27
6h = 69
h = 69/6 = 23/2 = 11.5
SAT Math Practice Online Test Question No 4:
The volume of a rectangular shipping crate being loaded onto a barge for international shipment across the Panama Canal is 10,290 cubic feet. If the length to width to height ratio of the crate is 3:5:2 (in that order), what is the length of the crate in feet?
Show/Hide Answer Key
Correct Answer: 21
Difficulty: Medium
Category: Additional Topics in Math / Geometry
Strategic Advice: Use the formula for finding the volume of a rectangular solid, V = lwh, to write an equation. Because the dimensions are given as the ratio 3:5:2, let the length, width, and height be represented by 3x, 5x, and 2x.
Getting to the Answer: Substitute the expressions into the formula and solve for x.
10,290 = (3x)(5x)(2x)
10,290 = 30x3
343 = x3
7 = x
The length was represented by 3x, so multiply to find that the length is 3(7) = 21 feet.
SAT Math Practice Online Test Question No 5:
Three cars all arrive at the same destination at 4:00 PM. The first car traveled 144 miles mostly by highway. The second car traveled 85 miles mainly on rural two-lane roads. The third car traveled 25 miles primarily on busy city streets.
The first car traveled at an average speed of 64 mph. The second car started its drive at 2:18 PM. How many minutes had the first car already been traveling before the second car started its drive?
Show/Hide Answer Key
Correct Answer: 33
Difficulty: Medium
Category: Problem Solving and Data Analysis / Rates, Ratios, Proportions, and Percentages
Strategic Advice: Questions that involve distance, rate, and time can almost always be solved using the formula Distance = rate × time.
Getting to the Answer: Use the speed, or rate, of the first car (64 mph) and its distance from the destination (144 mi) to determine how long it traveled. You don’t know the time, so call it t.
Distance = rate x time
144 = 64t
2.25 = t
This means it took 2.25 hours for the first car to arrive. You need the number of minutes, so multiply 2.25 by 60 to get 60 × 2.25 = 135 minutes. Now determine how long it took the second car. It started its drive at 2:18 PM and arrived at 4:00 PM, so it took 1 hour and 42 minutes, or 102 minutes. This means that the first car had been traveling for 135 – 102 = 33 minutes before the second car started its drive.
SAT Math Practice Online Test Question No 6:
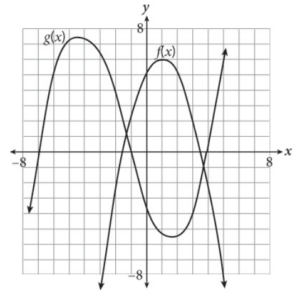
The graph above shows a quadratic function f(x) and a cubic function g(x). Based on the graph, what is the value of (f – g)(3), assuming all integer values?
Show/Hide Answer Key
Correct Answer: 6
Difficulty: Medium
Category: Passport to Advanced Math / Functions
Strategic Advice: Understanding the language of functions will come in very handy on Test Day. Here, (f – g)(3) means f(3) – g(3). You don’t know the equations of the functions, so you’ll need to read the values from the graph.
Getting to the Answer: Graphically, f(3) means the y-value at x = 3 on the graph of f, which is 2. Likewise, g(3) means the y-value at x = 3 on the graph of g, which is –4. The difference, f – g, is 2 – (–4) = 6.
SAT Math Practice Online Test Question No 7:
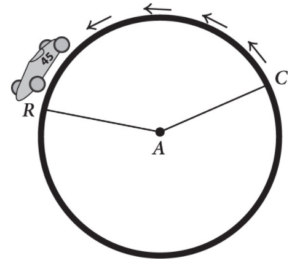
Most racetracks are in the shape of an ellipse (an elongated circle similar to an oval), but Langhorne Speedway in Pennsylvania was originally a circular track. If a racecar is traveling around this track, starting at point C and traveling 1,500 feet to point R, and the radius of the track is 840 feet, what is the measure to the nearest degree of minor angle CAR?
Show/Hide Answer Key
Correct Answer: 102
Difficulty: Medium
Category: Additional Topics in Math / Geometry
Strategic Advice: The distance around part of a circle is the same as arc length, so use the relationship
arc length/circumference = central angle/ 360° to answer the question.
Getting to the Answer: The unknown in the relationship is the central angle, so call it A. Before you can fill in the rest of the equation, you need to find the circumference of the circle: C = 2πr = 2π(840) = 1,680π.
Now you’re ready to solve for A: arc length/circumference = central angle/360°
1,500/1,680π = A/360
1,500 x 360/1,680π = A
102.314 ≈ A
Be careful when you enter this expression into your calculator—you need to put 1,680π in parentheses so that the calculator doesn’t divide by 1,680 and then multiply by π. If entered correctly, the result is about 102 degrees.
SAT Math Practice Online Test Question No 8:
The Great Depression began in 1929 and lasted until 1939. It was a period of extreme poverty, marked by low prices and high unemployment. The main catalytic event to the Great Depression was the Wall Street Crash (stock market crash). The Dow, which measures the health of the stock market, started Black Thursday (October 24, 1929) at approximately 306 points.
By the end of business on Black Thursday, the Dow had dropped by 2%. Over the course of Friday and the half-day Saturday session, there was no significant change. Unfortunately, the market lost 13% on Black Monday, followed by another 12% on Black Tuesday. What was the total percent decrease from opening on Black Thursday to closing on Black Tuesday? Round your answer to the nearest whole percent and ignore the percent sign when entering your answer
Show/Hide Answer Key
Correct Answer: 25
Difficulty: Hard
Category: Problem Solving and Data Analysis / Rates, Ratios, Proportions, and Percents
Strategic Advice: Percent change is given by the ratio amount of change/original amount, To find the total percent change, you’ll need to work your way through each of the days, and then use the ratio. Jot down the Dow value at the end of each day as you go. Do not round until you reach your final answer.
Getting to the Answer: First, calculate the value of the Dow at closing on Black Thursday: It opened at 306 and decreased by 2%, which means the value at the end of the day was 100 – 2 = 98% of the starting amount, or 306 × 0.98 = 299.88. Then, it decreased again on Monday by 13% to close at 100 – 13 = 87% of the opening amount, or 299.88 × 0.87 = 260.8956. Finally, it decreased on Tuesday by another 12% to end at 100 – 12 = 88% of the starting amount, or 260.8956 × 0.88 = 229.588. Now use the percent change formula to calculate the percent decrease from opening on Black Thursday (306) to closing on Black Tuesday (229.588): Percent decrease = 306 – 229.588/306 = 76.412/306 = 0.2497
The Dow had a total percent decrease of approximately 25% between opening on Black Thursday and closing on Black Tuesday.
SAT Math Practice Online Test Question No 9:
Heating water accounts for a good portion of the average home’s energy consumption. Tankless water heaters, which run on natural gas, are about 22% more energy efficient on average than electric hot water heaters. However, a tankless hot water heater typically costs significantly more. Suppose one tankless water heater costs $160 more than twice as much as a conventional hot water heater. If both water heaters cost $1,000 together, how many more dollars does the tankless water heater cost than the conventional one?
Show/Hide Answer Key
Correct Answer: 440
Difficulty: Medium
Category: Heart of Algebra / Systems of Linear Equations
Strategic Advice: Translate from English into math to write a system of equations with t = the cost of the tankless heater in dollars, and c = the cost of the conventional heater in dollars.
Getting to the Answer: First, a tankless heater (t) costs $160 more (+160) than twice as much (2c) as the conventional one, or t = 2c + 160. Together, a tankless heater (t) and a conventional heater (c) cost $1,000, or t + c = 1,000.
The system is: {t = 2c + 160, t + c = 1,000}
The top equation is already solved for t, so substitute 2c + 160 into the second equation for t and solve for c:
2c + 160 + c = 1,000
3c + 160 = 1,000
3c = 840
c = 280
Be careful—that’s not the answer! The conventional hot water heater costs $280, so the tankless heater costs 2(280) + 160 = $720. This means the tankless heater costs $720 – $280 = $440 more than the conventional heater.
SAT Math Practice Online Test Question No 10:
After a surface has been cleaned, bacteria begin to regrow. Because bacteria reproduce in all directions, the area covered is usually in the shape of a circle. The diameter of the circle in millimeters can give scientists an idea of how long the bacteria have been growing. For a certain kind of bacteria, the equation d = 0.015 x √h – √24, can be used to find the number of hours, h ≥ 24, that the bacteria have been growing. If the diameter of a circle of these bacteria is 0.12 millimeters, how many hours have the bacteria been growing?
Show/Hide Answer Key
Correct Answer: 88
Difficulty: Hard
Category: Passport to Advanced Math / Exponents
Strategic Advice: When you’re asked to solve an equation that has two variables, the question usually gives you the value of one of the variables. Read carefully to see which variable is given and which one you’re solving for.
Strategic Advice: When you’re asked to solve an equation that has two variables, the question usually gives you the value of one of the variables. Read carefully to see which variable is given and which one you’re solving for.
0.12 = 0.015 x √h – √24
8 = √h – √24
82 = (√h – √24)2
64 = h – 24
88 = h