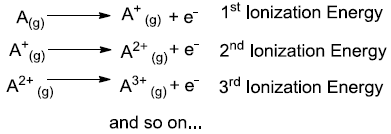NSEJS PREVIOUS PAPERS 2015-2016
In this post, you will get NSEJS Previous Papers 2015-2016. NSEJS is the first phase of IJSO, it is organized by the IAPT with HBCSE. The full form of NSEJS is National Standard Examination in Junior Science.
| NSEJS | |||||||
|---|---|---|---|---|---|---|---|
| Previous Year Question Papers | |||||||
| 2008-09 | 2009-10 | 2010-11 | 2011-12 | 2012-13 | |||
| 2013-14 | 2014-15 | 2015-16 | 2016-17 | 2017-18 | |||
| 2018-19 | 2019-20 | ||||||
PART A : Only ONE out of four options is correct
Read More : 129 Maths Short Tricks
NSEJS Previous Papers 2015-2016 Ques No 1:
Which of the following graphs is correct for a particle moving in a circle of radius r at a speed of v (where ‘a’ is magnitude of acceleration) ?
Options:
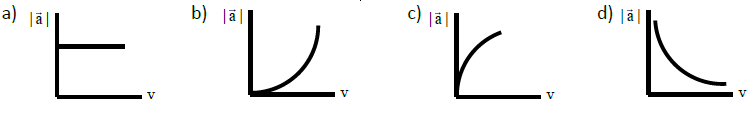
NSEJS Previous Papers 2015-2016 Ques No 2:
Electronic configuration of Na+ is (2,8) and that of sodium element is (2,8,1). Choose the correct statements.
(i) Na+(g) is more stable than Na(g).
(ii) Na+(g) is less stable than Na(g).
(iii) Na+(aq) is more stable than Na(aq).
(iv) Na+(aq) is less stable than Na(aq).
Options:
A. ii, iii
B. i, iii
C. ii, iv
D. i, iv
NSEJS Maths Questions Bank EBook
Get NSEJS 2008 to 2018 Maths Questions Bank with Solutions. To get this combo ebook, click below RED button.
NSEJS Previous Papers 2015-2016 Ques No 3:
What will be the remainder if the number 72015 is divided by 25?
Options:
A. 1
B. 7
C. 18
D. 24
NSEJS Previous Papers 2015-2016 Ques No 4:
In humans, the digestion of carbohydrates happens/takes place in the following parts of the digestive system:
Options:
A. Mouth, stomach and small intestine
B. Mouth and small intestine
C. Small intestine alone
D. Stomach and small intestine
NSEJS Previous Papers 2015-2016 Ques No 5:
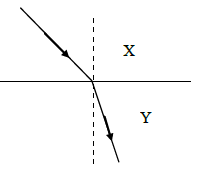
Light travels from medium X to medium Y as shown in the adjacent figure
Options:
A. both the speed and frequency decrease
B. speed increases and frequency decreases
C. the speed decreases and wavelength decrease
D. the speed decreases and wavelength increases
NSEJS Previous Papers 2015-2016 Ques No 6:
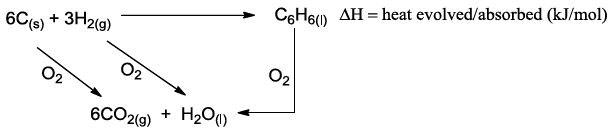
Hess’ Law states that ‘the heat evolved or absorbed in a chemical reaction is the same whether the process takes place in one or in several steps
Heat evolved in the combustion of one mole C(s) in excess oxygen is x kJ/mol, and that for the
combustion of H2(g) is y kJ/mol and for that of C6H6 (l) is z kJ/mol. Therefore, the heat change
(kJ/mol) involved in the formation one mole of C6H6 (l) from the given equation is
Options:
A. x+y+z
B. 6x+3y-z
C. 6x+3y+z
D. x+y-z/6
NSEJS Previous Papers 2015-2016 Ques No 7:
If A(p, q + r), B(q, r + p) and C(r, p + q) are points then area of triangle ABC
Options:
A. p2 + q2 + r2
B. (p + q + r)2
C. 6x+3y+z
D. zero
NSEJS Previous Papers 2015-2016 Ques No 8:
Photosynthesis in plants is carried out in
Options:
A. leaves
B. leaves and stems
C. leaves, stems and aerial roots
D. stems and roots
NSEJS Previous Papers 2015-2016 Ques No 9:
A particle moves along the x-axis according to the equation x = 6t2 where x is displacement
in meters and t is time in seconds. Therefore
Options:
A. the acceleration of the particle is 6 ms-2
B. the particle follows a parabolic path
C. each second the velocity of the particle changes by 9.8 ms-1
D. the velocity of the particle is 6 ms-1 at t = 0.5 s
NSEJS Previous Papers 2015-2016 Ques No 10:
What occurs when H2O(l) evaporates
(i) Covalent bonds are broken.
(ii) Only dipole-dipole forces are overcome
(iii) Heat is absorbed by water from the surroundings
(iv) It becomes oxygen and hydrogen gas
Options:
A. Only (i) and (iii) occurs
B. Only (ii) and (iii) occurs
C. (i), (iii) and (iv) occurs
D. (i), (ii), (iii) and (iv) take place
NSEJS Previous Papers 2015-2016 Ques No 11:
3/4 + 3/28 + 3/70 + 3/130 + … + 3/9700 = ?
Options:
A. 0.97
B. 0.99
C. 1
D. 1.03
NSEJS Previous Papers 2015-2016 Ques No 12:
The following technique that can be used for deciphering the arrangement of nucleotide in
genes.
Options:
A. karyotyping
B. nucleic acid sequencing
C. DNA finger printing
D. transcription
NSEJS Previous Papers 2015-2016 Ques No 13:
The “reaction” force does not cancel the “action” force because
Options:
A. the action force is greater than the reaction force
B. the reaction force exists only after the action force is removed
C. the reaction force is greater than the action force
D. they act on different bodies
NSEJS Previous Papers 2015-2016 Ques No 14:
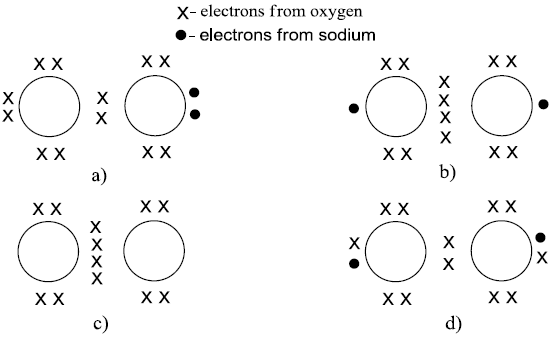
Which of the following Lewis dot structures best describes the structure of peroxide ion of sodium peroxide?
Options:
NSEJS Previous Papers 2015-2016 Ques No 15:
What is the sum of all three digit even numbers divisible by seventeen?
Options:
A. 18846
B. 18684
C. 14688
D. 16848
NSEJS Previous Papers 2015-2016 Ques No 16:
When a red blood cell was placed in an animal cell (RBC) in 3 different solutions, the following morphological observations were made under a microscope.
The above three solutions can be classified in the order of
Options:
A. isotonic, hypotonic and hypertonic
B. hypotonic, isotonic and hypertonic
C. hypotonic, hypertonic and isotonic
D. isotonic, hypertonic and hypotonic
NSEJS Previous Papers 2015-2016 Ques No 17:
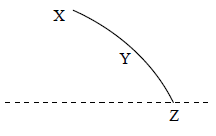
A stone is thrown horizontally and follows the XYZ path as shown in the adjacent figure. The direction of the acceleration of the stone at point Y is.
Options:
A. ↓
B. →
C. ↘
D. ↙
NSEJS Previous Papers 2015-2016 Ques No 18:
Ionization Energy is defined as ‘the energy required for removing the most loosely bound electron from an isolated gaseous atom or ion’. Identify element A.
Options:
A. Nitrogen
B. Oxygen
C. Carbon
D. Fluorine
NSEJS Previous Paper 2015-2016 Ques No 19:
The adjacent sides of a parallelogram are 30 cm and 20 cm. The length of one of the diagonal is 40 cm. What is the length of the other diagonal?
Options:
A. 60 cm
B. 10sqrt(10) cm
C. 20sqrt(5) cm
D. 8sqrt(30) cm
NSEJS Previous Paper 2015-2016 Ques No 20:
Genetic material (DNA) in plants occurs in which of the following cell organelles?
Options:
A. Nucleus
B. Nucleus and chloroplast
C. Nucleus, chloroplast and mitochondria
D. Chloroplast and mitochondria
NSEJS Previous Paper 2015-2016 Ques No 21:
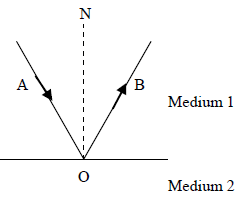
The diagram shows total internal reflection. Which of the following statement is not true?
Options:
A. Angle AON is the incident angle
B. angle AON = angle BON
C. angle AON is the critical angle
D. the speed of light in medium 2 is greater than that in medium 1
NSEJS Previous Paper 2015-2016 Ques No 22:
A chemist’s report on a batch of pharmaceutical products, Aspirin (C9H8O4) (250mg tablets) and Paracetamol (C8H9NO2) (500mg tablets) indicated a ‘+0.5%’ weight error in each tablet. Due to this error, the consumer gets extra ‘x’ molecules of aspirin per tablet and extra ‘y’ molecules of paracetamol per tablet. Choose the ‘best’ relation between x and y.
Options:
A. x = y
B. x > y
C. x < y
D. x = 2y
For full paper of NSEJS Previous Paper 2015-2016, Click Here
For solution of NSEJS Previous Paper 2015-2016, Click Here
| NSEJS | |||||||
|---|---|---|---|---|---|---|---|
| Previous Year Question Papers | |||||||
| 2008-09 | 2009-10 | 2010-11 | 2011-12 | 2012-13 | |||
| 2013-14 | 2014-15 | 2015-16 | 2016-17 | 2017-18 | |||
| 2018-19 | 2019-20 | ||||||
NSEJS Maths Questions Bank EBook
Get NSEJS 2008 to 2018 Maths Questions Bank with Solutions. To get this combo ebook, click below RED button.