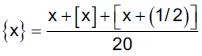Pre RMO 2019 Question Paper with Answer Keys

Pre RMO 2019 is the first stage exam for Math Olympiad Exams. It was scheduled on 25 August 2019 at 10 AM to 1 PM.

Read: Get More Details About Pre RMO

Pre RMO 2019 Question Paper (25 August)

Pre RMO 2019 conducted on 25 August 2019.

Pre RMO 2019 Answer Keys (25 August)

Read: Pre RMO and RMO Important Study Materials: Books | PDFs | Blogs | YouTube Channels | Solved Papers

Pre RMO 2019
Answer Keys (25 August)
Ques No	Ans Key	Ques No	Ans Key	Ques No	Ans Key	Ques No	Ans Key
1	04	9	14	17	30	25	48
2	13	10	55	18	20	26	50
3	13	11	06	19	13	27	84
4	36	12	18	20	Bonus	28	15
5	10	13	10	21	17	29	47
6	29	14	53	22	78	30	64
7	51	15	45	23	55
8	49	16	40	24	37

Pre RMO 25 August 2019 Solutions

Pre RMO 25 August 2019 Question No 1

Consider the sequence of numbers

for n ≥ 1, where [x] denotes the greatest integer not exceeding x. If the missing integers in the sequence are n₁ < n₂ < n₃ < … , then find n₁₂.

Solution:

Pre RMO 25 August 2019 Question No 2

If x = √2 + √3 + √6 is a root of the x⁴ + ax³ + bx² + cx + d where a, b, c, d are integers, what is the value of |a + b + c + d|?

Solution:

Pre RMO 25 August 2019 Question No 3

Find the number of positive integers less than 101 that cannot be written as the difference of two squares of integers.

Solution:

Pre RMO 25 August 2019 Question No 4

Let a₁ = 24 and form the sequence an, n ≥ 2 by a_n = 100a_n-1 + 134. The first few terms are 24, 2534, 253534, 25353534, … . What is the least value of n for which a_n is divisible by 99?

Solution:

Pre RMO 25 August 2019 Question No 5

Let N be the smallest positive integer such that N + 2N + 3N + … + 9N is a number all whose digits are equal. What is the sum of the digits of N?

Solution:

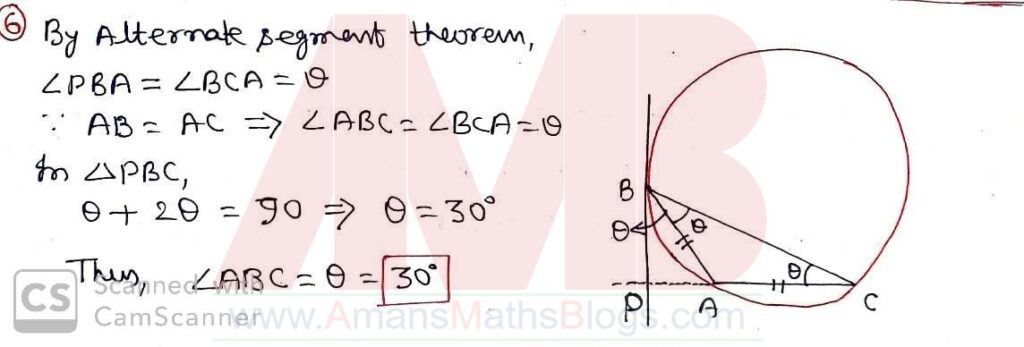
Pre RMO 25 August 2019 Question No 6

Let ABC be a triangle such that AB = AC. Suppose the tangent to the circumcircle of triangle ABC at B is perpendicular to AC. Find the angle ABC measured in degree.

Solution:

Pre RMO 25 August 2019 Question No 7

Let s(n) denote the sum of the digits of a positive integer n in base 10. If s(m) = 20 and s(33m) = 120, what is the value of s(3m)?

Solution:

Pre RMO 25 August 2019 Question No 8

Let F_k(a, b) = (a + b)^k – a^k – b^k and let S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. For how many ordered pairs (a, b) with a, b ∈ S and a ≤ b is F₅(a, b) / F₃(a, b) an integer?

Solution:

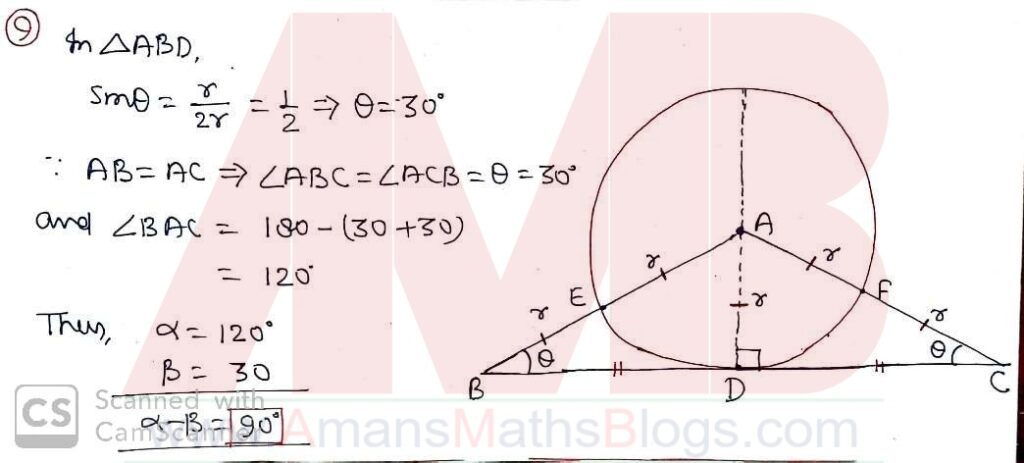
Pre RMO 25 August 2019 Question No 9

The centre of the circle passing through the midpoints of the sides of an isosceles triangle ABC lies on the circumcircle of triangle ABC. If the larger angle of triangle ABC is α^o and the smaller one β^o then what is the value of (α – β)?

Solution:

Pre RMO 25 August 2019 Question No 10

One day I went for a walk in the morning at x minutes past 5’O clock, where x is a two digit number. When I returned, it was y minutes past 6’O clock, and I noticed that (i) I walked exactly for x minutes and (ii) y was a 2 digit number obtained by reversing the digits of x. How many minutes did I walk?

Solution:

Pre RMO 25 August 2019 Question No 11

Find the largest value of ab such that the positive integers a, b > 1 satisfy a^bb^a + a^b +b^a = 5329.

Solution:

Pre RMO 25 August 2019 Question No 12

Let N be the number of ways of choosing a subset of 5 distinct numbers from the set {10a + b: 1 ≤ a ≤ 5, 1 ≤ b ≤ 5} where a, b are integers, such that no two of the selected numbers have the same units digit and no two have the same tens digit. What is the remainder when N is divided by 73?

Solution:

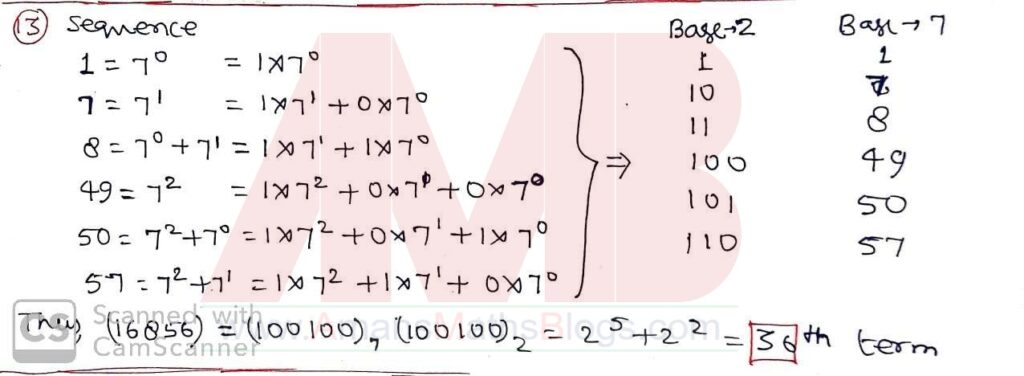
Pre RMO 25 August 2019 Question No 13

Consider the sequence 1, 7, 8, 49, 50, 56, 57, 343, … which consists of sums of distinct powers of 7, that is, 7⁰, 7¹, 7⁰ + 7¹, 7², … in increasing order. At what position will 16856 occur in this sequence?

Solution:

Pre RMO 25 August 2019 Question No 14

Let R denote the circular region in the xy-plane bounded by the circle x² + y² = 36. The lines x = 4 and y = 3 divide R into four regions R_i, i = 1, 2, 3, 4. If |R_i| denotes the area of the region R_i and if |R₁| > |R₂| > |R₃| > |R₄|, determines |R₁| – |R₂| – |R₃| + |R₄|. (here |A| denotes the area of the region A in the plane.)

Solution:

Pre RMO 25 August 2019 Question No 15

In base – 2 notation, digits are 0 and 1 only and the places go up in powers of – 2. For example, 11011 stands for (-2)⁴ + (-2)³ + (-2)¹ + (-2)⁰ and equals number 7 in base 10. If the decimal number 2019 is expressed in the base – 2 how many non zero digits does it contain?

Solution:

Pre RMO 25 August 2019 Question No 16

Let N denote the number of all natural numbers n such that n is divisible by a prime p > √n and p < 20. What is the value of N?

Solution:

Pre RMO 25 August 2019 Question No 17

Let a, b, c be distinct positive integers such that b + c – a, c + a – b and a + b – c are all perfect squares. What is the largest possible value of a + b + c smaller than 100?

Solution:

Pre RMO 25 August 2019 Question No 18

What is the smallest prime number p such that p³ + 4p² + 4p has exactly 30 positive divisors?

Solution:

Pre RMO 25 August 2019 Question No 19

If 15 and 9 are lengths of two medians of a triangle, what is the maximum possible area of the triangle to the nearest integer?

Solution:

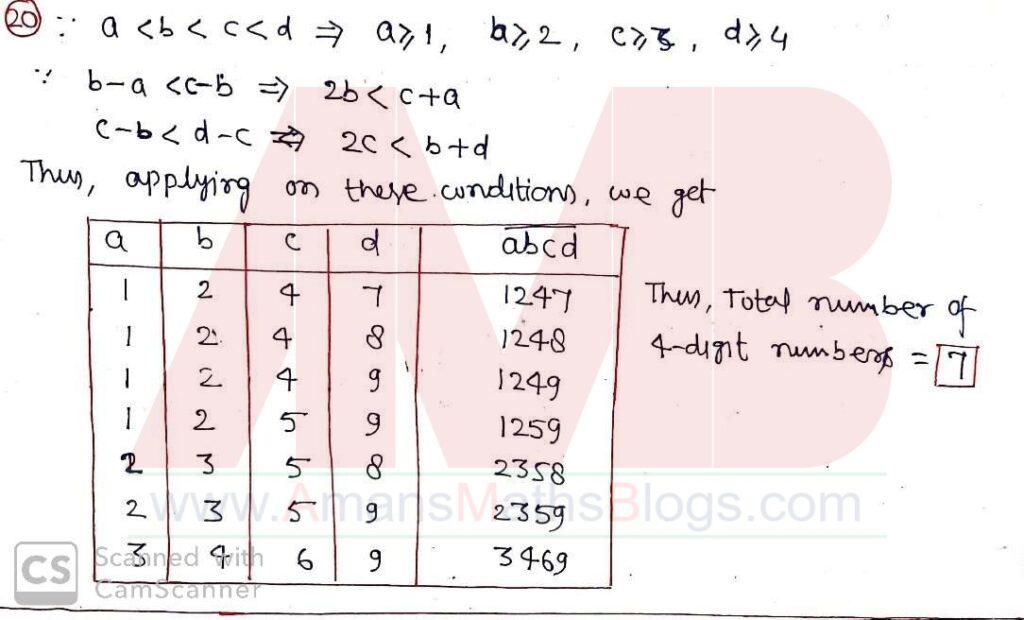
Pre RMO 25 August 2019 Question No 20

How many 4-digit numbers abcd are there such that a < b < c < d and b – a < c – b < d – c?

Solution:

Pre RMO 25 August 2019 Question No 21

Consider the set E of all positive integers n such that when divided by 9, 10, 11 respectively, the remainders (in that order) are all > 1 and form a non-constant geometric progression. If N is the largest element of E, find the sum of digits of E. 

Solution: BONUS because E is set of positive integers. We cannot find the sum of its digits of E.

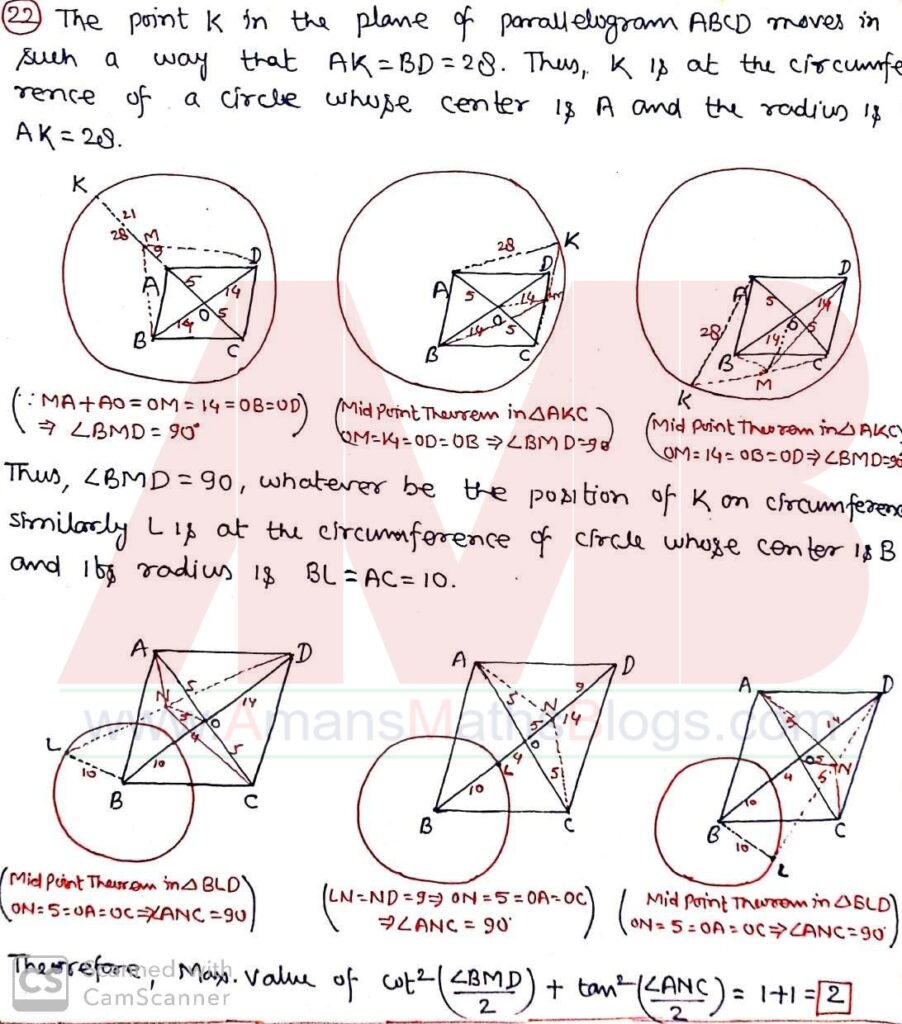
Pre RMO 25 August 2019 Question No 22

In parallelogram ABCD, AC = 10 and BD = 28. The points K and L in the plane of ABCD move in such a way that AK = BD and BL = AC. Let M and N be the midpoints of CK and DL, respectively. What is the maximum value of cot²(∠BMD/2) + tan²(∠ANC/2) ?

Solution:

Pre RMO 25 August 2019 Question No 23

Let t be the area of a regular pentagon with each side equal to 1. Let P(x) = 0 be the polynomial equation with least degree, having integer coefficients, satisfied by x= t and the gcd of all the coefficients equal to 1. If M is the sum of the absolute values of the coefficients of P(x). What is the integer closest to √M. (sin18^o = (√5 – 1)/2)

Solution: It should be BONUS, because the value of sin18 is wrong.

Pre RMO 25 August 2019 Question No 24

For n ≥ 1, let a_n be the number beginning with n 9’s followed by 744 ; e.g., a4 = 9999744. Define f(n) = max {m  N | 2^m divides a_n}, for n ≥ 1. Find f(1) + f(2) + f(3) +…. + f(10).

Solution:

Pre RMO 25 August 2019 Question No 25

Let ABC be an isosceles triangle with AB = BC. A trisector of ∠B meets AC at D. If AB, AC and BD are integers and AB – BD = 3, find AC

Solution:

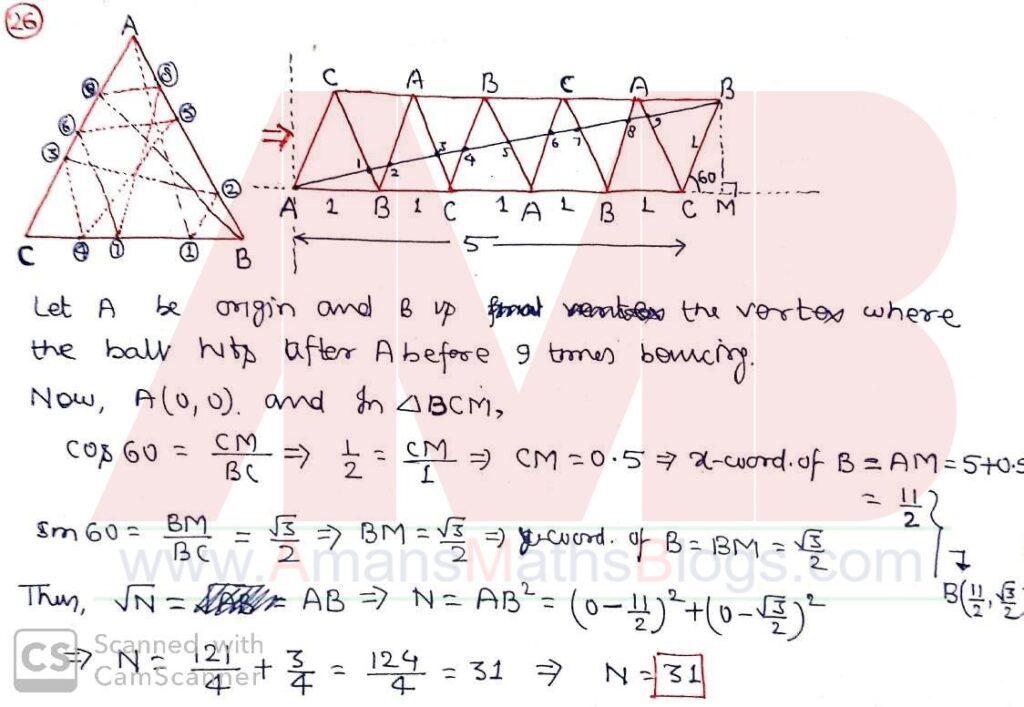
Pre RMO 25 August 2019 Question No 26

A friction-less board has the shape of an equilateral triangle of side length 1 meter with bouncing walls along the sides. A tiny super bouncy ball is fired from vertex A towards the side BC. The ball bounces off the walls of the board nine times before it hits a vertex for the first time. The bounces are such that the angle of incidence equal the angle of reflection. The distance traveled by the ball in meters is of the form √N , where N is an integer. What is the value of N ?

Solution:

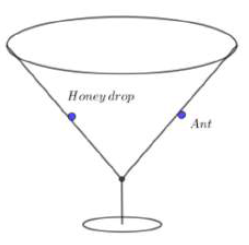
Pre RMO 25 August 2019 Question No 27

A conical glass is in the form of a right circular cone. The slant height is 21 and the radius of the top rim of the glass is 14. An ant at the mid point of a slant line on the outside wall of the glass sees a honey drop diametrically opposite to it on the inside wall of the glass. (see the figure ). If d the shortest distance it should crawl to reach the honey drop, what is the integer part of d ? (Ignore the thickness of the glass)

Solution:

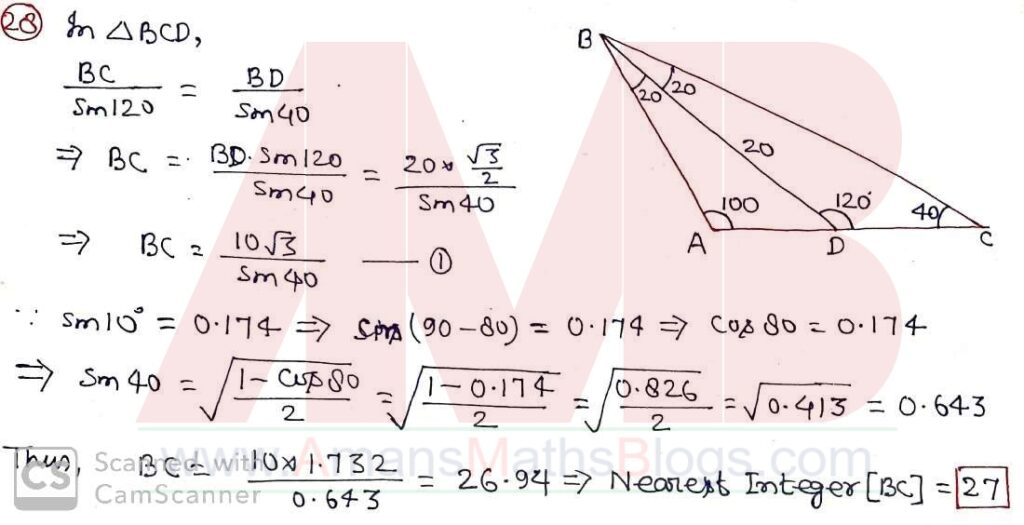
Pre RMO 25 August 2019 Question No 28

In a triangle ABC, it is known that ∠A = 100° and AB = AC. The internal angle bisector BD has length 20 units. Find the length of BC to the nearest integer, given that sin 10° ≅ 0.174.

Solution:

Pre RMO 25 August 2019 Question No 29

Let ABC be an acute angled triangle with AB =15 and BC = 8. Let D be a point on AB such that BD = BC. Consider points E on AC such that ∠DEB = ∠BEC. If α denotes the product of all possible value of AE, find [ α ] the integer part of α.

Solution: BONUS

Pre RMO 25 August 2019 Question No 30

For any real number x, let [x] denotes the integer part of x; {x} be the fractional part of x ({x} = x – |x|). Let A denote the set of all real numbers x satisfying

If S is the sum of all numbers in A, find [S]

Solution:

 

Answer KeyPaper AnalysisPaper Solutionpre rmo 2012 solutionspre rmo 2015 solutionspre rmo 2016 question paperpre rmo 2016 question paper pdfpre rmo 2016 solutionspre rmo 2017 question paperpre rmo 2017 question paper pdfpre rmo 2019 answer keyspre rmo 2019 question paperpre rmo 2019 solutionspre rmo 25 august 2019 question paper solutionspre rmo papers with solutions