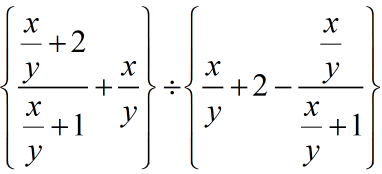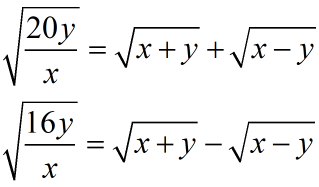Click Here To Get NMTC 2017 (5th & 6th) Answer Keys With Solution
Click Here To Get NMTC 2017 (7th & 8th) Answer Keys With Solution
NMTC 2017 (9th & 10th) Answer Keys With Solution
Part A: Instruction:
Only One of the choices A, B, C, D is correct. For each correct response, you get 1 mark. For each incorrect response, you lose 1/2 mark.
NMTC 2017 Paper For Junior Level Ques No 1:
If m is a real number such that m2 + 1 = 3m, the value of (2m5 – 5m4 + 2m3 – 8m2)/(m2 + 1) is
Options:
A. 1
B. 2
C. -1
D. -2
Solution:
NMTC Paper For Junior Level Ques No 2:
Consider the equation . The least positive a for which the solution x to the equation is a positive integer is
Options:
A. 1
B. 2
C. 3
D. 4
Solution:
NMTC Paper For Junior Level Ques No 3:
If x = 2017 and y = 1/2017, find the value of
Options:
A. 2017
B. 20172
C. 1/20172
D. 1
Solution:
NMTC Paper For Junior Level Ques No 4:
The ratio of an interior angle of a regular pentagon to an exterior angle of a regular decagon
Options:
A. 4 : 1
B. 3 : 1
C. 2 : 1
D. 7 : 3
Solution:
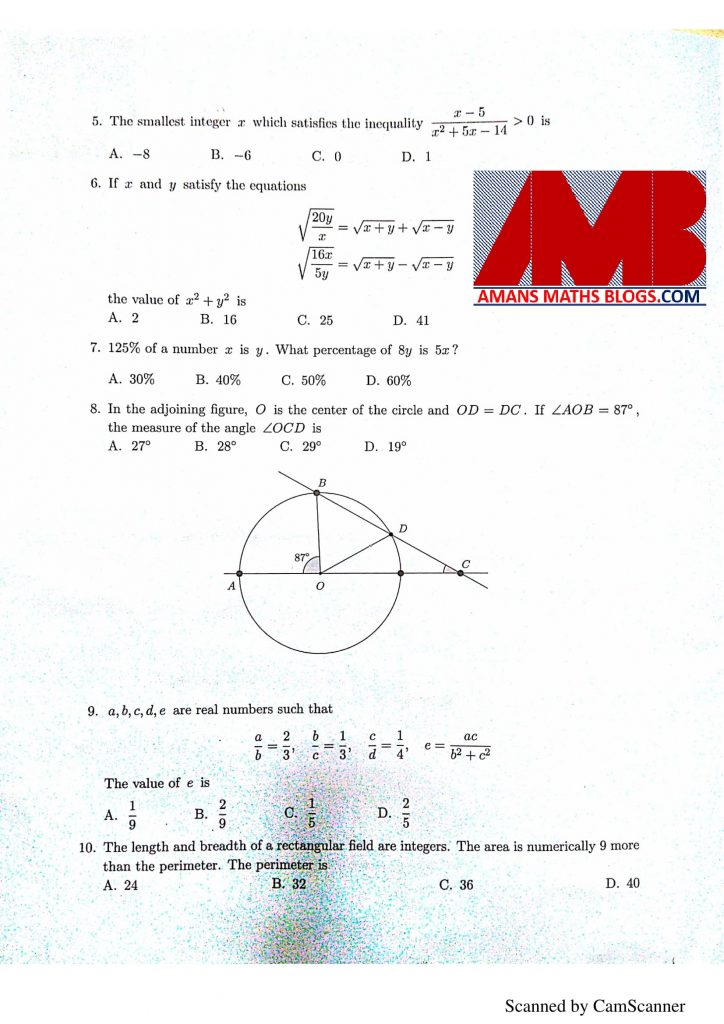
NMTC Paper For Junior Level Ques No 5:
The smallest integer x which satisfies the inequality (x – 5)/(x2 + 5x – 14) > 0 is
Options:
A. -8
B. -6
C. 0
D. 1
Solution:
NMTC Paper For Junior Level Ques No 6:
If x and y satisfy the equations
The value of x2 + y2 is
Options:
A. 2
B. 16
C. 25
D. 41
Solution:
NMTC 2017 Paper For Junior Level Ques No 7:
125% of a number x is y. What percentage of 8y is 5x?
Options:
A. 30%
B. 40%
C. 50%
D. 60%
Solution:
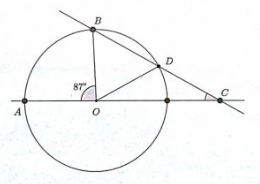
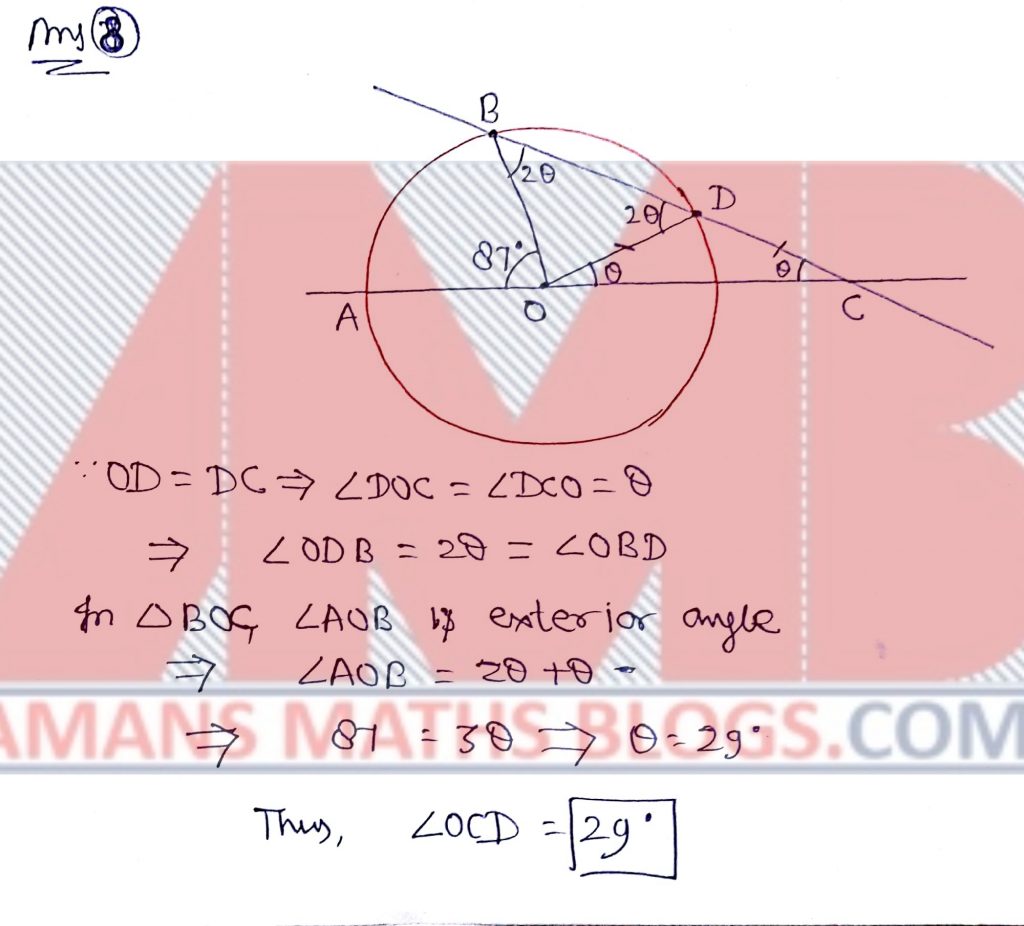
NMTC 2017 Paper For Junior Level Ques No 8:
In the adjoining figure, O is the center of the circle and OD = DC. If angle AOB = 87 degree, the measure of the angle OCD is
Options:
A. 27 degree
B. 28 degree
C. 29 degree
D. 19 degree
Solution:
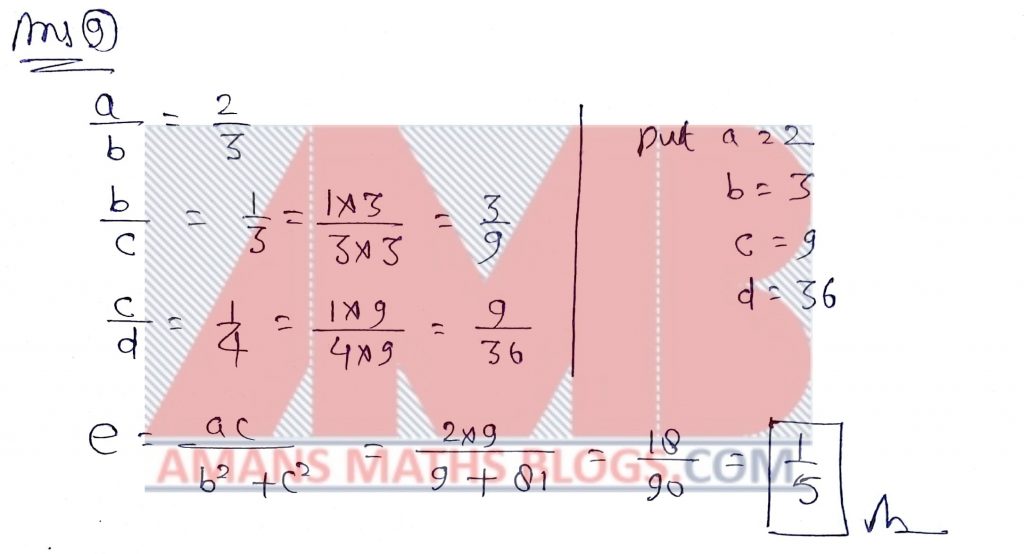
NMTC 2017 Paper For Junior Level Ques No 9:
a, b, c, d, e are real numbers such that a/b = 2/3, b/c = 1/3, c/d = 1/4, e = (ac)/(b2 + c2). The value of e is
Options:
A. 1/9
B. 2/9
C. 1/5
D. 2/5
Solution:
NMTC 2017 Paper For Junior Level Ques No 10:
The length and breadth of a rectangular field are integers. The area is numerically 9 more than the perimeter. The perimeter is
Options:
A. 24
B. 32
C. 36
D. 40
Solution:
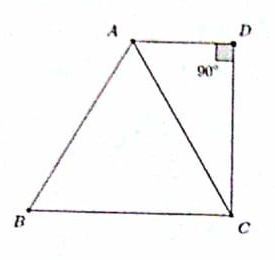
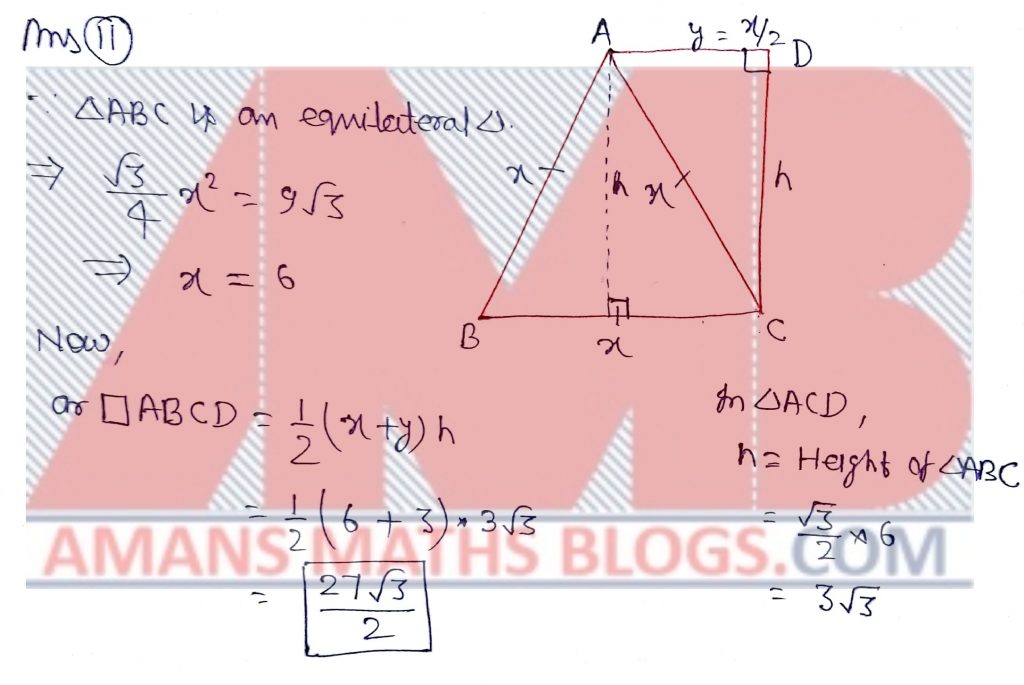
NMTC 2017 Paper For Junior Level Ques No 11:
ABCD is a trapezium in which ABC is an equilateral triangle with area 9 square units. If the angle ADC = 90 Degree, the area of the trapezium in square units is.
Options:
A. 12
B. 15/2
C. 27/2
D. 35/2
Solution:
NMTC 2017 Paper For Junior Level Ques No 12:
p is a prime number such that p2 – 8p – 65 > 0. The smallest value of p is
Options:
A. 7
B. 11
C. 13
D. 17
Solution:
NMTC 2017 Paper For Junior Level Ques No 13:
The least positive integer n such that 2015n + 2016n is divisible by 10 is
Options:
A. 1
B. 3
C. 4
D. None of these
Solution:
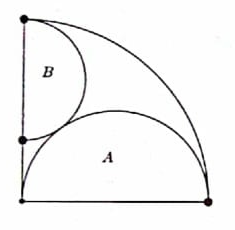
NMTC 2017 Paper For Junior Level Ques No 14:
In a quadrant of a circle of diameter 4 unit’s semicircle are drawn as shown. The radius of the smaller circle (B) is
Options:
A. 1/2
B. 1/3
C. 2/3
D. 3/4
Solution:
NMTC 2017 Paper For Junior Level Ques No 15:
The product of two positive integers is twice their sum; the product is also equal to six times the difference between the two integers. The sum of these integers is
Options:
A. 6
B. 7
C. 8
D. 9
Solution:
NMTC 2017 Paper For Junior Level Ques No 16:
n is a natural number such that n minus 12 is the square of an integer and n plus 19 is the square of another integer. The value of n is _____.
Solution:
NMTC 2017 Paper For Junior Level Ques No 17:
The number of there digit numbers which have odd number of factor is _____.
Solution:
NMTC 2017 Paper For Junior Level Ques No 18:
The positive integers a, b, c are connected by the inequality a2 + b2 + c2 + 3 < ab + 3b + 2c then the value of a + b + c is _____
Solution:
NMTC 2017 Paper For Junior Level Ques No 19:
The sum of all roots of the equation |3x – |1 – 2x|| = 2 is _____.
Solution:
NMTC 2017 Paper For Junior Level Ques No 20:
PQR is a triangle with PQ = 15, QR = 25, RP = 30. A,B are points on PQ and PR respectively such that PBA = PQR. The perimeter of the triangle PAB is 25, then the length of AB is_________.
Solution:
NMTC 2017 Paper For Junior Level Ques No 21:
A hare sees a bound 100 m away from her and runs off in the opposite at speed of 12 KM an hour. A minute later the bound perceive her and gives a chase at a speed of 16 KM an hour. The distance at which the bound catches the hare (in meters) is______.
Solution:
NMTC 2017 Paper For Junior Level Ques No 22:
Two circle touch both the arms of an angle whose measure is 60 Degree. Both the circle also touch each other externally. The radius of the smaller circle is r. The radius of the bigger circle (in terms of r) is______.
Solution:
NMTC 2017 Paper For Junior Level Ques No 23:
a, b are distinct natural numbers such that 1/a + 1/b = 2/5. If , the value of k is_______
Solution:
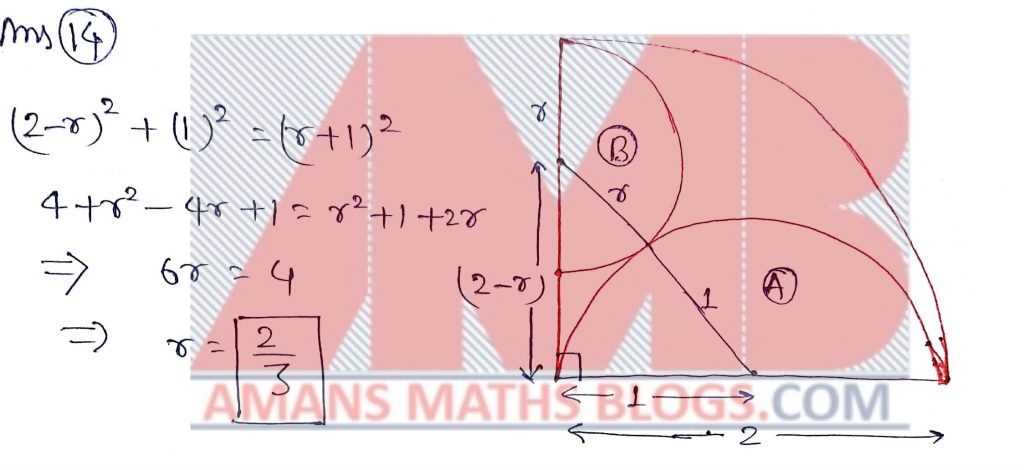
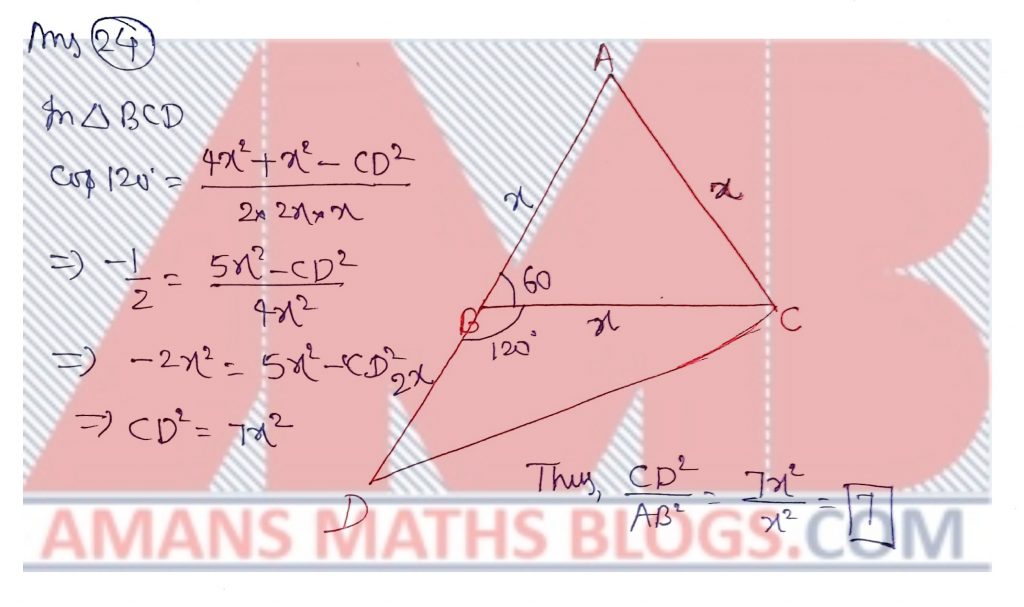
NMTC 2017 Paper For Junior Level Ques No 24:
The side AB of an equilateral triangle ABC is produced to D such that BD = 2AC. The value of CD2/AB2 is_____.
Solution:
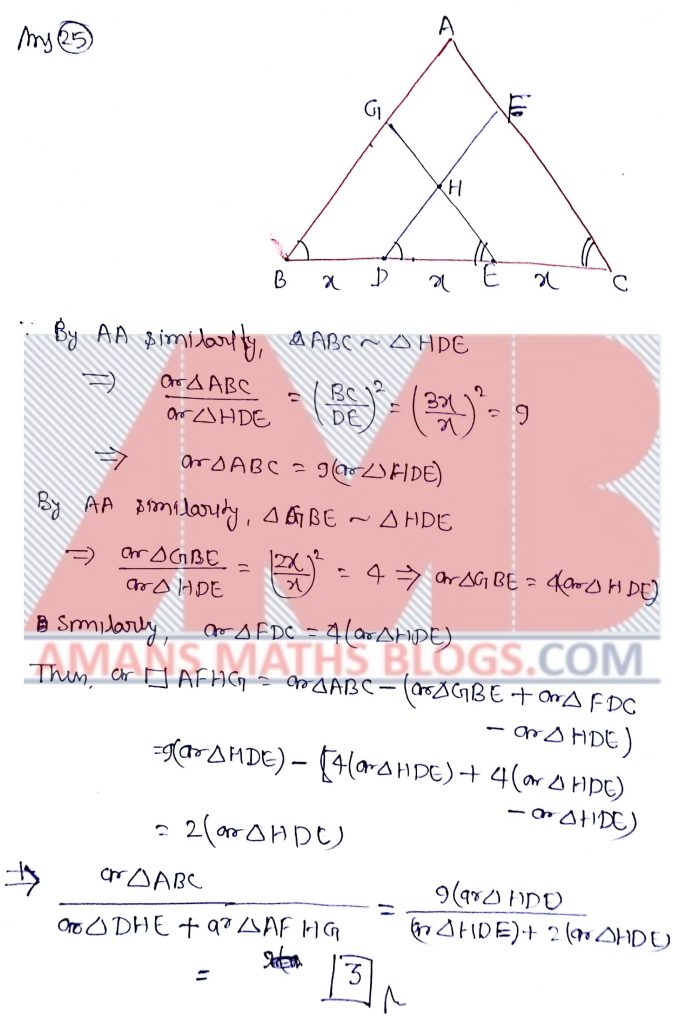
NMTC 2017 Paper For Junior Level Ques No 25:
D and E trisect the side BC of a triangle ABC. DF is drawn parallel to AB meeting AC at F. EG is drawn parallel to AC meeting AB at G. DF and EG cut at H. Then the numerical value of Area(ABC)/[Area (DHE) + Area (AFHG)] is_______.
Solution:
NMTC 2017 Paper For Junior Level Ques No 26:
In a examination 70% of the candidates passed in English, 65% passed in Mathematics, 27% failed in both the subjects and 248 passed in both the subjects. The total number of candidates is_____.
Solution:
NMTC 2017 Paper For Junior Level Ques No 27:
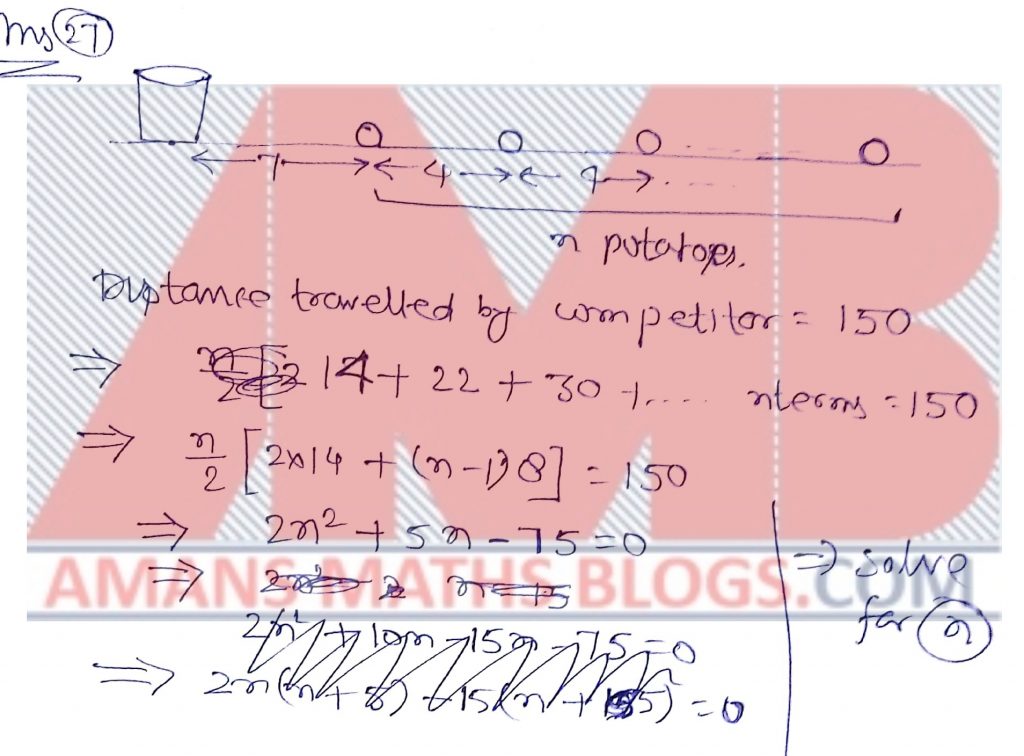
In a potato race, a bucket is placed at the starting point, which is 7 m from the first potato. The other potatoes are placed 4 m a part in a straight line from the first one. There are n potatoes in the line. Each competitor starts from the bucket, picks up the nearest potato, runs back with it, drops in the bucket, runs back to pick up the next potato up and dropped in the bucket. Each competitor ran a total of 150 m. The number of potatoes is_______.
Solution:
NMTC 2017 Paper For Junior Level Ques No 28:
A two-digit number is obtained by either multiplying the sum of its digits by 8 and adding 1, or by multiplying the difference of its digits by 13 and adding 2. The number is________.
Solution:
NMTC 2017 Paper For Junior Level Ques No 29:
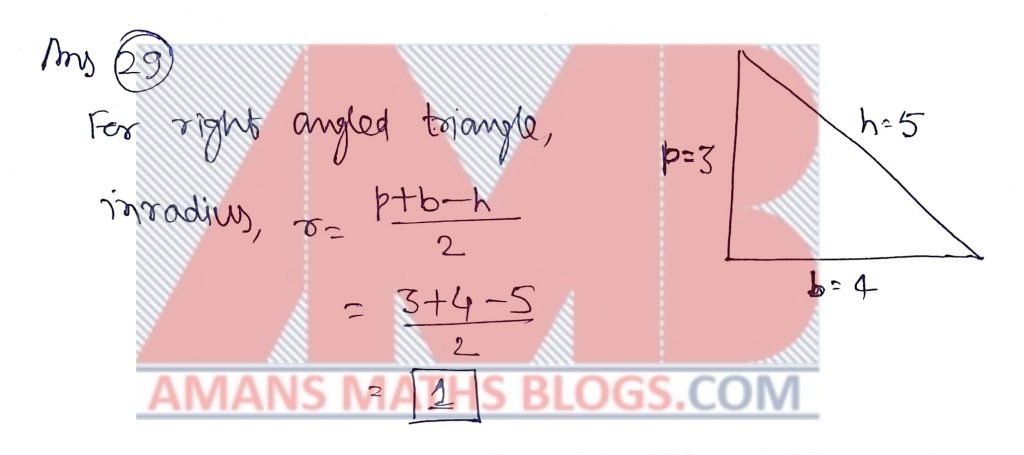
The inraduis of right angled triangle whose legs have lengths 3 and 4 is_____.
Solution:
NMTC 2017 Paper For Junior Level Ques No 30:
A, b are positive reals such that 1/a + 1/b = 1/(a + b). If (a/b)3 + (b/a)3 = 2 , where n is a natural number, the value of n is________.
Solution: