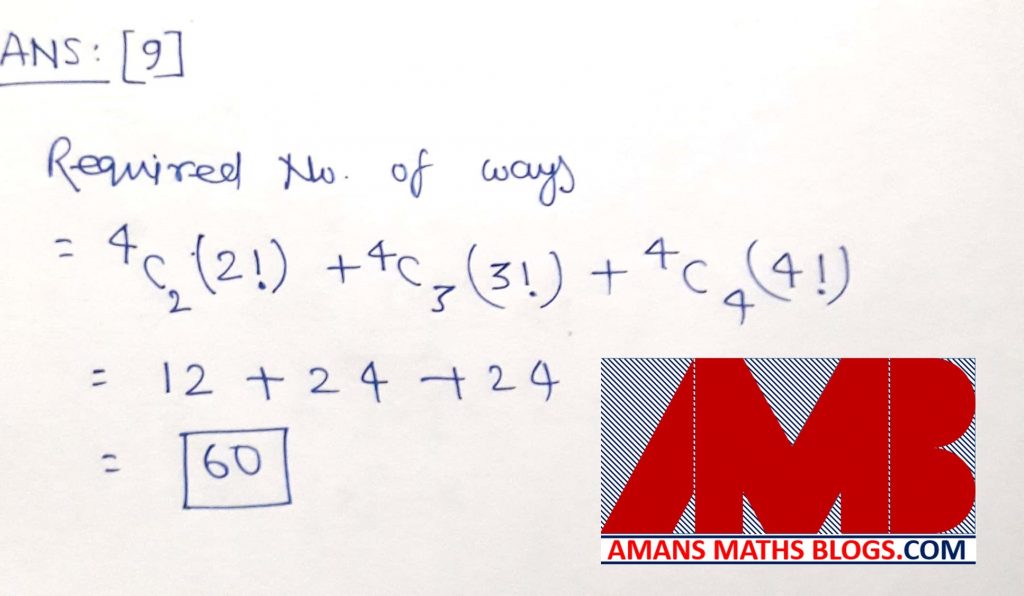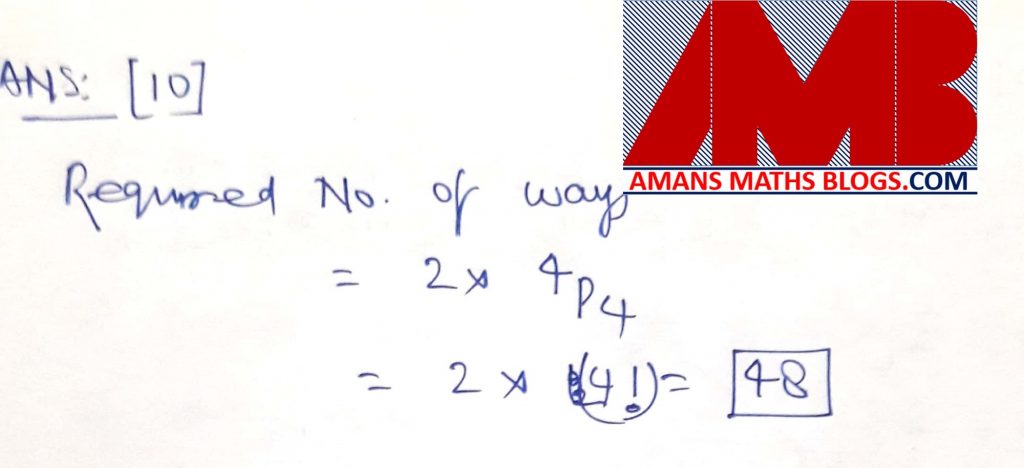Pre RMO 2017 Questions Paper with Answer Keys & Solution
What is Pre RMO 2017?
The Pre-Regional Mathematical Olympiad (PRMO of Pre RMO) is a national level examination cum scholarship programme. The scholarship programme is conducted by IAPT and students studying in class XI or below are eligible to appear for the PRMO 2017. PRMO was conducted in month of August across the nation.
Eligibility
As per the eligibility criteria of PRMO, Born on or after August 1, 1998 and All Indian students who are born on or after August 1, 1998 and, in addition, are in Class XI or below are eligible to appear for the PRMO 2017.A student from any state of the country can register for this examination and scholarship scheme. A student can be from a government or a private school.
Different Stages
Stage 1: Pre RMO (PRMO)
Details: Integer type questions (single or double digit) with 30 questions. It is organised by IAPT. Registration fee Rs. 200 at approved centres, Rs. 100 for KV Students.Students to be get carbon copy of OMR at the end of the paper.
Time duration: 2 hours 30 minutes, containing 30 subjective problems.
Exam Date: 20th August 2017
No of Selection: 300 per Regions, For KV CBSE, JNV Schools which have a countrywide coverage, the number to be selected is up to 5% of the number of the registration or 300.
Registration Period: From 10 May 2017 to 10 June 2017.
Result: 15 September 2017
——————————————————————————————————————————————————————
Stage 2: RMO (Regional Mathematics Olympiods)
Details: Each regional co-ordinator (including the co-ordinators for the groups KV, CBSE and JNV) will receive the list of students eligible to write RMO by September 15th 2017.
Time duration: 3 hours, containing 6 subjective problems.
Exam Date: 8th October 2017
No of Selection: 35 Students (30 Boys and 5 Girls) in each region.
Registration Period: No registration required. Regional coordinators will get the list of students of qualified Pre RMO 2017 who are eligible for RMO examination.
Result: 07 December 2017 by HBCSE
——————————————————————————————————————————————————————
Stage 3: INMO (Indian National Mathematical Olympiad)
Details: Only students selected on the basis of RMO(Regional Mathematical Olympiad) from different regions are eligible to appear for INMO (Indian National Mathematical Olympiad). Papers to be conducted by each regional coordinators and the papers are to be sent back to HBCSE.
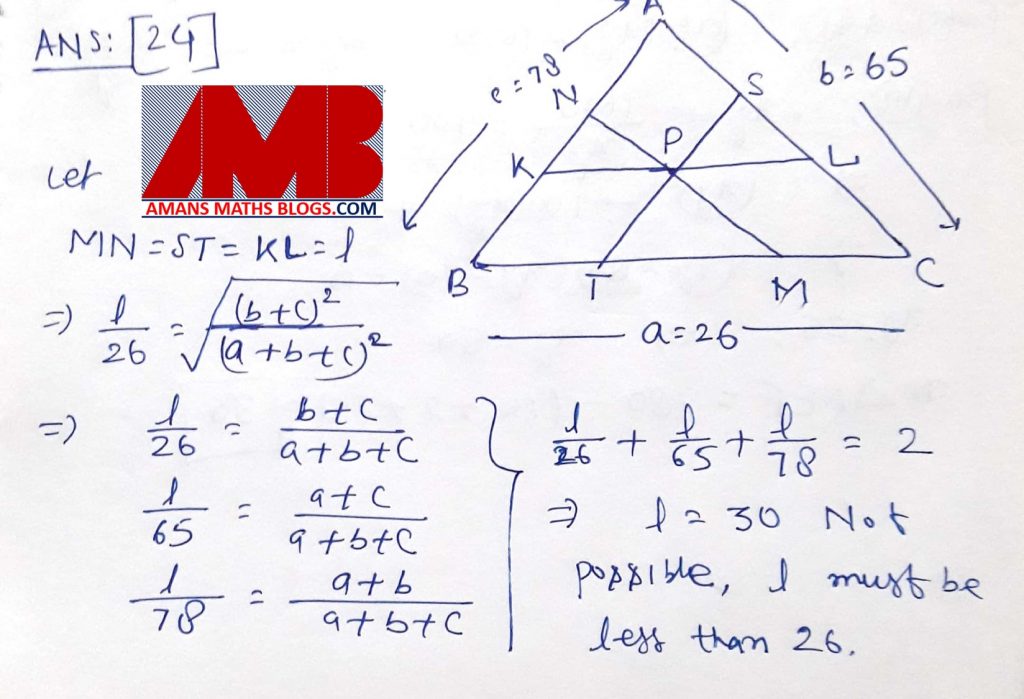
Time duration: 3 hours, containing 6 subjective problems.
Exam Date: 21st January 2018
No of Seats: About 30 students from each region are selected in the order of their merit. Approximately 900 students qualify for INMO.
Result: will be updated soon. Stay connected with us.
——————————————————————————————————————————————————————
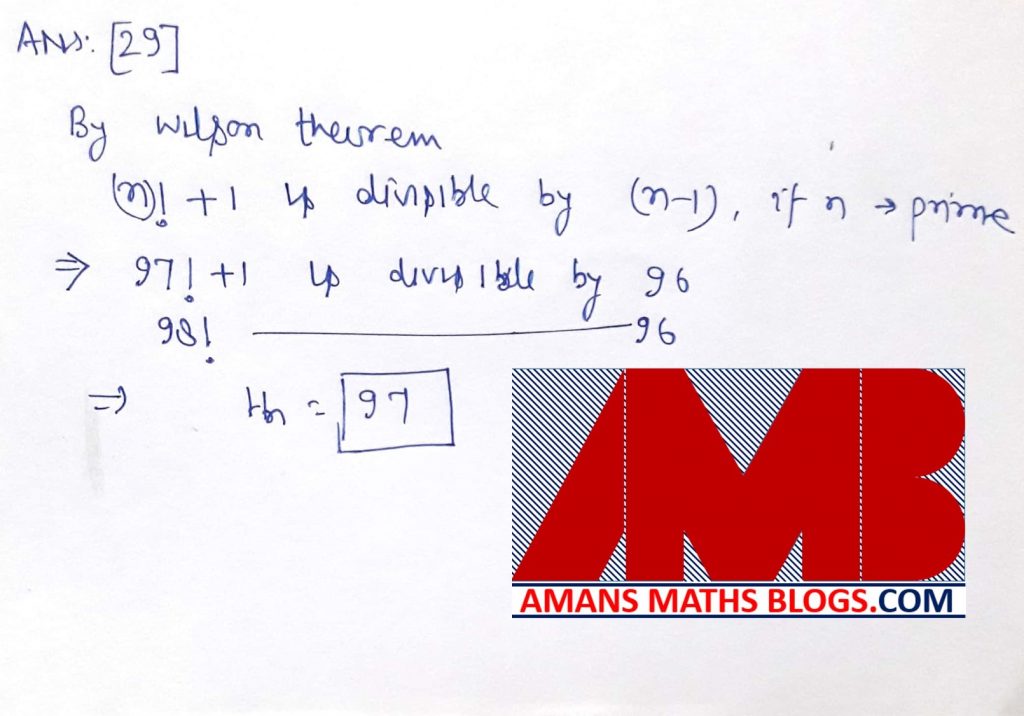
Stage 4: IMOTC (International Mathematical Olympiad Training Camp)
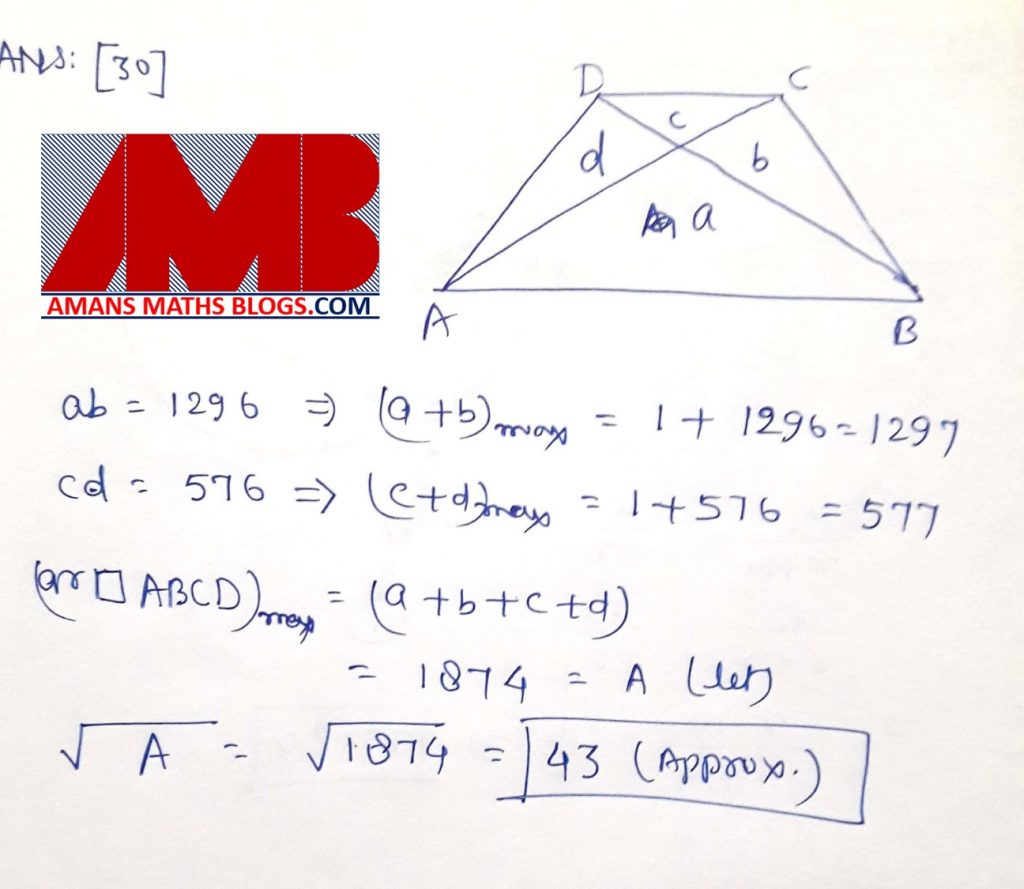
Details: The top 35-50 performers in INMO receive a certificate of merit. They are invited to a month long training camp (junior batch) conducted in May-June at Homi Bhabha Centre for Science Education (HBCSE), Mumbai. They undergo Lectures and Problem Solving sessions. In addition, INMO awardees of the previous year that have satisfactorily gone through postal tuition throughout the year are invited again for a second round of training (senior batch). The senior batch participants who successfully complete the camp receive a prize of Rs 5000 in the form of books and cash.
——————————————————————————————————————————————————————
Stage 5: PDT (Pre-Departure Training) Camp for IMO (International Mathematical Olympiad)
Details: The selected team of six students goes through another round of training and orientation for the about 10 days prior to the departure for IMO.
——————————————————————————————————————————————————————
Stage 6: IMO (International Mathematical Olympiad)
Details: The six members team selected at the end of the camp accompanied by a leader and deputy leader represent the country at the IMO, held in July each year in a different member country of IMO. Travel to IMO venue and return takes about two weeks. Students of Indian team who receive Gold, Silver, and Bronze medal at the IMO receive a cash prize of Rs. 5000, Re. 4000 and Rs .3000 respectively during the year following year at a formal ceremony at the end of the training camp.
Time duration: Two 4 hours 30 minutes written test on two days.
Exam Date: In July every year
Conducting BY:
PRE RMO– IAPT (www.iapt.org.in) through regional coordinators
RMO– Regional Coordinators
INMO– HBCSE (olympiads.hbcse.tifr.res.in)
Geographical Regions
Assam, Chattisgarh, Coastal AP & Rayalseema, Delhi, Gujarat- Daman-Diu-Dadra Nagar Haveli, Jammu, Jharkhand, Karnataka, Kerala, Madhya Pradesh, Maharashtra and Goa, Meghalaya, Mumbai, North Bihar and Patna, North Western States, Odisha, Rajasthan, South Bihar, Tamil Nadu, Telangana, Tripura, Uttar Pradesh, Uttarakhand, West Bengal.
Pre RMO Special Regions:
CBSE Schools, KV Schools, JNV Schools
Pre RMO Pattern/Syllabus
Syllabus for Mathematics Olympiads (regional, national and international) is class 9th to 12th standard mathematics.
The typical areas of problems are: Number Theory, Theory of Equation, Inequalities, Geometry, and Combinatorics.
The topics covered under these areas are: number systems, geometry, arithmetic of integers,quadratic equations and expressions, co-ordinate geometry, trigonometry,systems of linear equations, factorisation of polynomials, permutations and combinations,inequalities, probability theory,elementary combinatorics, number theory, complex numbers, elementary graph theory and , infinite series.
The syllabus does not include statistics and calculus. The difficulty level keeps increasing from RMO to INMO to IMO.
Pre RMO 2017 Question Paper:
The paper consisted of 30 questions of single or double digit integers to be solved in 150 minutes. The medium of test is English and regional languages. Each right answer carry one point each, thus making the total score of the candidate in a test equal to the number of questions answered correctly. There was no negative marking in the paper.
Read: Pre RMO and RMO Important Study Materials: Books | PDFs | Blogs | YouTube Channels | Solved Papers
Pre RMO 2017 Answer Keys:
| Q. No. | Answer | Q. No. | Answer | Q. No. | Answer |
|---|---|---|---|---|---|
| 1 | 28 | 11 | 60 | 21 | 48 |
| 2 | 73 | 12 | 60 | 22 | 36 |
| 3 | 16 | 13 | 24 | 23 | 47 |
| 4 | 25 | 14 | 10 | 24 | 30(BONUS) |
| 5 | 48 | 15 | 238 | 25 | 30 |
| 6 | 83 | 16 | 36 | 26 | 75 |
| 7 | 29 | 17 | 60/sqrt(7) (BONUS) | 27 | 20 |
| 8 | 7 | 18 | 21 | 28 | 28 |
| 9 | 60 | 19 | 36 | 29 | 97 |
| 10 | 48 | 20 | 73 | 30 | 43 |
Pre RMO 2017 Solution:
Ques 1: How many positive integers less than 1000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3 ?
Ques 2: Suppose a, b are positive real numbers such that 
.
Ques 3: A contractor has two teams of workers : team A and team B. Team A can complete a job in 12 days and team B can do the same job in 36 days. Team A starts working on the job and team B joins team A after four days. The team A withdraws after two more days. For how many more days should team B work to complete the job ?
Ques 4: Let a, b be integers such that all the roots of the equation (x2 + ax + 20)(x2 + 17x + b) = 0 are negative integers. What is the smallest possible value of a + b ?
Ques 5: Let u, v, w be real numbers in geometric progression such that u > v > w. Suppose u40 = vn = w60 . Find the value of n.
Ques 6: Let the sum written in its lowest terms be Find the value of q – p.
Ques 7: Find the number of positive integers n such that .
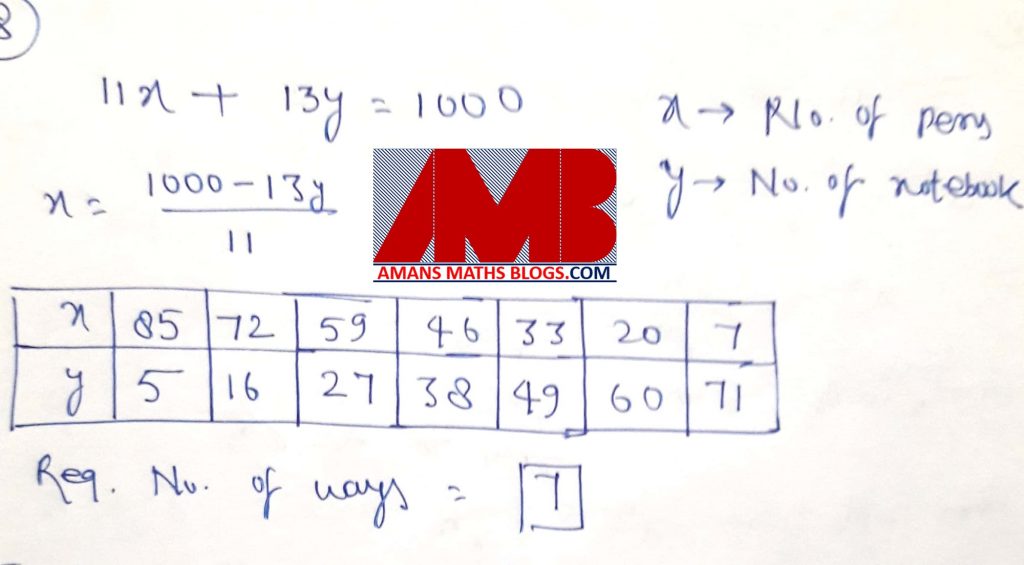
Ques 8 : A pen costs Rs 11 and a notebook costs Rs 13. Find the number of ways in which a person can spend exactly Rs 1000 to buy pens and notebooks.
Ques 9: There are five cities A,B,C,D,E on a certain island. Each city is connected to every other city by road. In how many ways can a person starting from city A come back to A after visiting some cities without visiting a city more than once and without taking the same road more than once ? (The order in which he visits the cities also matters. e.g., the routes are different.
Ques 10: There are eight rooms on the first floor of a hotel, with four rooms on each side of the corridor, symmetrically situated (that is each room is exactly opposite to one other room). Four guests have to be accommodated in four of the eight rooms (that is, one in each) such that no two guests are in adjacent rooms or in opposite rooms. In how many ways can the guests be accommodated?
Ques 11: Let for all real x. Find the least natural number n such that f(n + x) = f(x) for all real x.
Ques 12: In a class, the total numbers of boys and girls are in the ratio 4 : 3. On one day it was found that 8 boys and 14 girls were absent from the class and that the number of boys was the square of the number of girls. What is the total number of students in the class ?
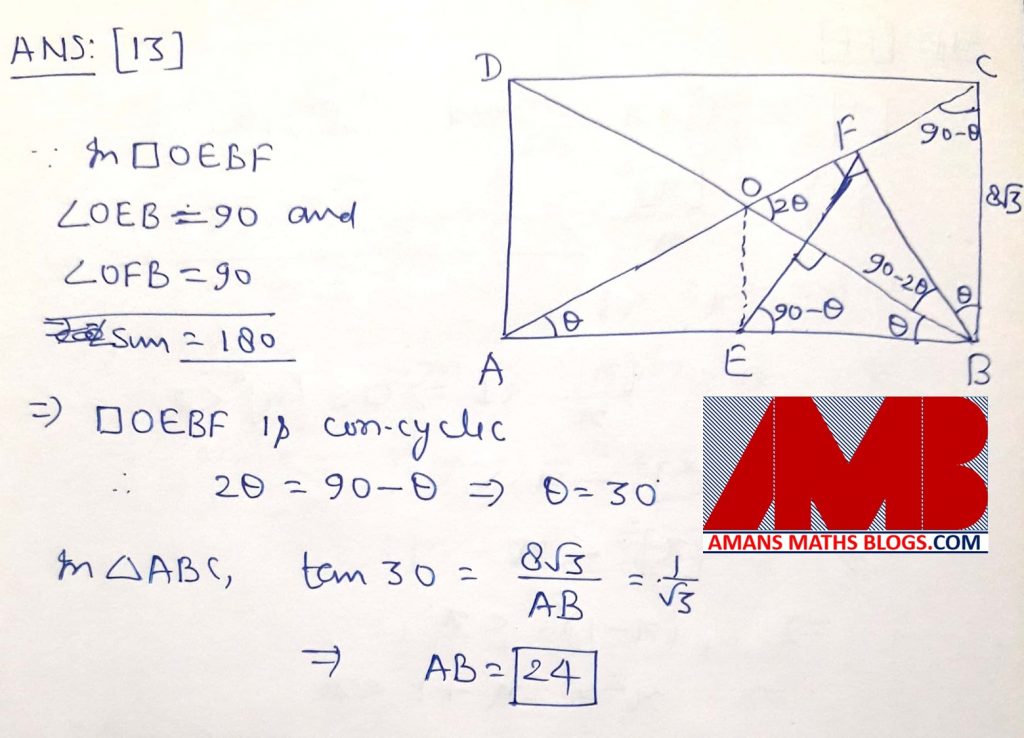
Ques 13 : In a rectangle ABCD, E is the midpoint of AB. F is point on AC such that BF is perpendicular to AC and FE perpendicular to BD. Suppose BC = . Find AB.
Ques 14: Suppose x is a positive real number such that {x}.[x] and x are in the geometric progression. Find the least positive integer n such that xn > 100. (Here [x] denotes the integer part of x and {x} = x – [x]).
Ques 15: Integers 1,2,3……..n where n > 2, are written on a board. Two numbers m, k such that 1 < m < n. 1 < k < n are removed and the average of the remaining numbers is found to be 17. What is the maximum sum of the two removed numbers ?
Ques 16: Five distinct 2-digit numbers are in a geometric progression. Find the middle term.
Ques 17: Suppose the altitudes of a triangle are 10,12 and 15. What is its semi-perimeter ?
Ques 18: If the real numbers x, y, z are such that x2 + 4y2 + 16z2 = 48 and xy + 4yz + 2zx = 24. what is the value of x2 + y2 + z2 ?
Ques 19: Suppose 1,2,3 are the roots of the equation x4 + ax2 + bx = c. Find the value of c.
Ques 20: What is the number of triples (a, b, c) of positive integers such that (i) a < b < c < 10 and (ii) a, b, c, 10 form the sides of a quadrilateral?
Ques 21: Find the number of ordered triples (a, b, c) of positive integers such that abc = 108.
Ques 22: Suppose in the plane 10 pair wise nonparallel lines intersect one another. What is the maximum possible number of polygons (with finite areas) that can be formed?
Ques 23: Suppose an integer x, a natural number n and a prime number p satisfy the equation 7x2 – 44x + 12 = pn. Find the largest value of p.
Ques 24: Let P be an interior point of a triangle ABC whose side lengths are 26, 65, 78. The line through P parallel to BC meets AB in K and AC in L. The line through P parallel to CA meets BC in M and BA in N. The line through P parallel to AB meets CA in S and CB in T. If KL, MN, ST are of equal lengths, find this common length.
Ques 25: Let ABCD be a rectangle and let E and F be points on CD and BC respectively such that area (ADE) = 16, area (CEF) = 9 and area (ABF) = 25. What is the area of triangle AEF ?
Ques 26: Let AB and CD be two parallel chords in a circle with radius 5 such that the centre O lies between these chords. Suppose AB = 6, CD = 8. Suppose further that the area of the part of the circle lying between the chords AB and CD is (m + n) / k, where m, n, k are positive integers with gcd(m, n, k) = 1. What is the value of m + n + k ?
Ques 27: Let 1 be a circle with centre O and let AB be diameter of 1. Let P be a point on the segment OB different from O. Suppose another circle 2 with centre P lies in the interior of 1. Tangents are drawn from A and B to the circle 2 intersecting 1 again at A1 and B1 respectively such that A1 and B1 are on the opposite sides of AB. Given that A1 B = 5, AB1 = 15 and OP = 10, find the radius of 1.
Ques 28: Let p, q be prime numbers such that n3pq – n is a multiple of 3pq for all positive integers n. Find the least possible value of p + q.
If you know the solution of this question, then comment the subjective solution.
Ques 29: For each positive integer n, consider the highest common factor hn of the two numbers n! + 1 and (n + 1)!. For n < 100, find the largest value of hn.
Ques 30: Consider the areas of the four triangles obtained by drawing the diagonals AC and BD of a trapezium ABCD. The product of these areas, taken two at time, are computed. If among the six products so obtained, two product are 1296 and 576, determine the square root of the maximum possible area of the trapezium to the nearest integer.
