Real Life Application of Logarithms Its Implementation Example

Hi Students, welcome to Amans Maths Blogs (AMB). In this article, you will get an idea of “Real Life Scenario of Logarithm”. Real life scenario of logarithms is one of the most crucial concepts in our life.

As we know, in our maths book of 9th-10th class, there is a chapter named LOGARITHM is a very interesting chapter and its questions are some types that are required techniques to solve.

Therefore, you must read this article “Real Life Application of Logarithms” carefully.

Table of Contents

Usage of Logarithms

Definition of Logarithms:

Logarithms, often abbreviated as “logs,” are mathematical functions that represent the inverse operation of exponentiation. In simpler terms, logarithms provide a means to reverse the process of raising a number to a certain power.

The logarithm of a number with respect to a given base is the exponent to which the base must be raised to produce that number. Mathematically, it can be represented as:

y = log_ax, where y is the logarithm of x to the base a.

Logarithms are commonly used to solve exponential equations, find unknown exponents, and express large or small numbers in more manageable forms.

Understanding this fundamental definition sets the stage for exploring the myriad applications of logarithms across various fields, where their ability to simplify complex calculations and represent exponential relationships proves invaluable.

Apart from Real Life Application of Logarithms, you can also clear you following doubts:

Doubt 1: Why the function f(x) = 0^x is NOT an exponential function.

Doubt 2: Why the function g(x) = 1^x is NOT an exponential function.

Doubt 3: Why the function h(x) = (–2)^x is NOT an exponential function.

Doubt 4: Why the base of logarithm cannot be negative, means a > 0?

Doubt 5: Why the base of logarithm cannot be unity, means a ≠ 1?

Doubt 6: Why the logarithm of any negative number is not defined, mean log(–2) is not defined?

Types of Logarithms:

Logarithms come in several types, each with its own base, commonly denoted as ‘ $a’$ . The most widely used types of logarithms include:

Common Logarithms (Base = 10)

Common logarithms have a base of 10 and are denoted as $log (x)$ or $log_{10} (x)$ .

It means, if the base is not mentioned in log, then you need to use base as ’10’. Logarithms are extensively utilized in various scientific calculations and engineering applications.

For instance, common logarithms are employed in seismic studies to measure earthquake magnitudes on the Richter scale, where each increase of one unit represents a tenfold increase in seismic amplitude.

Natural Logarithms (Base = e)

Natural logarithms have a base of the mathematical constant ‘ $e’$ , approximately equal to 2.71828, and are denoted as $ln (x)$ .

They arise naturally in exponential growth and decay problems, as well as in calculus and mathematical modeling.

Natural logarithms find applications in finance, biology, and physics, aiding in the analysis of exponential processes and growth rates.

Binary Logarithms (Base = 2)

Binary logarithms, also known as logarithms to the base 2, are denoted as $log_{2} (x)$ .

They are prevalent in computer science and information theory, particularly in analyzing binary data and calculating the complexity of algorithms.

Binary logarithms help quantify the number of bits required to represent integers or the efficiency of binary search algorithms.

Logarithmic Rules:

Understanding the fundamental rules governing logarithms is essential for effectively manipulating and simplifying expressions involving logarithmic functions. Here are some key logarithmic rules:

Logarithm Product Rules

The product rule states that the logarithm of a product is equal to the sum of the logarithms of the individual factors. Mathematically, it can be expressed as:

log_a(mn)=log_a(m)+log_a(n)

This rule allows us to break down complex products into simpler logarithmic expressions, facilitating calculations and problem-solving.

Logarithm Quotient Rules

The quotient rule dictates that the logarithm of a quotient is equivalent to the difference of the logarithms of the numerator and denominator. In equation form:

log_a(m / n)=log_a(m) – log_a(n)

This rule enables us to decompose division operations into more manageable logarithmic terms, simplifying computations.

Logarithm Power Rules

The power rule states that the logarithm of a number raised to a power is equal to the exponent multiplied by the logarithm of the base. Mathematically, it can be represented as:

log_a(mⁿ)=nlog_a(m)

This rule facilitates the handling of exponential expressions within logarithmic functions, allowing for efficient manipulation and evaluation.

Logarithm Change of Base Formula

The change of base formula provides a method for converting logarithms from one base to another. It states that the logarithm of a number in a certain base can be expressed as the quotient of logarithms in different bases. The formula is given by:

log_a(x)=log_c(x) / log_c(a)

where ‘c’ can be any base. This formula is particularly useful when dealing with logarithms in bases other than the commonly encountered bases of 10 and e.

Logarithm to Exponential and Exponential to Logarithm:

Expressing Logarithms to Exponentials

Logarithms can be expressed as exponentials using the definition of logarithms.

If $y = log_{a} (x)$ ,

then the logarithmic equation can be rewritten in exponential form as

x = a^y.

Expressing Exponentials to Logarithms

Exponentials can be expressed as logarithms using the inverse relationship between logarithms and exponentials.

If x = a^y,

then the logarithmic equation can be rewritten in exponential form as

$y = log_{a} (x)$ .

Real Life Applications of Logarithms

From measuring the intensity of earthquakes to calculating the pH levels of substances, logarithms offer a powerful tool for simplifying complex calculations and understanding exponential relationships.

In this discussion, we will explore several compelling real-life applications of logarithms, demonstrating how this mathematical concept plays a crucial role in various fields such as science, finance, and technology.

Applications of Logarithms: Measuring Sound Intensity Using Decibel

Definition of Decibels

Decibels are a unit of measurement used to express the relative intensity of sound. The decibel scale is logarithmic, with each increase of 10 dB representing a tenfold increase in sound intensity.

Mathematically, the relationship between sound intensity ‘I’ and sound level in decibels $L$ can be expressed as:

L = 10^.log₁₀(I / I₀)

where I $_{0}$ is the reference intensity level (usually set at the threshold of human hearing, approximately $1 0^{-12}$ watts per square meter).

Applications in Noise Measurement:

Decibels are commonly used to measure noise levels in various environments, such as workplaces, urban areas, and transportation hubs.

By quantifying sound intensity on a logarithmic scale, decibels allow for a more nuanced assessment of noise pollution and its potential impact on human health and well-being.

Regulatory agencies often set noise exposure limits based on decibel measurements to mitigate the adverse effects of excessive noise.

Sound Engineering and Music Production:

In sound engineering and music production, decibels are used to calibrate audio equipment, determine optimal sound levels, and control the balance between different audio components.

Engineers and producers rely on decibel measurements to achieve desired sound quality, dynamic range, and clarity in recordings and live performances.

Decibels also play a crucial role in audio mastering and mixing processes, ensuring consistent sound levels across different tracks and audio sources.

Applications of Logarithms: Stock Market Analysis

Percentage Changes and Returns:

Logarithms are commonly used to calculate percentage changes and returns in stock prices.

By taking the logarithm of the ratio of current price to previous price, analysts can determine the logarithmic return, which represents the percentage change in price over a given period.

Logarithmic returns provide a more symmetrical and interpretable measure of price changes, particularly for volatile assets, and are widely used in financial modeling and risk management.

Volatility Measurement:

Logarithms are instrumental in measuring volatility, a key parameter in assessing risk and investment performance. Volatility, often quantified using standard deviation or variance, reflects the magnitude of price fluctuations in financial markets.

Logarithmic returns are used to calculate volatility metrics such as historical volatility and implied volatility, which help investors gauge the level of uncertainty and potential price movements in the market.

Technical Analysis:

In technical analysis, logarithms are employed to transform price series and indicators to achieve stationarity and normalize data distributions.

Common transformations include taking the natural logarithm of prices or volume measures to stabilize variance and remove trends.

Logarithmic transformations facilitate the application of statistical techniques and pattern recognition algorithms, enabling traders to identify trends, support and resistance levels, and trading signals more effectively.

Portfolio Optimization:

Logarithms are utilized in portfolio optimization techniques to model asset returns and correlations.

By transforming asset returns into logarithmic space, analysts can linearize the relationship between asset returns and portfolio returns, making optimization models more tractable.

Logarithmic transformations also allow for the application of mean-variance analysis and modern portfolio theory, guiding investors in constructing diversified portfolios that balance risk and return objectives.

Applications of Logarithms in Decay of Radioactive Elements

Logarithms are fundamental in understanding and modeling the decay of radioactive elements, a process governed by exponential decay kinetics. Here’s how logarithms are applied in the study of radioactive decay:

Decay Law:

The decay of radioactive elements follows a predictable pattern described by the decay law. The decay rate, commonly denoted as $λ$ , represents the probability of a radioactive nucleus decaying per unit time.

The number of radioactive nuclei remaining after a certain time $t$ can be expressed using the exponential decay equation:

N(t) = N₀^.e^– $λt,$

$where N (t) is the number of radioactive nuclei at time t, N_{0} is the initial number of nuclei, and e is the base of the natural logarithm. Logarithms come into play when solving for unknown variables such as decay rate or time elapsed, as well as interpreting experimental data.$

Half Life Calculuation:

Logarithms are instrumental in determining the half-life ( $T_{1/2}$ ) of a radioactive element, which is the time required for half of the radioactive nuclei to decay. The half-life can be derived from the decay constant ( $λ$ ) using the relationship:

T1/2 = ln(2) / $λ$

$By taking the natural logarithm of both sides of the decay equation, scientists can isolate the decay constant and calculate the half-life, a crucial parameter in radiometric dating and nuclear medicine.$

Activity Measurement:

Logarithms are used to quantify the activity of radioactive samples, which represents the rate of decay or the number of decays per unit time.

The activity ( $A$ ) of a radioactive sample can be calculated using the equation: A = $λ . N$

$where λ is the decay constant and N is the number of radioactive nuclei.$

$Logarithmic transformations enable scientists to convert activity measurements into meaningful units such as becquerels (Bq) or curies (Ci), facilitating comparisons and regulatory compliance.$

Applications of Logarithms in Radiocarbon Dating

$Radiocarbon dating is a widely used technique for determining the age of archaeological artifacts and geological samples containing organic material.$

$Logarithms play a crucial role in radiocarbon dating calculations and interpretations. Here’s how logarithms are applied in radiocarbon dating:$

Decay of Carbon-14:

Radiocarbon dating relies on the radioactive decay of carbon-14 ( $^{14} C$ ), a naturally occurring isotope of carbon.

Carbon-14 undergoes radioactive decay by emitting a beta particle, transforming into nitrogen-14 ( $^{14} N$ ).

The decay process follows exponential decay kinetics, where the rate of decay is proportional to the number of radioactive nuclei present.

Half-Life of Carbon-14:

The half-life of carbon-14 is approximately 5,730 years, meaning that it takes 5,730 years for half of the carbon-14 atoms in a sample to decay into nitrogen-14.

Logarithms are employed to calculate the age of a sample based on the ratio of carbon-14 to stable carbon-12 ( $^{12} C$ ) isotopes.

By measuring the remaining ratio of carbon-14 to carbon-12 and applying the exponential decay equation, scientists can determine the age of the sample.

Libby’s Law:

Radiocarbon dating calculations are based on Libby’s Law, which relates the activity of carbon-14 in a sample to its age.

The activity ( $A$ ) of carbon-14 is proportional to the number of radioactive nuclei present, following the equation:

A(t) = A₀^.e^– $λt,$

$where A_{0} is the initial activity of the sample, t is the age of the sample, and λ is the decay constant of carbon-14.$

$Logarithms are used to solve for the age of the sample (t) by rearranging the equation and isolating the variable of interest.$

Application of Logarithms in Measuring Earthquakes Using the Richter Scale:

$The Richter scale, developed by Charles F. Richter in 1935, is a logarithmic scale used to measure the magnitude of earthquakes.$

$Logarithms play a crucial role in quantifying and comparing the seismic energy released by earthquakes. Here’s how logarithms are applied in measuring earthquakes using the Richter scale:$

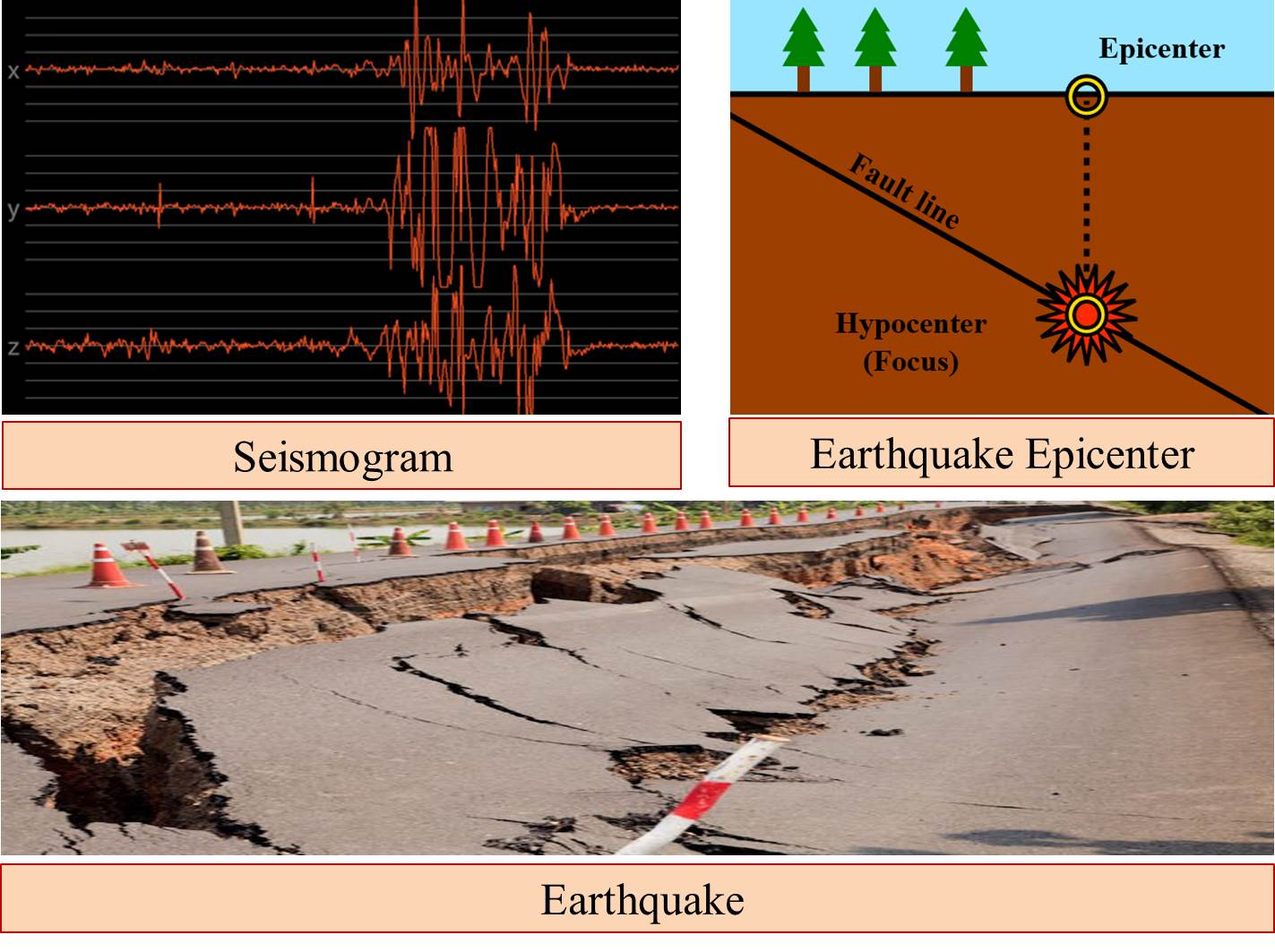
Definition of Magnitude:

The magnitude of an earthquake is a measure of the energy released at the earthquake’s source.

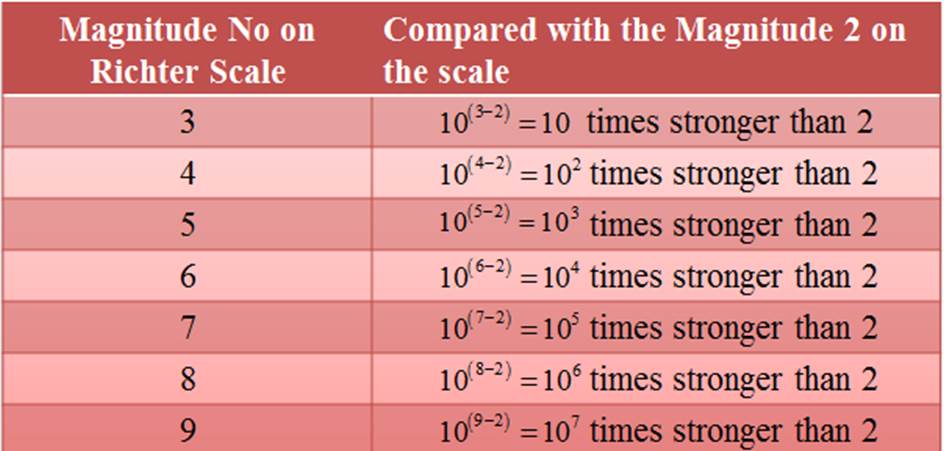
The Richter scale measures this energy logarithmically, with each whole number increase on the Richter scale representing a tenfold increase in amplitude of seismic waves and approximately 31.6 times more energy release.

Mathematically, the Richter magnitude $M$ of an earthquake is calculated using the equation: M = 10^.log₁₀(A / A₀),

where $A$ is the maximum amplitude of seismic waves recorded on a seismogram and $A_{0}$ is a reference amplitude.

For example: if we note the magnitude of the earthquake on the Richter scale as 2, then the other next magnitude on the scale is explained in the following table.

Now according to the Richter scale magnitude of the earthquake, there is a lot of bad effect on our environments which may be a danger to the real world. Its details are given below in the table.

Richter Magnitude	Description	Earthquake Effects
0-2.0	Micro	Never Felt by People
2.0-2.9	Minor	Felt But Not Recorded
3.0-3.9	Minor	Felt But Not Damaged Cost
4.0-4.9	Light	Ceiling Lights Swing But Not Damaged
5.0-5.9	Moderate	Affects weak construction and cause wall crack
6.0-6.9	Strong	Affects area up to 160 km from the epicenter
7.0-7.9	Major	Affect area up to further area and cause several damaged
8.0-8.9	Great	Affect area beyond 100 miles and cause severe damaged
9.0-9.9	Great	Affect area beyond 1000 miles with disastrous effects
10+	Epic	Never Been Recorded

This is one of the real-life scenario of logarithms, which must be known.

Logarithmic Representation:

Logarithms allow for the concise and intuitive representation of seismic energy on a logarithmic scale.

By taking the logarithm of the ratio of seismic wave amplitudes, the Richter magnitude compresses a wide range of energy levels into a manageable scale.

This logarithmic representation enables scientists to compare earthquakes of different magnitudes and assess their relative impact on structures and communities.

Sensitivity to Energy Release:

The logarithmic nature of the Richter scale makes it highly sensitive to small changes in seismic energy. Even minor increases in earthquake magnitude result in significant jumps in the measured Richter magnitude.

For example, a magnitude 6.0 earthquake releases ten times more energy than a magnitude 5.0 earthquake, while a magnitude 7.0 earthquake releases a thousand times more energy than a magnitude 5.0 earthquake. Logarithmic scaling ensures that the Richter scale captures the full range of seismic energy released by earthquakes.

Application of Logarithms in Measuring pH Levels of Chemicals

$The pH scale is a logarithmic scale used to measure the acidity or alkalinity of a solution.$

$Logarithms play a fundamental role in quantifying pH levels and understanding the behavior of acidic and basic substances.$

$Here’s how logarithms are applied in measuring pH levels of chemicals:$

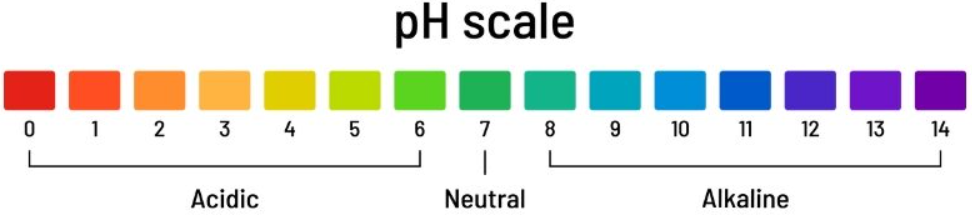
Definition of pH:

pH is a measure of the concentration of hydrogen ions ( $H^{+}$ ) in a solution.

The pH scale ranges from 0 to 14, with a pH of 7 considered neutral, pH values below 7 indicating acidity, and pH values above 7 indicating alkalinity.

The pH of a solution is calculated using the negative logarithm of the hydrogen ion concentration ( $[H^{+}]$ ) in moles per liter ( $mol/L$ ):

pH = -log₁₀[H⁺]

Logarithms are essential for transforming the hydrogen ion concentration into a more manageable scale, enabling the quantification of acidity and alkalinity on a numerical scale.

Logarithmic pH Scaling:

Logarithms compress the wide range of hydrogen ion concentrations found in solutions into a scale that is easily interpreted and compared.

Each unit change in pH represents a tenfold change in hydrogen ion concentration.

For example, a solution with a pH of 5 has 10 times more hydrogen ions than a solution with a pH of 6 and 100 times more hydrogen ions than a solution with a pH of 7.

Logarithmic scaling ensures that small changes in acidity or alkalinity result in significant changes in pH, making the scale sensitive to variations in solution chemistry.

Practical Applications:

The logarithmic nature of the pH scale has numerous practical applications in various industries and fields. In chemistry, pH measurements are crucial for assessing the reactivity and stability of chemical compounds, controlling chemical processes, and maintaining optimal conditions for biological systems.

In environmental science, pH measurements are used to monitor water quality, assess pollution levels, and study the health of aquatic ecosystems. In agriculture, pH measurements guide soil management practices and fertilizer application, ensuring optimal nutrient availability for plant growth.

Application of Logarithms in Calculating Population Growth:

$Logarithms are instrumental in modeling and analyzing the growth of human populations and other living species. Through population dynamics models, logarithms provide valuable insights into population growth rates, carrying capacities, and sustainability.$

$Here’s how logarithms are applied in calculating the growth of human species or other living species:$

Exponential Growth Model:

Logarithms are closely associated with exponential growth, a common model used to describe population growth in ideal conditions.

The exponential growth model assumes that populations grow at a constant percentage rate over time. Mathematically, the exponential growth equation is expressed as:

N(t) = N₀^.e^r $t,$

$where N (t) is the population size at time t, N_{0} is the initial population size, r is the per capita growth rate, and e is the base of the natural logarithm.$

$Logarithms enable scientists to transform exponential growth equations into linear forms for analysis and interpretation.$

Logistic Growth Model:

The logistic growth model incorporates limitations on population growth, such as finite resources and environmental constraints.

Unlike exponential growth, logistic growth accounts for carrying capacity, the maximum population size that a habitat can support sustainably. The logistic growth equation is given by

N(t) = K / [1 + (K – N₀) / N₀ * e^-rt]

where $K$ is the carrying capacity of the environment.

Logarithms play a role in solving logistic growth equations and analyzing population dynamics near carrying capacity.

Doubling Time and Half-Life:

Logarithms are used to calculate doubling time and half-life in population growth scenarios.

Doubling time represents the time required for a population to double in size under exponential growth conditions.

It is calculated using the formula:

T_double = ln(2) / r

where $r$ is the growth rate. Similarly, half-life represents the time required for a population to reach half of its maximum size under logistic growth conditions. It is calculated using logarithms and the logistic growth equation.

Applications of Logarithms in Analyzing Drug Concentration:

$Logarithms play a crucial role in pharmacokinetics, the study of how drugs are absorbed, distributed, metabolized, and excreted in the body.$

$Logarithmic transformations are commonly used to analyze drug concentration data and understand the pharmacological behavior of medications.$

$Here’s how logarithms are applied in analyzing drug concentration in medicines:$

Pharmacokinetic Models:

Pharmacokinetic models describe the time course of drug concentration in the body following administration.

These models typically involve exponential decay (for drug elimination) or exponential increase (for drug absorption) of drug concentration over time.

Logarithmic transformations are used to linearize pharmacokinetic data and facilitate the estimation of pharmacokinetic parameters such as clearance, volume of distribution, and half-life.

Linear Pharmacokinetic Models:

In linear pharmacokinetics, drug concentration changes proportionally with dose and time.

Logarithmic transformations are applied to linearize drug concentration-time profiles, allowing for the calculation of pharmacokinetic parameters using linear regression analysis.

For example, the elimination rate constant ( $k_{el}$ ) can be estimated from the slope of the linear portion of the drug concentration-time curve, which is obtained after logarithmic transformation.

Non-Linear Pharmacokinetic

In nonlinear pharmacokinetics, drug concentration changes non-proportionally with dose or time due to saturation of drug-metabolizing enzymes or transporters.

Logarithmic transformations are used to transform nonlinear pharmacokinetic data into linear form, enabling the application of linear regression techniques to estimate parameters such as Michaelis-Menten constants ( $K_{m}$ ) and maximum rate of metabolism ( $V_{max}$ ).

Drug Bioavailability and Bioequivalence:

Logarithmic transformations are employed in the assessment of drug bioavailability and bioequivalence.

Bioavailability measures the fraction of an administered drug that reaches systemic circulation unchanged, while bioequivalence compares the pharmacokinetic parameters of different formulations of the same drug.

Logarithmic transformations are used to assess the extent and rate of drug absorption, enabling comparisons between different formulations or routes of administration.

Read More : 129 Maths Short Tricks

Applications of Logarithms in Calculating Complex Values

Sometimes we need to find the values of some complex calculations like x = (31)^(1/5) (5th root of 31), finding a number of digits in the values of (12)^256 etc. To solve these types of problems, we need to use the logarithms.

The solving method of these problems will be learning in another maths blogs post. The URL of the post will be mentioned below in the future.

Practice: Logarithm Questions Set 1

Applications of Logarithms in Compound Interest:

$Logarithms are fundamental in understanding and calculating compound interest, a concept central to finance and investment.$

$Compound interest refers to the interest earned not only on the initial principal amount but also on the accumulated interest from previous periods.$

$Logarithms play a crucial role in determining the future value of investments, amortizing loans, and evaluating investment performance.$

$Here’s how logarithms are applied in compound interest calculations:$

Compound Interest Formula:

The compound interest formula calculates the future value ( $F V$ ) of an investment or loan, taking into account the initial principal ( $P$ ), the annual interest rate ( $r$ ), the number of compounding periods per year ( $n$ ), and the time in years ( $t$ ). The formula is given by:

FV = P x (1 + r/100)^nt

Logarithms are used to solve for any unknown variable in the compound interest formula, such as the principal, interest rate, compounding frequency, or time.

Continuous Compounding:

Logarithms facilitate the calculation of compound interest under continuous compounding, where interest is compounded infinitely often over time. The formula for continuous compounding is:

FV = P x e^rt

where $e$ is the base of the natural logarithm. Logarithms enable the transformation of continuous compounding equations into more manageable forms and allow for comparisons with compound interest calculations using discrete compounding periods.

Time Value of Money:

Logarithms are used to calculate the present value ( $P V$ ) of future cash flows or the future value ( $F V$ ) of present investments, taking into account the time value of money.

By discounting future cash flows back to their present value using logarithmic transformations, investors can make informed decisions about the profitability and riskiness of investment opportunities.

Amortization of Loans:

Logarithms are employed in loan amortization schedules to calculate the periodic payments required to repay a loan over time.

By decomposing the total payment into principal and interest components using logarithmic transformations, borrowers can understand the distribution of payments and the impact of different repayment schedules on the total cost of borrowing.

Difference Between Algorithms and Logarithms

Algorithms and logarithms are both fundamental concepts in mathematics and computer science, but they serve different purposes and have distinct characteristics. Here’s a comparison between algorithms and logarithms:

Algorithms vs Logarithms: Difference 1#

Algorithm: An algorithm is a step-by-step procedure or set of rules for solving a problem or performing a specific task. Algorithms can be expressed in natural language, pseudocode, or programming languages and are used to automate processes and achieve desired outcomes.

Logarithm: A logarithm is a mathematical function that represents the exponent to which a fixed number, called the base, must be raised to produce a given number. Logarithms are used to solve exponential equations, transform data, and quantify relationships between variables.

Algorithms vs Logarithms: Difference 2#

Algorithm: Algorithms are used to solve computational problems, automate tasks, and optimize processes. They are widely used in computer science, engineering, data analysis, and various other fields to perform calculations, manipulate data, and make decisions.

Logarithm: Logarithms are used primarily in mathematics and science to simplify calculations, express relationships between variables, and solve exponential equations. They have applications in fields such as finance, chemistry, physics, and biology for modeling natural phenomena and analyzing data.

Algorithms vs Logarithms: Difference 3#

Algorithm: Algorithms can be represented in various forms, including pseudocode, flowcharts, and programming code. They specify a sequence of steps or instructions to be followed to solve a problem or achieve a specific objective.

Logarithm: Logarithms are represented using mathematical notation, typically written as ( $log_{b} (x))$ , where $b$ is the base and $x$ is the number whose logarithm is being calculated. Common bases include 10 (common logarithm) and $e$ (natural logarithm).

Algorithms vs Logarithms: Difference 4#

Algorithm: Algorithms are used to design software applications, develop algorithms for solving complex problems, implement data structures and algorithms, and optimize processes in various domains.

Logarithm: Logarithms are used in mathematical calculations, scientific research, engineering analysis, financial modeling, and statistical analysis. They help simplify mathematical expressions, quantify relationships between variables, and solve exponential equations.

FAQ (Frequently Asked Questions) on Real Life Application of Logarithms

How are logarithms used in engineering?

In engineering, all the two types of logarithms known as common logarithm and natural logarithm, are used. In chemical engineering, logarithms are used to measure radioactive decay and pH solutions. In biomedical engineering, logarithms are used to measure cell decay and growth.

How are logarithms used in finance?

In finance, the logarithms is used in quantitative finance (specially in CFA Level 1, 2, 3 Exams). Here, the base of the logarithm is e (exponential). By using log of any number on base e, we can compute continuously compounded returns.

What is log10 equal to?

If the base of the log is 10, then the value of log₁₀10 = 1 using the formula of log_aa = 1. If the base of the log is e, then the value of log_e10 = 2.302585.

application of logarithm in real life application of logarithms in real life situations application of logarithms in real life situations pdf logarithm in real life logarithmic function in real life logarithmic function real life examples logarithmic functions in real life logarithmic real life examples real life application of logarithmic function real life example of logarithmic function real life examples of logarithmic functions real life logarithmic functions richter scale formula