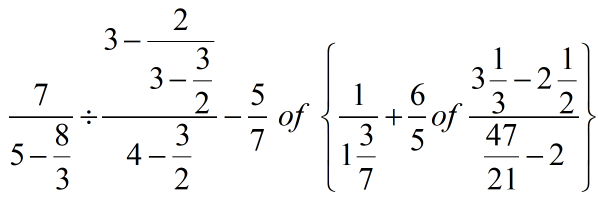Hi students, welcome to Amans Maths Blogs (AMB). Are you an aspirant of any competitive exams like CBSE Board, JEE, NTSE, NDA, NMTC etc.? If yes, then it is very important to solve the previous year questions papers to get the knowledge of the paper pattern of that particular examination. So, in this article, the students will get the NMTC final stage previous year question papers for class 5 and 6. These NMTC final stage previous year question papers are important for those students who qualify the NTSE Stage 1 exam.
Get Sample Paper for NMTC Stage 1 Primary Level
Now, the question is why it is important to solve NMTC final stage previous year question papers for class 5 and 6.
This is because solving the NMTC stage 2 previous year question papers will help the aspirants of NMTC to get the blend knowledge and depth of the concepts and solve those tricky questions quickly.
As NMTC is conducted by AMTI, it is a national level tests. It is very important for the aspirants to get extremely go through the whole syllabus and paper pattern and this is the most important benefit of solving previous year question papers of NMTC stage 2.
On solving these NMTC final stage previous year question papers for class 5 and 6, the candidates understand the important topics and identify their weak areas of whole syllabus.
By solving the NMCT stage 2 previous year question papers, the candidates get the speed and accuracy of solving questions and also get the fair idea about the paper pattern.
It helps the aspirants about the marking scheme, time management to solve the tricky questions. The aspirants can solve the NMCT stage 2 previous year question paper and analyse their preparation level of the exams.
Solving practice papers and NMTC final stage previous year question papers for class 5 and 6 also a great way to revise the whole syllabus and test your grip cover about the topics.
Click Here NMTC 2019 Notification
Before starting the preparation of NMTC final stage, the students must be aware the exam pattern and structure of NMTC exams. This will help the aspirants to prepare their preparation path.
NMTC final stage previous question paper will help the aspirants together a fair idea about the difficulty level of different sections of NMTC.
The aspirants must practice the NMTC final stage previous year question papers for class 5 and 6 in order to get the exams pattern of NMTC final stage.
These previous year question papers will help the candidate to learn about the trending topics and most of the frequently asked questions type in the exams.
Solving NMTC stage 2 previous year question papers also help the students to know their weak areas in the whole syllabus and work on them.
We know that there are three following factors in any competitive exams and that are speed of solving tricky questions, time management skills and accuracy or efficiency of solving questions. These three factors are very important in any exams. To masters in these factors, the students must try to solve the NMTC final stage previous year question papers for class 5 and 6.
NMTC Final Stage Previous Year 2010 Question Papers For Class 5 and 6
Instructions:
- Answer as many questions as possible.
- Elegant and novel solutions will be get extra credits.
- Diagram and explanations should be given wherever necessary.
- Fill in FACE SLIP and your rough working should be in the answer book.
- Maximum time allowed time is 3 hours.
- All questions carry equal marks.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 1
Given two numbers say 1 and 2, the addition problems is: 1 + 2 (or 2 + 1). Thus, there is just one addition problem. (Considering 1 + 2 and 2 + 1 as the same). Given three numbers 1, 2 and 3, the number of addition problems are 1 + 2 + 3; 12 + 3; 21 + 3; 31 + 2; 13 + 2; 32 + 1 and 23 + 1. Thus, there are 7 addition problems. Using all the four numbers 1, 2, 3, 4 list all the two digit-two added addition problems. Find the sum in each case. What is maximum sum and minimum sum?
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 2
A four-digits number of the form abab, a ≠ b, a, b ≠ 0 (and a, b are the digits of the 4 digit number) is called a rectangular number.
(a) How many 4 digit rectangular numbers are there?
(b) What is the GCD of all these rectangular numbers?
(c) If these 4-digit numbers represent the area of rectangles, find the sides of the rectangle with minimum area. Find also the maximum perimeter of this rectangle.
(d) Find the sides of the rectangle with the biggest area and also find the least perimeter of this rectangle.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 3
The odd numbers are arranged in groups as follows {1}, {3, 5}, {7, 9, 11}, {13, 15, 17, 19}, … What is the average of the numbers appearing in the 20th group?
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 4
ABC is an equilateral triangle of side 12 cm. BC, CA and AB are trisected (divided into three equal parts) at the points (P, Q), (R, S) and (T, U) respectively.
(a) Calculate the sides and angles of the hexagon (six sides figure) PQRSTU.
(b) If the six points P, Q, R, S, T and U are taken on the sides BC, CA and AB of the same equilateral triangle such that BP = QC = CR = SA = AT = UB = 2 cm, then find the measure of the sides and angles of this hexagon PQRSTU.
(c) In the same equilateral triangle if the six points P, Q, R, S, T, and U taken as mentioned above such that BP = CR = AT = 1 cm and QC = SA = UB = 2 cm. Find the measure of the sides and angles of the hexagon PQRSTU.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 5
a, b, c are three natural numbers in ascending order laying between 30 and 40. Given (a + b), (b + c) and (c + a) are not divisible by 3. Find all such triples (a, b, c). Find the sums in each case. Which of the sums are is divisible by 3?
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 6
Six seats are vacant on and straight bench. Find the number of ways three students Amala, Bhanu and Ghander occupy three seats so that Amala and Bhanu do not sit together.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 7
In the sequence 6, 14, 8, –6, … , every term after the second is the difference of the preceding term in the reverse order. Find the sum of the first 2010 terms.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 8
An ascending integer is one in which each digit greater than any other digit which precedes it (Example: 359). How many ascending integers are there between 200 and 300?
NMTC Final Stage Previous Year 2011 Question Papers For Class 5 and 6
Instructions:
- Same as previous instructions.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 1
Nivisha of standard six bought a book. On the first day she read one-fifth of the number of pages of the book plus 12 pages. On the second day, she read one fourth of the remaining pages plus 15 pages and on the third day she read one third of the remaining pages plus 20 pages. The fourth day which is the final day she read the remaining 60 pages of the book and completed reading. Find the total number of the pages in the book and the number of the pages read on each day.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 2
In the adjoining figure ΔABC, ∠ A is equal to an angle of an equilateral triangle.
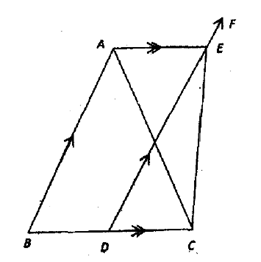
The line DEF is parallel to AB and AE is parallel to BC. ∠ CEF = 170° and ∠ ACE = ∠ B + 10°. Find the angles of the ΔABC and ∠ CAE.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 3
If p = 1 + 21 + 22 + 23 + … + 2n where p is the prime number and n is a natural number. Find all such prime numbers p < 100 and the corresponding natural number n. For each (p, n), find N = p×2n and find the sum of all divisors of N.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 4
The sequence 8, 24, 48, 80, 120, … consists of positive multiples of 8, each of which is one less than a perfect square. Find the 2011th term. Divide it by 2012 and find the quotient.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 5
Each letter of the following words is positive integer. The letters have the same value wherever they occur. The numerical values given for each word is the perfect of the corresponding numbers of the letters appearing in the word. BILL = 35, BLAB = 225, BLANK = 270, SLANG = 2574. Find the value of SINKING. [Example: If P = 12, U = 2, T = 5, then PUT = 120]
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 6
(a) The length of the sides of a triangle are three consecutive odd numbers. The shortest side is 20% of the perimeter. What percentage of the perimeter if the largest side?
(b) The sides of the triangle are three consecutive even numbers and the biggest side is 44(4/9)% of the perimeter. What percentage of the perimeter is the shortest side?
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 7
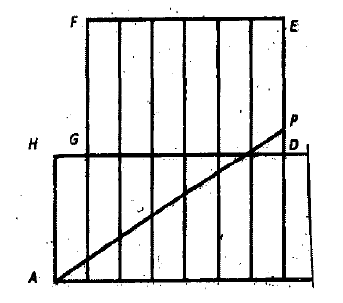
In the figure, all the 14 rectangles are equal in size. The dimensions of each rectangle are 2 units × 5 units. P is a point on ED.
AP divides the octagon ABCDEFGH into two equal parts. Find the length of AP.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 8
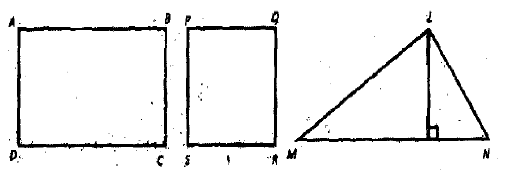
In rectangle ABCD, the length is twice the breadth. In the square, each side is equal to one unit more than the breadth of the rectangle. In the triangle LMN, the altitude is one unit less than the breadth of the rectangle. Area of the rectangle is 18 square units. The sum of the areas of the rectangle and the square is equal to the area of the triangle. What is the base of the triangle and the areas of the square and the triangle?
NMTC Final Stage Previous Year 2012 Question Papers For Class 5 and 6
Instructions:
- Same as previous instructions.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 1
Find the sum (S) of all numbers with 2012 digits and digital sum 2. Find also the digital sum of S.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 2
A number n is called a lonely odd composite number if
(a) n is an odd composite number and
(b) Both (n – 2) and (n + 2) are prime numbers.
{n is odd, hence (n – 2) and (n + 2) are three consecutive odd numbers. Example: n = 105, then (n – 2) = 103 and (n + 2) = 107. Here 105 is an odd composite number 103 and 107 are prime numbers. Therefore, 105 is lonely odd composite number}. Find all ‘lonely odd composite’ number less than 100. Show that these lonely odd composite numbers are multiple of 3.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 3
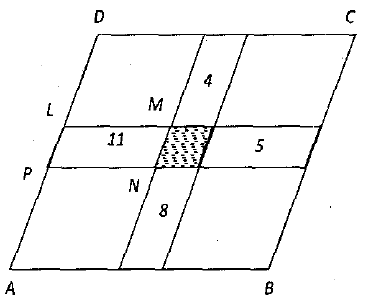
In the adjoining figure, ABCD is a parallelogram of perimeter 21.
It is subdivided into smaller parallelograms by drawing lines parallel to the sides. The number shown are the respective perimeters of the parallelogram in which they are marked. (For example: the perimeter of the parallelogram LMNP is 11). Find the perimeter of the shaded parallelogram.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 4
l and b are two numbers of the form of p/q, where p and q are natural numbers. Further, l and b are greater than 2.
(a) If l = 2b/(b – 2), then prove that b = 2l/(l – 2).
(b) When l takes three values 3, 4 and 8, find the corresponding values of b.
(c) When b takes three values 6, 10 and 12, find the corresponding values of l.
(d) From (b) and (c), we get six values of (l, b). Taking l and b are the length and breadth of a rectangle, find the perimeter and area of the 6 rectangle. What is your inference?
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 5
a, b, c, d are the unit digits of four natural numbers each of which has four digits. The tens digits of these four numbers are the 9 complements of the unit digits. The hundred digits are the 18 complements of the sum of their respective tens and unit digits. The thousand digits are the 27 complement of the sum of their respective hundreds, tens and unit digits. If a + b + c + d = 10, find the sum of these four numbers. {9 complement of a number x is 9 – y, 18 complement of a number y is 18 – x, 27 complement of a number z is 27 – z,}.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 6
A sequence is generated starting with the first term t1, as a four-digits natural number. The second, third and fourth terms (t2, t3 and t4) are got by squaring the sum of the digits of the preceding terms (example: t1 = 9999, then t2 = (9 + 9 + 9 + 9)2 = 362 = 1296, t3 = (1 + 2 + 9 + 6)2 = 182 = 324, t4 = (3 + 2 + 4)2 = 92 = 81). Start with t1 = 2012. Form the sequence and find the sum of the first 2012 terms.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 7
Find the two digit numbers that are divisible by the sum of their digits. Given detailed solutions with logical arguments.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 8
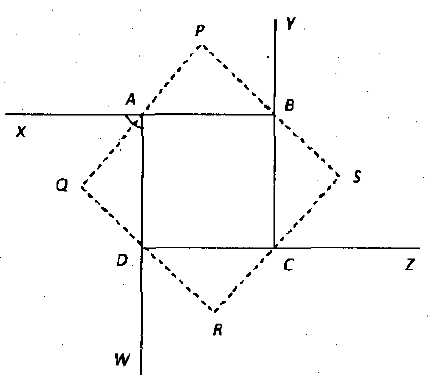
ABCD is a square and the sides are extended as shown in the diagram. The exterior angles are bisected and the bisectors extended to form a quadrilateral PQRS. Prove that PQRS is a square.
NMTC Final Stage Previous Year 2014 Question Papers For Class 5 and 6
Instructions:
- Same as previous instructions.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 1
A three-digits number is divisible by 7 and 8.
(a) How many such number are there?
(b) List out all the numbers.
(c) Spot out the two numbers whose digits um is maximum and minimum.
(d) For how many numbers the digit sum is odd?
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 2
‘a’ is the least number which on being divided by 5, 6, 8, 9 and 12 leaves in each case a remainder 1, but divided by 13 leaves no remainder. ‘b’ is the greatest four-digit number which when divided by 12, 18, 21 and 28 leaves a remainder 3 in each case. Find the value of (b – a).
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 3
L1, L2, L3, L4 are straight lines. L1, L2 intersecting at Q and L3, L4 intersecting at R in the same plane as in the diagram.
The two dotted lines are the bisectors of the respective angles exterior to 86° and 34° and they meet at P. If L1 and L4 make an angle 100°, find the measure of ∠ QPR and what is the angle between the lines L2 and L3? Steps must be written with supporting correct reasons.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 4
Two-digit number 27 is 3 times the sum of the digits. (Example: (2 + 7) × 3 = 27). Find all the two digit numbers each of which is 7 times the sum of its digits and write with proper mathematical steps how you found them.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 5
There is a ten-digit number ‘abcdefghij’ (with a = 1 and all the other digits are equal to either 0 or 1). It has the property that a +c + e + g + i = b + d + f + h + j. how many such 10-digit numbers are there?
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 6
All the natural number from 1 to 12 are written on 6 separate pieces of paper, two numbers on each piece. The six sum of the numbers on these six pieces are respectively 4, 6, 13, 14, 20 and 21. Find out the integer in each pair written on each piece of paper and explain how you found them.
NMTC Final Stage Previous Year 2015 Question Papers For Class 5 and 6
Instructions:
- Same as previous instructions.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 1
A unit fraction is one of the form 1/a, where a is a natural number and not equal to 1. Any proper fraction can be written as the sum of two or more unit fractions. {Example: 1/2 = 1/3 + 1/6, 5/6 = 1/2 + 1/3, 1/24 = 1/54 + 1/72 + 1/108}. In the case of 1/2, the factors of 2 are 1 and 2 only. 1/2 = (1 + 2)/(2(1 + 2)) = 1/2(1 + 2) + 2/2(1 + 2) = 1/6 + 1/3.
Express 1/15 as the sum of two different unit fraction in 4 different ways.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 2
(a) The number 11284 and 7655 when divided by a certain three-digits number leave the same remainder. Find the number and the remainder.
(b) What is the least number to be subtracted from 1936 so that when divided by 9, 10 and 15 it will leave the same remainder in each case?
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 3
A, M, T, I represent different non-zero digits. It is given that A + M + T + I = 11, A + M + T = 10, A + M = 1, Further in the following addition only one digit is given. Fill up the stars writing proper reasons.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 4
ABC is a three-digit number in which the digit A is greater than the digit B and C. If the difference between ABC and CBA is 297 and the difference between ABC and BAC is 450, find all possible three digit numbers ABC and their sum also.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 5
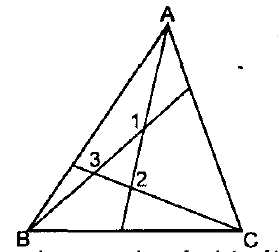
Take a triangle. Three straight lines are drawn through the vertices of the triangle as shown. The maximum number of points of intersection is 3. Draw two lines through each vertex of a triangle to meet the opposite sides. What is the maximum number of points of intersection?
Find again drawing the maximum number of points of intersection when three lines are drawn through each vertex. Without drawing can you guess the maximum points of intersection for four lines.
NMTC Final Stage Previous Year 2016 Question Papers For Class 5 and 6
Instructions:
- Same as Previous Instructions.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 1
(a)
I. In how many ways can two identical balls be placed in 3 different boxes so that exactly one box is empty?
II. In how many ways can three identical balls be placed in 2 different boxes so that exactly one box is empty?
III. In how many ways can four identical balls be placed in 2 different boxes so that exactly one box is empty?
(b)
A positive integer n has five digits. N is the six-digit number obtained by adjoining 2 as the leftmost digit of n. M is the six-digit number by adjoining 2 at right most digit of n. If M = 3N, find all the values of n.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 2
(a) 1800 is expressed 2a × 3b × 5c and 1620 is expressed 2d × 3e × 5f, where a, b, c, d, e, f are positive integers. Find the remainder when 2016 is divided by a + b + c + d + e + f.
(b) Three persons A, B, C whose salaries together amount Rs. 14400 spend 80%, 85% and 75% of their respective salaries. If their saving are as 8 : 9 : 20, find their individual salaries.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 3
Completely simply the fraction.
By x/y of a/b, we mean x/y × a/b.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 4
p, q, r are prime numbers and r is the single digit number. If pq + r = 1993, find p + q + r.
NMTC Final Stage Previous Year Question For Class 5 and 6: Ques No 5
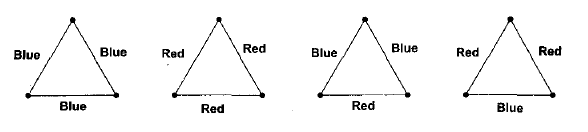
(a) If we take sticks of the same colour and same length, we can make one triangle using them. If we have of same length but two different colours, say blue and red, we can make four triangles as shown below.
How many triangles can be found using sticks of same length but three different colors, say Red, Blue and Green?
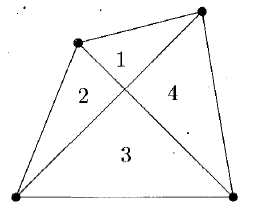
(b) The diagonals of a quadrilateral divide the quadrilateral into four regions. Draw a pentagon and find the maximum number of regions that can be obtained by drawing line segments connecting any two vertices.