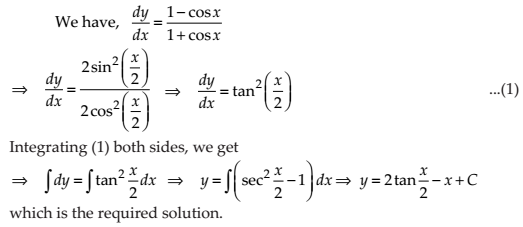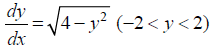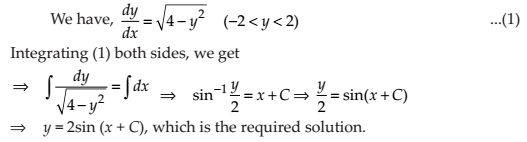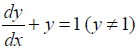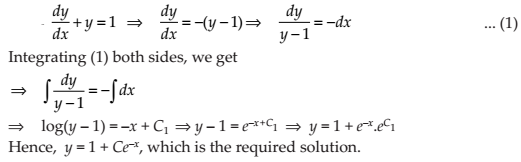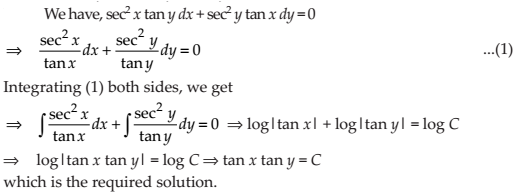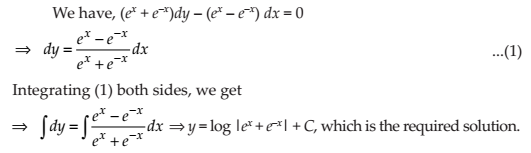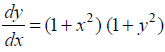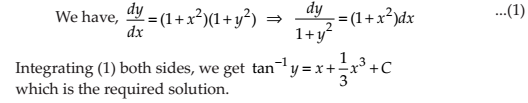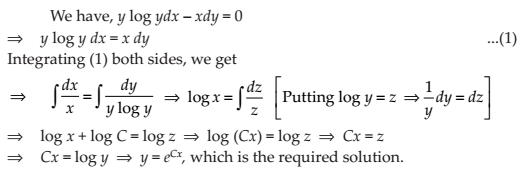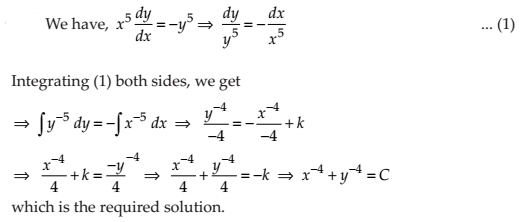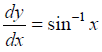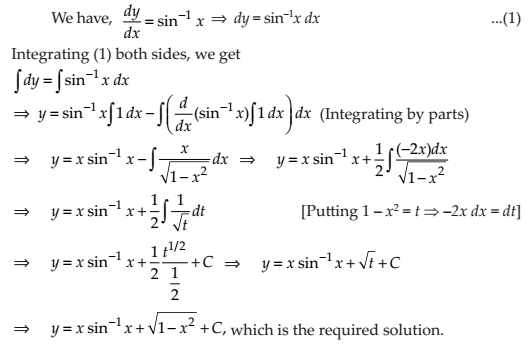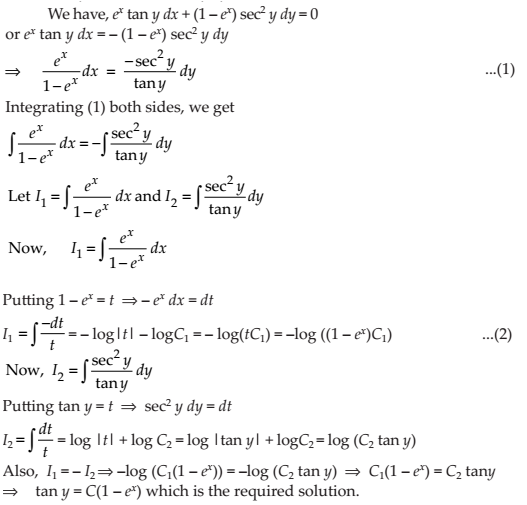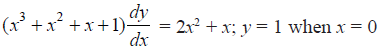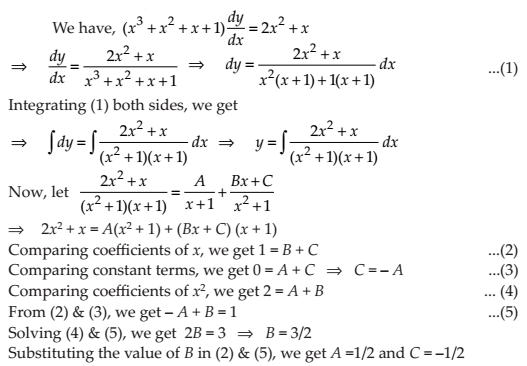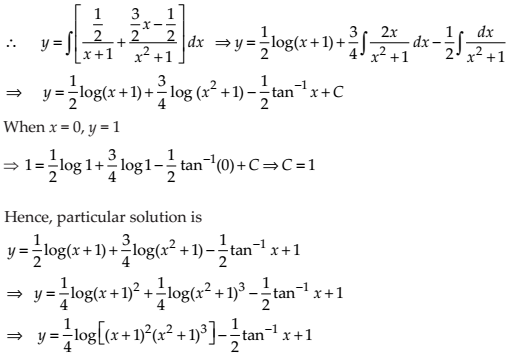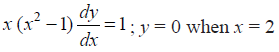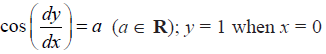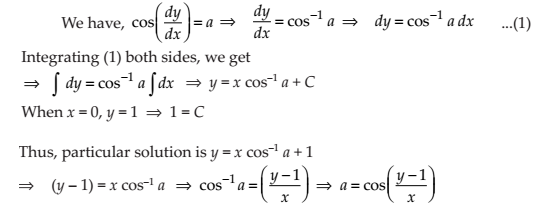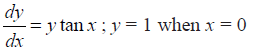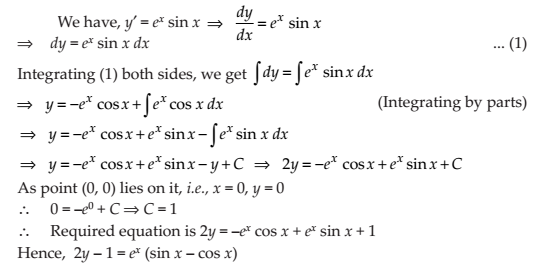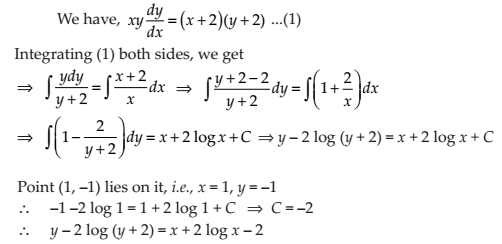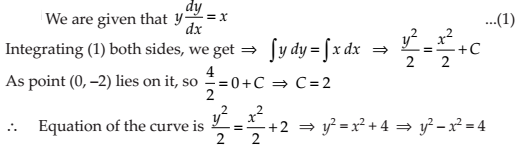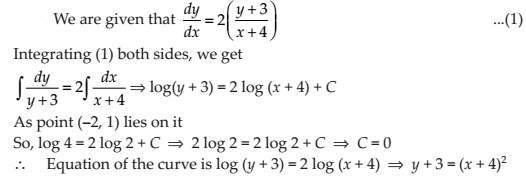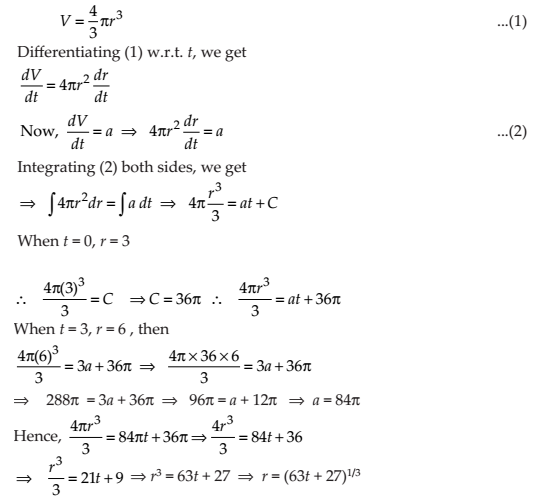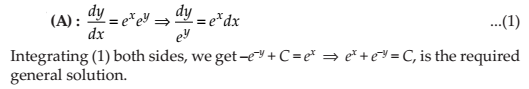Hi Students, Welcome to Amans Maths Blogs (AMB). In this post, you will get the NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4.
The PDF books of NCERT Solutions for Class 12 are the first step towards the learning and understanding the each sections of Maths, Physics, Chemistry, Biology as it all help in engineering medical entrance exams. To solve it, you just need to click on download links of NCERT solutions for class 12.
CBSE Class 12th is an important school class in your life as you take some serious decision about your career. And out of all subjects, Maths is an important and core subjects. So CBSE NCERT Solutions for Class 12th Maths is major role in your exam preparation as it has detailed chapter wise solutions for all exercise. This NCERT Solutions can be downloaded in PDF file. The downloading link is given at last.
As we know that all the schools affiliated from CBSE follow the NCERT books for all subjects. You can check the CBSE NCERT Syllabus. Thus, NCERT Solutions helps the students to solve the exercise questions as given in NCERT Books.
NCERT Solutions for class 12 is highly recommended by the experienced teacher for students who are going to appear in CBSE Class 12 and JEE Mains and Advanced and NEET level exams. Here You will get NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4 of all questions given in NCERT textbooks of class 12 in details with step by step process.
NCERT Solutions for Class 12 Maths are not only the solutions of Maths exercise but it builds your foundation of other important subjects. Getting knowledge of depth concept of CBSE Class 12th Maths like Algebra, Calculus, Trigonometry, Coordinate Geometry help you to understand the concept of Physics and Physical Chemistry.
NCERT Solutions for Class 12 Maths Differential Equations
For each of the differential equations in Exercises 1 to 10, find the general solution:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 1.
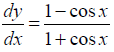
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 2.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 3.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 4.
sec2 x tan y dx + sec2 y tan x dy = 0
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 5.
(ex + e–x) dy – (ex – e–x) dx = 0
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 6.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 7.
y log y dx – x dy = 0
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 8.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 9.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 10.
ex tan y dx + (1 – ex) sec2 y dy = 0
NCERT Solutions:
For each of the differential equations in Exercises 11 to 14, find a particular solution satisfying the given condition:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 11.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 12.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 13.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 14.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 15.
Find the equation of a curve passing through the point (0, 0) and whose differential equation is y′ = ex sin x.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 16.
For the differential equation xy(dy/dx) = (x + 2)(y + 2), find the solution curve passing through the point (1, –1).
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 17.
Find the equation of a curve passing through the point (0, –2) given that at any point (x, y) on the curve, the product of the slope of its tangent and y coordinate of the point is equal to the x coordinate of the point.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 18.
At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (– 4, –3). Find the equation of the curve given that it passes through (–2, 1).
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 19.
The volume of spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of balloon after t seconds.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 20.
In a bank, principal increases continuously at the rate of r% per year. Find the value of r if Rs 100 double itself in 10 years (loge2 = 0.6931).
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 21.
In a bank, principal increases continuously at the rate of 5% per year. An amount of Rs 1000 is deposited with this bank, how much will it worth after 10 years (e0.5 = 1.648).
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 22.
In a culture, the bacteria count is 1,00,000. The number is increased by 10% in 2 hours. In how many hours will the count reach 2,00,000, if the rate of growth of bacteria is proportional to the number present?
NCERT Solutions:
NCERT Solutions for Class 12 Maths Differential Equations Exercise 9.4: Ques No 23.
The general solution of the differential equation dy/dx = ex+y is
(A) ex + e–y = C
(B) ex + ey = C
(C) e–x + ey = C
(D) e–x + e–y = C
NCERT Solutions: