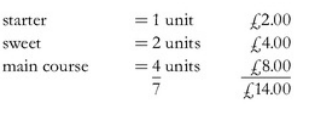Hi students, Welcome to Amans Maths Blogs (AMBIPi). Are you looking for Math Puzzles for Adult Questions 41 to 60 with Answer AMBIPi for brain exercise? In this article, you will get challenging math riddles with answers. Solving these tricky math puzzles are brain exercise and you can do solve these in anytime as you wish.
Hard Math Riddles 41: On their way to Chicago for a conference of authors and journalists, six writers meet in a railroad club car.
Three of them sit on one side facing the other three.
Each of the six has his specialty.
One writes short stories, one is a historian, another one writes humorous books, still another writes novels, the fifth is a playwright and the last a poet.
Their names are Blank, Bird, Grelly, George, Pinder and Winch.
Each of them has brought one of his books and given it to one of his colleagues, so that each of the six is deep in a book which one of the other five has written.
Blank reads a collection of short stories.
Grelly reads the book written by the colleague sitting just opposite him.
Bird sits between the author of short stories and the humorist.
The short-story writer sits opposite the historian.
George reads a play. Bird is the brother-in-law of the novelist.
Pinder sits next to the playright. Blank sits in a corner and is not interested in history.
George sits opposite the novelist.
Pinder reads a humorous book.
Winch never reads poems.
Using these facts, find each of the six authors’ specialties.
Show/Hide Answer Key
Answer:
Explanation: Grelly is a playwright, Pinder is a historian, George writes humorous books, Bird is a poet, Winch writes short stories, and Blank writes novels.
Hard Math Puzzles 42: Sums are not set as a test on Erasmus.
Palindromes have always fascinated Hannah. Her boyfriend’s name is Bob, she lives alone at her cottage in the country named Lonely Tylenol, and drives her beloved car, which is a Toyota.
A few days ago Hannah was driving along the motorway when she glanced at the mileage indicator and happened to notice that it displayed a palindromic number; 13931.
Hannah continued driving and two hours later again glanced at the odometer, and to her surprise it again displayed another palindrome.
What average speed was Hannah travelling, assuming her average speed was less than 70 mph?
Show/Hide Answer Key
Answer: 55 mph
Explanation: The next palindromic number after 13931 is 14041. Hannah must have, therefore, travelled 110 miles. As she travelled for 2 hours, her average speed must have been 55 mph
Math Riddles Hard 43: There are not many mountains in the world which have not yet been explored and climbed from all sides.
But recently an American expedition found some heretofore unknown mountain ranges that look as if they might pose some new problems.
Let’s call one of the newly discovered mountains Mt. Antarctic and let us imagine that during the next Antarctic expedition a party of explorers decides to walk around the mountain at its base.
The complete circuit is 100 miles and, of course, it leads through very cold, inhospitable country. Naturally, in the Antarctic the party has to rely exclusively on the provisions it can take along.
The men cannot carry more than two days’ rations at a time and each day they have to consume one of these during the march. Each ration is packed as two half-rations. No doubt, it will be necessary to establish depots on the 100-mile circular route, to which the men will have to carry rations from the camp.
The greatest distance the party can walk in a day is 20 miles.
The questions is, what is the shortest time needed for the party to make the circuit around Mt. Antarctic?
A rather primitive solution would consist of dumping a great number of rations at a point 10 miles from the camp, then carrying half of them to a point 20 miles from the camp, and so on, and so forth, until two daily rations have been dumped at a point 60 miles from camp, from which point the party could reach the camp in two days.
With this procedure the party would need about 130 days to complete the circuit. But the number of day’s journeys needed for the expedition may be cut considerably by establishing depots around the mountain in both directions from the camp.
However, this solution, too, is by no means the most efficient. The job can be done in a much shorter period, without using any tricks such as fasting or eating the day’s ration before starting at dawn to be able to carry two daily rations to the next depot.
Show/Hide Answer Key
Answer:
Explanation: The trip around the mountain need not take longer than 18 days, if division of the day’s rations into half rations is permitted. The party itself is not divided. To dump one and one half rations at 5 miles and return to camp requires half a day. One day is needed for depositing one and one-half rations at 10 miles. To supplement that day’s provisions, half a day’s ration may be taken from the food stored at 5 miles. Two days are required to get one ration to the 20-mile point. Now we have stores of one-half ration at 5 miles and of one ration each at 10 and 20 miles. Within three more days, one-half ration may be dumped at 30 miles. That adds up to 61 days. The same number of days is required for dumping half-ration stores at the other end of the circuit, at 90, 80 and 70 miles. Add to these 13 days five more for
the final hike around the mountain, and you get 18 days, all told.
Hard Math Brain Teasers 44: The average of three numbers is 17. The average of two of these numbers is 25.What is the third number?
Show/Hide Answer Key
Answer: 26
Explanation:
Three numbers 17 × 3 = 51
Two numbers 12:5 × 2 = 25
The third number is 51 – 25 = 26.
Math Riddles Hard 45: Five horses, Condor, Fedor, Tornado, Star and Riotinto, are entered in a race.
Their post position numbers-though not in the same order-are 1 to 5.
The jockeys riding these horses have the following names: Reynolds, Shipley, Finley, Semler and Scranton.
The odds are whole numbers between 1 and 6 inclusive and are different for each horse.
This is the outcome of the race: Reynolds is winner and Finley is last.
The favorite, for whom, of course, the lowest odds would have been paid, finishes third.
Tornado’s position at the finish is higher by one than his post position number.
Star’s post position number is higher by one than his rank at the finish.
Condor’s post position number is the same as Fedor’s finishing position.
Only Riotinto has the same post position and finishing rank.
The outsider with the odds 6 to 1 finishes fourth.
The horse that comes in second is the only horse whose name starts with the same letter as his jockey’s name.
The odds on Shipley’s horse are equal to his post position number; those on Fedor exceed his rank at the finish by one; those on Condor are equal to his position at the finish and exceed by one the position of Semler’s horse at the finish.
What are the names, jockeys’ names, post position numbers and odds of these five race horses and in what order do they come in at the finish?
Show/Hide Answer Key
Answer:

Explanation: Since Reynolds rides the winning horse and Finley’s horse is last, two combinations – names of horses and jockeys beginning
with the same letter-are out of the question for entry number 2. We can eliminate Reynolds-Riotinto and Finley-Fedor. Only Star can be second, and the name of his jockey may be Shipley, Scranton or Semler. Condor, whose odds equal his position at the finish, cannot be the winner, nor can he have come in third, coincident with the lowest odds, 1 to 1. Neither can he have come in fourth, coincident with the odds 6 to 1. Therefore, Condor is fifth and his odds are 5 to 1. Hence Semler’s horse is fourth. Riotinto, whose jockey is not Reynolds, has the same post position and rank at the finish. They cannot be 3 and thus must be 4. Tornado’s position at the finish is one higher than his post position number. Thus, it is out of the question that Tornado could have been the winning horse. Therefore, his post position number must have been 2 and he must have come in third at the finish. Because post position and finishing rank are in no case identical, with the
exception of Riotinto, the post position number of Reynolds’ horse is 5 and that of Finley’s horse, Condor, 1. This leaves Reynolds’ horse, Fedor, as the winner of the race, with the odds 2 to 1. The odds on Shipley’s horse are the same as his post position number, which means that the odds on his horse, Star, are 3 to 1. Thus, Scranton rides Tornado.
Hard Brain Teasers 46: You have 62 cubic blocks. What is the minimum number that needs to be taken away in order to construct a solid cube with none left over?
Show/Hide Answer Key
Answer: 35
Explanation: The next cube number below 64 is 27 (3 × 3 × 3). In order to construct a 3 × 3 × 3 solid cube, therefore, with none left over, 62 – 27 = 35 blocks need to be taken away.
Hard Math Riddles for Adults 47: Some years ago, on the last day of July, a very fashionable Fifth Avenue store opened a new department for expensive dresses.
The five sales girls hired for the new department were asked to contribute their share to the show by wearing, every succeeding day for a month after the opening, a different colored dress, as far as their own wardrobes and budgets permitted.
As a merchandising experiment the store was kept open every day, Sundays included.
Now this is the way the girls cooperated: None of them owned more than ten dresses, while one had only one good dress which she wore every day.
The others rotated their wardrobes so that they always wore their dresses in the same order (for instance, yellow, red, blue, yellow, red, blue, yellow, etc.).
None of the girls owned two dresses of the same color and each had a different number of dresses.
One of the store’s best customers who dropped in every day all through August and who, of course, didn’t miss the slightest detail in the sales girls’ wardrobe, kept track of the daily changes and made the following observations:
On August 1st, Emily wore a grey dress, Bertha and Celia red ones, Dorothy a green one and Elsa a yellow one.
On August 11th, two of the girls were in red, one in lilac, one in grey and one in white.
On August 19th, Dorothy had a green dress, Elsa a yellow one and the three other girls red ones.
Dorothy had on a yellow dress on August 22nd and a white one on August 23rd.
On the last day of the month all five sales girls wore the same dresses as on the first day of August.
These are all the mental notes the faithful customer and observer took.
However, when some time later, someone asked her whether she could find out which of the girls had worn a lilac colored dress on August 11th, she was able to answer that question with the aid of a pencil, a piece of paper and her fragmentary recollections.
Try whether you can do the same!
Show/Hide Answer Key
Answer:
Explanation: We can make the following statements and conclusions:
(I) Bertha, Celia, Dorothy and Elsa wore the same dresses on the 1st, the 19th and the 31st, that is with intervals of 18 and 12 days. The number of dresses they own, therefore, must be a common divisor of 12 and 18- that is, any of the numbers 1, 2, 3 and 6.
(2) Dorothy has six dresses. She cannot own only one or two because we have already been told that she wore three different colors. On the other hand, she cannot have only the three dresses listed because, in that case, on the 22nd she would have worn the same green dress she wore on the 19th. On the 22nd, however, she wore a yellow one.
(3) Emily wore her grey dress on the 1st and the 31st of the month. Consequently, the number of her dresses must be a divisor of 30 – that is, any of the whole numbers 1, 2, 3, 5 and 10. According to (1), 1, 2, 3 and 6 are the numbers pertaining to the other four girls. Therefore, Emily owns either five or ten dresses and consequently, in either of these cases, she had on a grey dress on the 11th.
(4) None of the five girls wore a yellow dress on the 11th; therefore, we may be sure that Elsa did not wear a yellow dress on this day and, consequently, owns more than one dress. That means that she owns either two or three dresses. If she had only two, she would have worn a yellow one on the 11th, just as she did on the first of the month. However, that is impossible since on the 11th nobody wore a yellow dress. So Elsa owns three dresses. Bertha and Celia own one or two dresses, respectively, which means that on the 11th both must
have made their appearance in red, one of them because she owns but one dress, the other, who owns two, because on the 11th she
must have worn the same dress she wore on the 1st.
(5) Dorothy had on a green dress on the 31st and eight days before, on the 23rd, she wore a white dress. That means that she must also have worn a white dress eight days previous to the 19th, because on the 19th she also wore a green dress. So on the 11th she could
not have worn a lilac-colored dress either. Consequently, on that crucial day, only Elsa could have worn the lilac-colored dress, since
of the five dresses worn that day the four others were worn by Emily, Bertha, Celia and Dorothy.
Hard Maths Puzzles 48: I bought two watches, an expensive one and a cheap one. The expensive one cost £200 more than the cheap one and altogether I spent £220 for both. How much did I pay for the cheap watch?
Show/Hide Answer Key
Answer: £10.00.
Explanation: The temptation is to say £20.00 for the cheap watch. This is not correct as £200.00 and £20.00 only represents a difference of £180.00, not £200.00. The answer is that the cheap watch cost £10.00. The difference between £10 and £210 is, therefore, £200 as stipulated in the question.
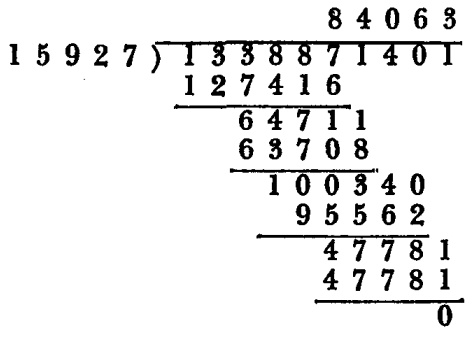
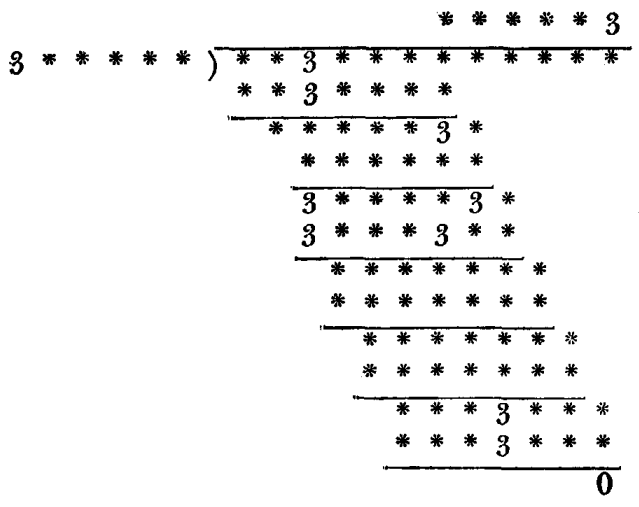
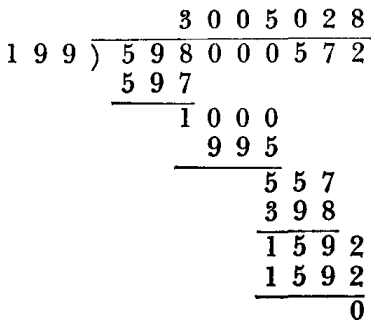
Math Puzzles Hard 49: This division has two peculiarities. First, all ones that occurs in the course of the operation are still legible, and second, all whole numbers from 0 to 9, inclusive, occur once in the ten digits that are included in divisor and quotient, together.
Show/Hide Answer Key
Answer:
Explanation:
Hard Math Riddles for School Students 50: If 6 apples and 4 bananas cost 78 pence and 7 apples and 9 bananas cost 130 pence what is the cost of one apple and what is the cost of one banana?
Show/Hide Answer Key
Answer: Apple = 7 pence and banana = 9 pence.
Explanation: Multiply the top line by 7 and the bottom line by 6. Then 42 apples and 28 bananas cost 546 pence 42 apples and 54 bananas cost 780 pence subtracting, therefore, 26 (54 – 28) bananas cost 234 (780 – 546) pence (or 9 pence each) as six apples and four bananas cost 78 pence, then (6 × apples) plus (4 × 9) = 78 pence.
So, six apples cost 42 pence (78 – 36), and one apple costs 7 pence.
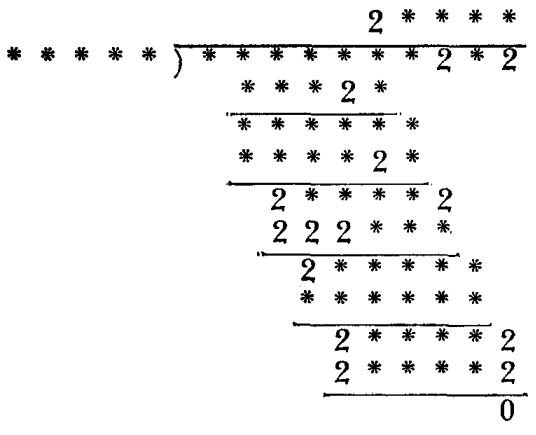
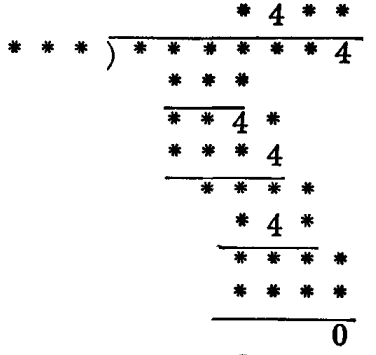
High School Math Puzzles 51: In this puzzle, also, all twos which occur in the operation have remained legible, and the divisor and quotient together contain all the one-digit figures from 0 to 9 inclusive.
Show/Hide Answer Key
Answer:
Explanation:
High School Math Brain Teasers 52: The cost of a three-course lunch was £14.00. The main course cost twice as much as the sweet, and the sweet cost twice as much as the starter. How much did the main course cost?
Show/Hide Answer Key
Answer: £8.00.
Explanation: The cost per unit = £2:00(14/7)
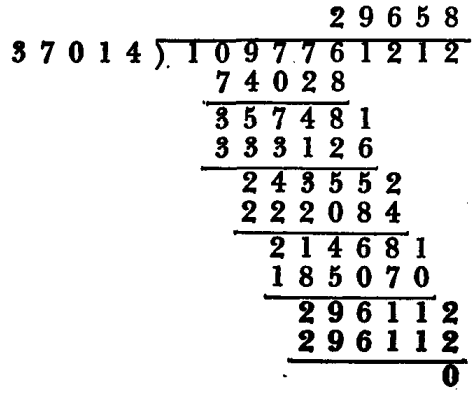
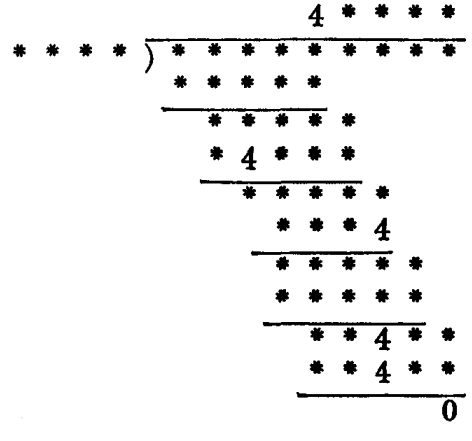
High School Math Puzzles 53: In this problem all the threes that occur have remained legible. Moreover, the quotient contains all the numbers in the divisor, but they occur in reverse order.
Show/Hide Answer Key
Answer:
Explanation:
High School Math Reasoning 54: My watch was correct at midnight, after which it began to lose 12 minutes per hour, until 7 hours ago it stopped completely. It now shows the time as 3.12. What is now the correct time?
Show/Hide Answer Key
Answer: 11 am
Explanation: If the watch loses 12 minutes per hour it takes 4 hours to lose 48 minutes; i.e., when the correct time is 4 am the watch will show 3.12. As this is the time the watch is now showing it must have stopped at 4 am, therefore the time is now 4 am plus 7 hours = 11 am.
plus 7 hours = 11 am.
Best Math Puzzles for Adults 55: The following skeleton of a division represents a comparatively easy “faded document.” But, in contrast to the previous problems, not all the fours that occur have been “preserved.”
Show/Hide Answer Key
Answer: Twice.
Explanation:
Math Brain Teasers for Adults 56: A photograph measuring 7.5 cm by 6.5 cm is to be enlarged. If the enlargement of the longest side is 18 cm, what is the length of the smaller side?
Show/Hide Answer Key
Answer: 15.6 cm.
Explanation: (18 / 7:5) × 6:5.
Math Riddles for Adults 57: Here, all the fours that occur remain readable and, this time, only all the integers from 1 to 9 inclusive occur in the nine figures of the divisor and quotient.
Show/Hide Answer Key
Answer:
Explanation:
Math Puzzles for Adults 58: A statue is being carved by a sculptor. The original piece of marble weighs 140 lb. On the first week 35% is cut away. On the second week the sculptor chips off 26lb and on the third week he chips off two-fifths of the remainder, which completes the statue. What is the weight of the final statue?
Show/Hide Answer Key
Answer: 39lb
Explanation:
140 less 35% = 91
91 – 26 = 65
65 less (26) = 39.
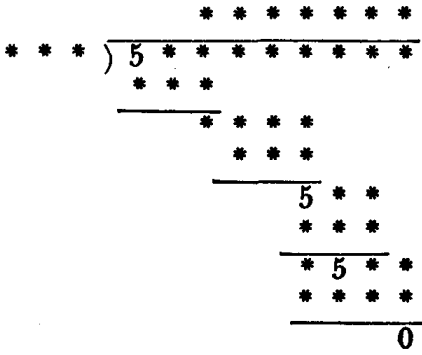
Math Puzzles for Adults 59: The three fives remaining in the following skeleton are sufficient to reconstruct the entire division. However, not every five which occurs in the problem shows up.
Show/Hide Answer Key
Answer:
Explanation: This is only one of several possible solutions.
Math Puzzles for Adults 60: The ages of five family members total 65 between them.
Alice and Bill total 32 between them Bill and Clara total 33 between them Clara and Donald total 28 between them Donald and Elsie total 7 between them. How old is each family member?
Show/Hide Answer Key
Answer: Alice 25, Bill 7, Clara 26, Donald 2, Elsie 5.
Explanation: