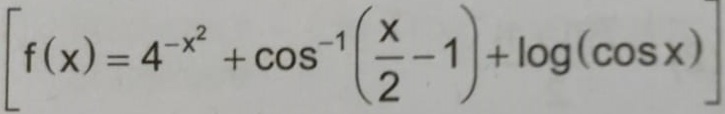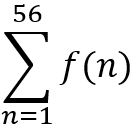Welcome to AMBiPi (Read as: एम्बीपाई) (Amans Maths Blogs). JEE Mains and JEE Advanced exams are the engineering entrance exams for taking admission in IITs, NITs and other engineering colleges. In this article, you will get JEE Main Math Previous Year Papers Sets Relations Functions Questions Answer Keys Solutions.
JEE Mains Mathematics Sets Relations and Functions Questions Bank
Enter Questions No: 1
The domain of sin-1[log3 (x/3)] is
[2002]
Option A: [1, 9]
Option B: [-1, 9]
Option C: [-9, 1]
Option D: [-9, -1]
Show/Hide Answer Key
Option A: [1, 9]
Enter Questions No: 1
If f(x + y) = f(x) ∙ f(y) for all x and y and f(5) = 2, f'(0) = 3, then find f'(5).
[2002]
Option A: 0
Option B: 1
Option C: 6
Option D: 2
Show/Hide Answer Key
Option C: 6
Enter Questions No: 1
Which one is NOT periodic?
[2002]
Option A: |sin 3x| + sin2x
Option B: cos √x + cos2x
Option C: cos 4x + tan2x
Option D: cos 2x + sin x
Show/Hide Answer Key
Option B: cos √x + cos2x
Enter Questions No: 1
The period of sin2θ is
[2002]
Option A: π2
Option B: π
Option C: π3
Option D: π/2
Show/Hide Answer Key
Option B: π
Enter Questions No: 1
The function f(x) = log(x + √(x2 + 1))
[2003]
Option A: An Even Function
Option B: An Odd Function
Option C: A Periodic Function
Option D: Neither an Even nor an Odd Function
Show/Hide Answer Key
Option B: An Odd Function
Enter Questions No: 1
Domain of definition of the function f(x) = 3 / (4 – x2) + log10(x3 – x) is
[2003]
Option A: (1, 2)
Option B: (-1, 0) ∪ (1, 2)
Option C: (1, 2) ∪ (2, ∞)
Option D: (-1, 0) ∪ (1, 2) ∪ (2, ∞)
Show/Hide Answer Key
Option D: (-1, 0) ∪ (1, 2) ∪ (2, ∞)
Enter Questions No: 1
If f : R → R satisfies f(x + y) = f(x) + f(y), for all x, y ∊ R and f(1) = 7, then
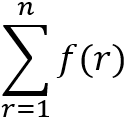
[2003]
Option A: 7n / 2
Option B: 7(n + 1) / 2
Option C: 7n(n + 1)
Option D: 7n(n + 1) / 2
Show/Hide Answer Key
Option D: 7n(n + 1) / 2
Enter Questions No: 1
A function f from the set of natural numbers to integers defined by
is
[2003]
Option A: One-One but Not Onto
Option B: Onto but Not One-One
Option C: One-One and Onto Both
Option D: Neither One-One Nor Onto
Show/Hide Answer Key
Option C: One-One and Onto Both
Enter Questions No: 1
Let R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1)} be a relation on the set A = {1, 2, 3, 4}. The relation R is
[2004]
Option A: a function
Option B: reflexive
Option C: not symmetric
Option D: transitive
Show/Hide Answer Key
Option C: not symmetric
Enter Questions No: 1
The domain of the function f(x) = sin-1(x – 3) / √(9 – x2) is
[2004]
Option A: [2, 3]
Option B: [2, 3)
Option C: [1, 2]
Option D: [1, 2)
Show/Hide Answer Key
Option C: One-One and Onto Both
Enter Questions No: 1
The graph of the function y = f(x) is symmetrical about the line x = 2, then
[2004]
Option A: f(x + 2) = f(x – 2)
Option B: f(2 + x) = f(2 – x)
Option C: f(x) = f(-x)
Option D: f(x) = -f(-x)
Show/Hide Answer Key
Option B: f(2 + x) = f(2 – x)
Enter Questions No: 1
If f : R → S, defined by f(x) = sin x – √3cos x + 1 is onto, then the interval of S is
[2004]
Option A: [0, 3]
Option B: [-1, 1]
Option C: [0, 1]
Option D: [-1, 3]
Show/Hide Answer Key
Option D: [-1, 3]
Enter Questions No: 1
The range of the function f(x) = 7-xPx-3 is
[2004]
Option A: {1, 2, 3}
Option B: {1, 2, 3, 4, 5}
Option C: {1, 2, 3, 4}
Option D: {1, 2, 3, 4, 5, 6}
Show/Hide Answer Key
Option A: {1, 2, 3}
Enter Questions No: 1
Let R = {(3, 3), (6, 6), (9,9), (12, 12), (6, 12), (3, 9), (3, 12), (3, 6)} be a relation on the set A = {3, 6, 9, 12} be a relation on the set A = {3, 6, 9, 12}. The relation is
[2005]
Option A: reflexive and transitive only
Option B: reflexive only
Option C: an equivalence relation
Option D: reflexive and symmetric only
Show/Hide Answer Key
Option A: reflexive and transitive only
Enter Questions No: 1
Let f : (-1, 1) → B, be a function defined by f(x) = tan-1(2x / (1 – x2)), then the function f is both one-one and onto when B is the interval
[2005]
Option A: (0, π/2)
Option B: [0, π/2)
Option C: [-π/2, π/2]
Option D: (-π/2, π/2)
Show/Hide Answer Key
Option D: (-π/2, π/2)
Enter Questions No: 1
A real valued function f(x) satisfies the functional equation f(x – y) = f(x)f(y) – f(a – x)f(a + y) where a is a given constant and f(0) = 0, f(2a – x) is equal to
[2005]
Option A: -f(x)
Option B: f(x)
Option C: f(a) + f(a – x)
Option D: f(-x)
Show/Hide Answer Key
Option A: -f(x)
Enter Questions No: 1
Let W denote the words in English dictionary. Define the relation R by R = {(x, y) ∈ W × W | the words x and y have at least one letter in common}. Then, R is
[2006]
Option A: not reflexive, symmetric and transitive
Option B: reflexive, symmetric and not transitive
Option C: reflexive, symmetric and transitive
Option D: reflexive, not symmetric and transitive
Show/Hide Answer Key
Option B: reflexive, symmetric and not transitive
Enter Questions No: 1
The largest interval lying in (-π/2, π/2) for which the function
is defined, is
[2007]
Option A: [0, π]
Option B: (-π/2, π/2)
Option C: [-π/4, π/2)
Option D: [0, π/2)
Show/Hide Answer Key
Option D: [0, π/2)
Enter Questions No: 1
Let R be the real line. Consider the following subsets of the plane R × R. S = {(x, y) : y = x + 1 and 0 < x < 2}, T = {(x, y) : x-y is an integer}. Which one of the following is true?
[2008]
Option A: neither S nor T is an equivalence relation on R
Option B: both S and T are equivalence relations on R
Option C: S is an equivalence relation on R but T is not
Option D: T is an equivalence relation on R but S is not
Show/Hide Answer Key
Option D: T is an equivalence relation on R but S is not
Enter Questions No: 1
Let f : N → Y be a function defined as f(x) = 4x + 3, where Y = {y ∈ N : y = 4x + 3 for some x ∈ N}. If f is invertible function, then its inverse function is
[2008]
Option A: g(y) = (3y + 4) / 3
Option B: g(y) = 4 + (y + 3) / 4
Option C: g(y) = (y + 3) / 4
Option D: g(y) = log | sin (x – π / 4) | + c
Show/Hide Answer Key
Option D: g(y) = log | sin (x – π / 4) | + c
Enter Questions No: 1
If A, B and C are three sets such that A ∩ B = A ∩ C and A ∪ B = A ∪ C, then
[2009]
Option A: A = B
Option B: A = C
Option C: B = C
Option D: A ∩ B = φ
Show/Hide Answer Key
Option C: B = C
Enter Questions No: 1
For real x, let f(x) = x3 + 5x + 1, then
[2009]
Option A: f is one-one but not onto R
Option B: f is onto R but not one-one
Option C: f is one-one and onto R
Option D: f is neither one-one nor onto R
Show/Hide Answer Key
Option C: f is one-one and onto R
Enter Questions No: 1
Consider the following relations:
R = {(x, y) | x, y are real numbers and x = wy for some rational number w}
S = {(m/n, p/q) | m,n, p and q are integers such that n, q ≠ 0 and qm = pn}. Then,
[2010]
Option A: neither R nor S is an equivalence relation
Option B: S is an equivalence relation but R is not an equivalence relation
Option C: R and S both are equivalence relations
Option D: R is an equivalence relation but S is not an equivalence relation
Show/Hide Answer Key
Option B: S is an equivalence relation but R is not an equivalence relation
Enter Questions No: 1
The domain of the function f(x) = 1 / √(|x| – x) is
[2011]
Option A: (0, ∞)
Option B: (-∞, 0)
Option C: (-∞, ∞) – {0}
Option D: (-∞, ∞)
Show/Hide Answer Key
Option B: (-∞, 0)
Enter Questions No: 1
The range of the function f(x) = x / (1 + |x|), x ∈ R, is
[2012]
Option A: R
Option B: (-1, 1)
Option C: R – {0}
Option D: [-1, 1]
Show/Hide Answer Key
Option B: (-1, 1)
Enter Questions No: 1
Let A and B be two sets containing two elements and four elements respectively. The number of subsets of A × B having three or more elements is
[2013]
Option A: 220
Option B: 219
Option C: 211
Option D: 256
Show/Hide Answer Key
Option B: 219
Enter Questions No: 1
If X = {4n – 3n – 1 : n ∈ N} and Y = {9(n – 1) : n ∈ N}, where N is the set of natural numbers, then X ∪ Y is equal to
[2014]
Option A: N
Option B: Y – X
Option C: X
Option D: Y
Show/Hide Answer Key
Option D: Y
Enter Questions No: 1
If g is the inverse of a function f and f ‘(x) = 1 / (1 + x5), then g ‘(x) is equal to
[2014]
Option A: 1 + x5
Option B: 5x4
Option C: 1 / [1 + {g(x)}5]
Option D: 1 + {g(x)}5
Show/Hide Answer Key
Option D: 1 + {g(x)}5
Enter Questions No: 1
If a ∈ R and the equation -3(x – [x])2 + 2(x – [x]) + a2 = 0 (where [x] denotes the greatest integer ≤ x) has no integral solution, then all possible values of a lie in the interval
[2014]
Option A: (-1, 0) ∪ (0, 1)
Option B: (1, 2)
Option C: (-2, -1)
Option D: (-∞, -2) ∪ (2, ∞)
Show/Hide Answer Key
Option A: (-1, 0) ∪ (0, 1)
Enter Questions No: 1
Let f(n) = [1/3 + 3n/100]n, where [n] denotes the greatest integer less than or equal to n. Then
is equal to
[2014]
Option A: 56
Option B: 689
Option C: 1287
Option D: 1399
Show/Hide Answer Key
Option D: 1399
Enter Questions No: 1
Let f be an odd function defined on the set of real numbers such that for x ≥ 0, f(x) = 3 sin x + 4 cos x. Then, f(x) at x = -11π/6 is equal to
[2014]
Option A: 3/2 + 2√3
Option B: –3/2 + 2√3
Option C: 3/2 – 2√3
Option D: –3/2 – 2√3
Show/Hide Answer Key
Option C: 3/2 – 2√3
Enter Questions No: 1
Let A and B be two sets containing four and two elements respectively. Then, the number of subsets of the set A × B, each having at least three elements os
[2015]
Option A: 256
Option B: 275
Option C: 510
Option D: 219
Show/Hide Answer Key
Option D: 219
Enter Questions No: 1
If f(x) + 2f(1 / x) = 3x, x ≠ 0, and S = {x ∈ R : f(x) = f(-x)} ; then S
[2016]
Option A: contains exactly one element
Option B: contains exactly two elements
Option C: contains more than two elements
Option D: is an empty set
Show/Hide Answer Key
Option B: contains exactly two elements
Enter Questions No: 1
Let a, b, c ∈ R. If f(x) = ax2 + bx + c is such that a + b + c = 3 and f(x + y) = f(x) + f(y) + xy, for all x, y ∈ R, then
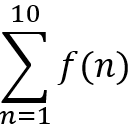
[2017]
Option A: 330
Option B: 165
Option C: 190
Option D: 255
Show/Hide Answer Key
Option A: 330
Enter Questions No: 1
The function f : R → [-1/2, 1/2] defined as f(x) = x / (1 + x2) is
[2017]
Option A: invertible
Option B: injective but not surjective
Option C: surjective but not injective
Option D: neither injective nor surjective
Show/Hide Answer Key
Option C: surjective but not injective
Enter Questions No: 1
Let f(x) = ax (a > 0) be written as f(x) = f1(x) + f2(x), where f1(x) is an even function and f2(x) is an odd function. Then, f1(x + y) + f2(x – y) equals
[2019]
Option A: 2f1(x)f1(y)
Option B: 2f1(x + y)f1(x – y)
Option C: 2f1(x)f2(y)
Option D: 2f1(x + y)f2(x – y)
Show/Hide Answer Key
Option A: 2f1(x)f1(y)
Enter Questions No: 1
If f(x) = loge((1 – x) / (1 + x)), |x| < 1, then f(2x / (1 + x2)) is equal to
[2019]
Option A: 2f(x)
Option B: 2f(x2)
Option C: f(f(x))2
Option D: –2f(x)
Show/Hide Answer Key
Option A: 2f(x)
Enter Questions No: 1
Let f : R → R be defined by f(x) = x / (1 + x2), Then the range of f is
[2019]
Option A: [-1/2, 1/2]
Option B: R – [-1, 1]
Option C: R – [-1/2, 1/2]
Option D: (-1, 1) – {0}
Show/Hide Answer Key
Option A: [-1/2, 1/2]
Enter Questions No: 1
The domain of the definition of the function f(x) = 1 / (4 – x2) + log10(x3 – x) is
[2019]
Option A: (-1, 0) ∪ (1, 2) ∪ (3, ∞)
Option B: (-2, -1) ∪ (-1, 0) ∪ (2, ∞)
Option C: (-1, 0) ∪ (1, 2) ∪ (2, ∞)
Option D: (1, 2) ∪ (2, ∞)
Show/Hide Answer Key
Option C: (-1, 0) ∪ (1, 2) ∪ (2, ∞)
Enter Questions No: 1
Let f(1, 3) → R be a function defined by f(x) = x[x] / (1 + x2), where [x] denotes the greatest integer ≤ x. Then, the range of f is
[2020]
Option A: (2/5, 3/5) ∪ (3/4, 4/5)
Option B: (2/5, 1/2) ∪ (3/5, 4/5)
Option C: (2/5, 4/5)
Option D: (3/5, 4/5)
Show/Hide Answer Key
Option B: (2/5, 1/2) ∪ (3/5, 4/5)
Enter Questions No: 1
Let f(x) be a quadratic polynomial such that f(-1) + f(2) = 0. If one of the roots of f(x) = 0 is 3, then its other root is lies in
[2020]
Option A: (-1, 0)
Option B: (1, 3
Option C: (-3, -1)
Option D: (0, 1)
Show/Hide Answer Key
Option A: (-1, 0)
Enter Questions No: 1
Let [t] denote the greatest integer ≤ t. Then, the equation in x, [x]2 + [x + 2] – 7 = 0 has
[2020]
Option A: exactly two solutions
Option B: exactly four integral solutions
Option C: no integral solutions
Option D: infinitely many solutions
Show/Hide Answer Key
Option D: infinitely many solutions
Enter Questions No: 1
If R = {(x, y) : x, y ∈ Z, x2 + 3y2 ≤ 8} is a relation on the set of integers Z, then the domain of R-1 is
[2020]
Option A: {-2, -1, 1, 2}
Option B: {0, 1}
Option C: {-2, -1, 0, 1, 2}
Option D: {-1, 0, 1}
Show/Hide Answer Key
Option D: {-1, 0, 1}
Enter Questions No: 1
The domain of the function f(x) = sin-1(|x| + 5)/(x2 + 1) is (-∞, -a] ∪ [a, ∞), Then a is equal to
[2020]
Option A: √17 / 2
Option B: (√17 – 1) / 2
Option C: (√17 + 1) / 2
Option D: √17 / 2 + 1
Show/Hide Answer Key
Option C: (√17 + 1) / 2