JEE Main 2020 Question Paper Answer Keys Solutions 3 September Evening Shift
Hi Students, welcome to Amans Maths Blogs (AMB). On this post, you will get JEE Main 2020 Question Paper Answer Keys Solutions 3 September Evening Shift. As you know that Joint Entrance Examination means JEE Main and JEE Advanced is one of the most important entrance exam in engineering entrance examination. JEE Main 2020 is Computer Based Test (CBT) and it was conducted by the National Testing Agency (NTA). JEE Main 2020 exam duration is three hours and the exam consists of 300 marks (Maximum Marks). JEE Main 2020 Questions Paper has 2 sections in all three Subject Papers (Physics, Chemistry, Mathematics) and each subject has 25 questions.
JEE Main 2020 Physics Questions Paper with Answer Keys & Solutions
In JEE Main 2020 Question Paper Answer Keys Solutions 3 September Evening Shift, Physics question paper’s answer keys and solutions by Resonance.
JEE Main 2020 Physics Question Paper with Answer Keys and Solutions (By Resonance)
JEE Main 2020 Chemistry Questions Paper with Answer Keys & Solutions
In JEE Main 2020 Question Paper Answer Keys Solutions 2 September Evening Shift, Chemistry question paper’s answer keys and solutions by Resonance.
JEE Main 2020 Chemistry Question Paper with Answer Keys and Solutions (By Resonance)
JEE Main 2020 Mathematics Questions Paper with Answer Keys & Solutions
In JEE Main 2020 Question Paper Answer Keys Solutions 3 September Evening Shift, Mathematics question paper’s answer keys and solutions by Amans Maths Blogs (AMB).
Instructions for SECTION 1 : (Maximum Marks : 80):
This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4) for its answer, out of which Only One is correct.
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 1
Let A be a 3 x 3 matrix such that
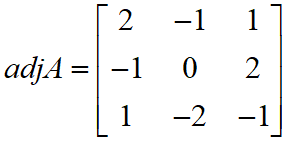
and B = adj (adj A). If |A| = λ and |(B-1)T| = μ, then ordered pair, (|λ|, μ) is equal to
Options:
A. (3, 1/81)
B. (9, 1/9)
C. (3, 81)
D. (9, 1/81)
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 3rd Sep Shift 2 : Ques No 2
If x3dy + xy.dx = x2dy + 2ydx ; y(2) = e and x > 1, then y(4) is equal to
Options:
A. √e / 2
B. 1/2 + √e
C. 3√e / 2
D. 3/2 + √e
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 3
If the sum of the series 20 + 19 3/5 + 19 1/5 + 18 4/5 + … upto nth term is 488 and the nth term is negative, then :
Options:
A. nth term is -4 2/5
B. n = 41
C. nth term is -4
D. n = 60
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 3rd Sep Shift 2 : Ques No 4
The set of all real values of λ for which the quadratic equation (λ2 + 1) x2 – 4λx + 2 = 0 always have
exactly one root in the interval (0, 1) is :
Options:
A. (-3, -1)
B. (0, 2)
C. (1, 3]
D. (2, 4]
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 5
Let R1 and R2 be two relations defined as follows : R1 = {(a, b) ∈ R2 : a2 + b2 ∈ Q} and R2 = {(a, b) ∈ R2 : a2 + b2 ∉ Q}, where Q is the set of all rational numbers, then
Options:
A. R1 is transitive but R2 is not transitive
B. R2 is transitive but R1 is not transitive.
C. Neither R1 nor R2 is transitive
D. R1 and R2 are both transitive.
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 3rd Sep Shift 2 : Ques No 6
The Plane which bisects the line joining the points (4, –2, 3) and (2, 4, –1) at right angles also passes through the point :
Options:
A. (0, –1, 1)
B. (4, 0, –1)
C. (4, 0, 1)
D. (0, 1, –1)
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 7
Let p, q, r be three statements such that the truth value of (p ∧ q) → (~ q V r) is F. Then the truth values of p, q, r are respectively :
Options:
A. T, T, F
B. T, T, T
C. T, F, T
D. F, T, F
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 3rd Sep Shift 2 : Ques No 8
If a triangle ABC has vertices A (–1, 7), B (–7, 1) and C (5, –5), then its orthocentre has coordinates
Options:
A. (-3, 3)
B. (3, -3)
C. (-3/5, 3/5)
D. (3/5, -3/5)
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 9
Suppose f(x) is a polynomial of degree four, having critical points at –1, 0, 1. If T = {x ∈ R |f(x) = f(0)}, then the sum of squares of all the elements of T is :
Options:
A. 4
B. 6
C. 2
D. 8
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 3rd Sep Shift 2 : Ques No 10
If the term independent of x in the expansion of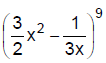 
is k, then 18k is equal to
Options:
A. 11
B. 5
C. 9
D. 7
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 11
If z1, z2 are complex numbers such that Re(z1) = |z1 – 1| and Re(z2) = |z2 – 1| and arg (z1 – z2) =
π/6, then Im (z1 + z2) is equal to :
Options:
A. 2√3
B. √3 / 2
C. 1 / √3
D. 2 / √3
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 3rd Sep Shift 2 : Ques No 12
Let xi (1 ≤ i ≤ 10) be ten observation of a random variable X. If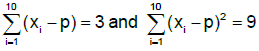 
where 0 ≠ p ∈ R, then the standard deviation of these observations is:
Options:
A. 4/5
B. √(3/5)
C. 9/10
D. 7/10
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 13
The probability that a randomly chosen 5-digit number is made from exactly two digits is:
Options:
A. 135 / 104
B. 150 / 104
C. 134 / 104
D. 121 / 104
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 3rd Sep Shift 2 : Ques No 14
Let a, b, c ∈ R be such that a2 + b2 + c2 = 1. If a cos θ = b cos (θ + 2π/3) = c cos (θ + 4π/3), where θ = π/9, then the angle between the vectors ai + bj + ck and bi + cj + ak is
Options:
A. 0
B. 2π/3
C. π/2
D. π/9
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 15
If the surface area of a cube is increasing at a rate of 3.6 cm2/sec, retaining its shape; then the rate of change of its volume (in cm3/sec.), when the length of a side of the cube is 10 cm, is:
Options:
A. 20
B. 10
C. 18
D. 9
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 3rd Sep Shift 2 : Ques No 16
, (a ≠ 0) is equal to:
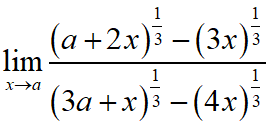
Options:
A. (2/9)(2/3)1/3
B. (2/3)4/3
C. (2/9)1/3
D. (2/3)(2/9)1/3
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 17
Let e1 and e2 be the eccentricities of the ellipse, x2 / 25 + y2 / b2 = 1 (b < 5) and the hyperbola, x2 / 16 – y2 / b2 = 1, respectively satisfying e1e2 = 1. If α and β are the distances between the foci of the ellipse and the foci of the hyperbola respectively, then the ordered pair (α, β) is equal to:
Options:
A. (8, 10)
B. (20/3, 12)
C. (8, 12)
D. (24/5, 10)
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 3rd Sep Shift 2 : Ques No 18
If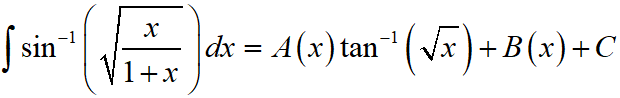 
where C is a constant of integration, then the ordered pair (A(x), B(x)) can be :
Options:
A. (x – 1, √x)
B. (x – 1, -√x)
C. (x + 1, √x)
D. (x + 1, -√x)
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 19
If the value of the integral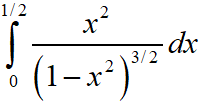 
is k/6, then k is equal to
Options:
A. 2√3 + π
B. 2√3 – π
C. 3√2 + π
D. 3√2 – π
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 3rd Sep Shift 2 : Ques No 20
Let the latus rectum of the parabola y2 = 4x be the common chord to the circles C1 and C2 each of them having radius 2√5. Then, the distance between the centres of the circles C1 and C2 is:
Options:
A. 12
B. 8
C. 8√5
D. 4√5
Answer Key:
Solution:
Instructions for SECTION 2 : (Maximum Marks : 20):
This section contains FIVE (05) questions. The answer to each question is NUMERICAL VALUE with two digit integer and decimal upto one digit.
If the numerical value has more than two decimal places truncate/round-off the value upto TWO decimal places.
Full Marks : +4 If ONLY the correct option is chosen
Zero Marks : 0 In all other cases
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 21
If the tangent to the curve, y = ex at a point (c, ec) and the normal to the parabola, y2 = 4x at the point (1,2) intersect at the same point on the x-axis, then the value of c is…..
Answer Key: 04.00
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 3rd Sep Shift 2 : Ques No 22
Let a plane P contain two lines r = i + λ(i + j), λ ∈ R and r = –j + μ(j – k), μ ∈ R. If Q(α, β, γ) is the foot of the perpendicular drawn from the point M(1, 0, 1) to P, then 3(α + β + γ) equals to
Answer Key: 05.00
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 23
If m arithmetic means (A.Ms) and three geometric means (G.Ms) are inserted between 3 and 243 such that 4th A.M. is equal to 2nd G.M., then m is equal to :
Answer Key: 39.00
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 3rd Sep Shift 2 : Ques No 24
The total number of 3-digit numbers, whose sum of digits is 10, is…….
Answer Key: 54.00
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 3rd Sep Shift 2 : Ques No 25
Let S be the set of all integer solutions, (x, y, z), of the system of equations: x – 2y + 5z = 0, –2x + 4y + z = 0, –7x + 14y + 9z = 0 Such that 15 ≤ x2 + y2 + z2 ≤ 150. Then, the number of elements in the set S is equal to….
Answer Key: 08.00
Solution:
