JEE Main 2020 Question Paper Answer Keys Solutions 2 September Evening Shift
Hi Students, welcome to Amans Maths Blogs (AMB). On this post, you will get JEE Main 2020 Question Paper Answer Keys Solutions 2 September Evening Shift. As you know that Joint Entrance Examination means JEE Main and JEE Advanced is one of the most important entrance exam in engineering entrance examination. JEE Main 2020 is Computer Based Test (CBT) and it was conducted by the National Testing Agency (NTA). JEE Main 2020 exam duration is three hours and the exam consists of 300 marks (Maximum Marks). JEE Main 2020 Questions Paper has 2 sections in all three Subject Papers (Physics, Chemistry, Mathematics) and each subject has 25 questions.
JEE Main 2020 Physics Questions Paper with Answer Keys & Solutions
In JEE Main 2020 Question Paper Answer Keys Solutions 2 September Morning Shift, Physics question paper’s answer keys and solutions by Resonance.
JEE Main 2020 Physics Question Paper with Answer Keys and Solutions (By Resonance)
JEE Main 2020 Chemistry Questions Paper with Answer Keys & Solutions
In JEE Main 2020 Question Paper Answer Keys Solutions 2 September Morning Shift, Chemistry question paper’s answer keys and solutions by Resonance.
JEE Main 2020 Chemistry Question Paper with Answer Keys and Solutions (By Resonance)
JEE Main 2020 Mathematics Questions Paper with Answer Keys & Solutions
In JEE Main 2020 Question Paper Answer Keys Solutions 2 September Evening Shift, Mathematics question paper’s answer keys and solutions by Amans Maths Blogs (AMB).
Instructions for SECTION 1 : (Maximum Marks : 80):
This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4) for its answer, out of which Only One is correct.
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 1
Let S be the sum of the first 9 term of the series : {x + ka} + {x2 + (k + 2)a} + {x3 + (k + 4)a} + {x4 + (k + 6)a} + …….. where a ≠ 0 and x ≠ 1.
If
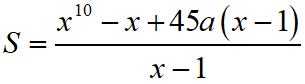
Options:
A. –3
B. 1
C. –5
D. 3
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 2 : Ques No 2
The imaginary part of 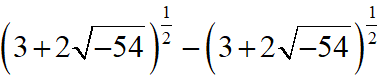
Options:
A. √(-6)
B. √6
C. -2√6
D. 6
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 3
A plane passing through the point (3,1,1) contains two lines whose direction ratios are 1, – 2, 2 and 2, 3,–1 respectively. If this plane also passes through the point(α,–3,5), then α is equal to
Options:
A. 5
B. 10
C. –5
D. –10
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 2 : Ques No 4
The equation of the normal to the curve y = (1 + x)2y + cos2(sin–1 x) at x = 0 is :
Options:
A. y = 4x + 2
B. y + 4x = 2
C. x + 4y = 8
D. 2y + x = 4
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 5
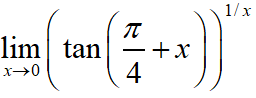
Options:
A. 2
B. 1
C. e
D. e2
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 2 : Ques No 6
For some θ ∈ (0, π/2), if the eccentricity of the hyperbola, x2 – y2 sec2θ = 10 is √5 times the
eccentricity of the ellipse , x2sec2θ + y2 = 5, then the length of the latus rectum of the ellipse, is
Options:
A. 2√5 / 3
B. 2√6
C. 4√5 / 3
D. √30
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 7
Which of the following is a tautology ?
Options:
A. (~p) ∧ (p ∨ q) → q
B. (q → p) ∨ ~(p → q)
C. ~q ∨ (p ∧ q) → q
D. (p → q) ∧ (q → p)
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 2 : Ques No 8
Let EC denote the complement of an event E. Let E1, E2 and E3 be any pairwise independent events with P(E1) > 0 and P(E1 ∩ E2 ∩ E3) = 0 then (E3C ∩ E3C/E1) is equal to
Options:
A. P(E3C) – P(E2)
B. P(E3C) – P(E2C)
C. P(E3) – P(E2C)
D. P(E2C) – P(E3)
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 9
Let A = {x = (x, y, z)T : PX = 0 and x2 + y2 + z2 = 1}, where
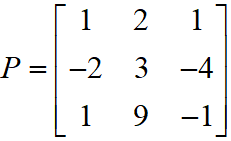
Options:
A. is a singleton.
B. contains more than two elements.
C. contains exactly two elements.
D. is an empty set.
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 2 : Ques No 10
If a curve y = f(x), passing through the point (1,2), is the solution of the differential equation 2x2dy = (2xy + y2) dx, then f(1/2) is equal to
Options:
A. 1/(1 – loge2)
B. 1 + loge2
C. 1/(1 + loge2)
D. -1/(1 + loge2)
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 11
Let a, b, c ∈ R be all non-zero satisfy a3 + b3 + c3 = 2. If the matrix
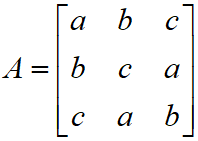
Options:
A. 1/3
B. -1/3
C. 3
D. 2/3
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 2 : Ques No 12
If the equation cos4θ + sin4θ + λ = 0 has real solutions for θ, then λ lies in interval :
Options:
A. (-5/4, -1)
B. [-1, -1/2]
C. (-1/2, -1/2]
D. [-3/2, -5/4]
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 13
Consider a region R = {(x, y) ∈ R2 : x2 ≤ y ≤ 2x}. If a line y = α divides the area of region R into two equal parts, then which of the following is true ?
Options:
A. 3α2 – 8α + 8 = 0
B. 3α3 – 6α3/2 – 16 = 0
C. 3α3 – 6α2 + 16 = 0
D. 3α2 – 8α3/2 + 8 = 0
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 2 : Ques No 14
The set of all possible values of θ in the interval (0, π) for which the points (1,2) and (sinθ, cosθ) lie on the same side of the line x + y = 1 is
Options:
A. (0, π/2)
B. (0, π/4)
C. (π/4, 3π/4)
D. (0, 3π/4)
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 15
Let f(x) be a quadratic polynomial such that f(–1) + f(2) = 0. If one of the roots of f(x) = 0 is 3, then its other root lies in :
Options:
A. (1, 3)
B. (-1, 0)
C. (-3, -1)
D. (0, 1)
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 2 : Ques No 16
The area (in sq. units) of an equilateral triangle inscribed in the parabola y2 = 8x, with one of its vertices on the vertex of this parabola is :
Options:
A. 64√3
B. 192√3
C. 128√3
D. 256√3
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 17
Let f : R → R be a function which satisfies f(x + y) = f(x) + f(y) ∀ x, y ∈ R. If f(1) = 2 and
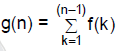
Options:
A. 9
B. 20
C. 5
D. 4
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 2 : Ques No 18
If the sum of first 11 terms of an A.P. , a1, a2, a3 ….. is 0 (a1 ≠ 0), then the sum of the A.P., a1, a3, a5, ….. a23 is ka1 , where k is equal to :
Options:
A. 121/10
B. -121/10
C. -72/10
D. 72/5
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 19
Let n > 2 be an integer. Suppose that there are n Metro stations in a city located around a circular path. Each pair of nearest stations is connected by a straight track only. Further, each pair of nearest station is connected by blue line, whereas all remaining pairs of stations are connected by red line. If number of red lines is 99 times the number of blue lines, then the value of n is
Options:
A. 199
B. 101
C. 201
D. 200
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 2 : Ques No 20
Let f : (–1, ∞) → R be defined by f(0) = 1 and f(x) = [loge(1 + x)] / x, x ≠ 0, then the function is
Options:
A. increases in (–1,0) and decreases in (0,∞).
B. decreases in (–1,∞)
C. decreases in (–1,0) and increases in (0,∞).
D. increases in (–1,∞)
Answer Key:
Solution:
Instructions for SECTION 2 : (Maximum Marks : 20):
This section contains FIVE (05) questions. The answer to each question is NUMERICAL VALUE with two digit integer and decimal upto one digit.
If the numerical value has more than two decimal places truncate/round-off the value upto TWO decimal places.
Full Marks : +4 If ONLY the correct option is chosen
Zero Marks : 0 In all other cases
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 21
Let the position vectors of points ‘A’ and ‘B’ be i + j + k and 2i + j + 3k, respectively. A point P divides the line segment AB internally in the ratio λ : 1 (λ > 0). If O is the origin and OB.OP – 3|OA x OP|2 = 6, then λ is equal to
Answer Key: 00.80
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 2 : Ques No 22
Let [t] denote the greatest integer less than or equal to t. Then the value of 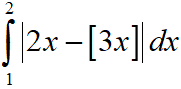
Answer Key: 1
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 23
For a positive integer n, (1 + 1/x)n, is expanded in increasing powers of x. If three consecutive
coefficients in this expansion are in the ratio, 2 : 5 : 12 , then n is equal to _______
Answer Key: 118
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 2 : Ques No 24
If 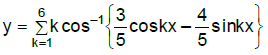
Answer Key: 91
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 25
If the variance of the terms in an increasing A.P. b1 , b2 , b3 , …….. , b11 is 90, then the common
difference of this A.P. is
Answer Key: 3
Solution:

