JEE Main 2020 Question Paper Answer Keys Solutions 2 September Morning Shift
Hi Students, welcome to Amans Maths Blogs (AMB). On this post, you will get JEE Main 2020 Question Paper Answer Keys Solutions 2 September Morning Shift. As you know that Joint Entrance Examination means JEE Main and JEE Advanced is one of the most important entrance exam in engineering entrance examination. JEE Main 2020 is Computer Based Test (CBT) and it was conducted by the National Testing Agency (NTA). JEE Main 2020 exam duration is three hours and the exam consists of 300 marks (Maximum Marks). JEE Main 2020 Questions Paper has 2 sections in all three Subject Papers (Physics, Chemistry, Mathematics) and each subject has 25 questions.
JEE Main 2020 Physics Questions Paper with Answer Keys & Solutions
In JEE Main 2020 Question Paper Answer Keys Solutions 2 September Morning Shift, Physics question paper’s answer keys and solutions by Resonance.
JEE Main 2020 Physics Question Paper with Answer Keys and Solutions (By Resonance)
JEE Main 2020 Chemistry Questions Paper with Answer Keys & Solutions
In JEE Main 2020 Question Paper Answer Keys Solutions 2 September Morning Shift, Chemistry question paper’s answer keys and solutions by Resonance.
JEE Main 2020 Chemistry Question Paper with Answer Keys and Solutions (By Resonance)
JEE Main 2020 Mathematics Questions Paper with Answer Keys & Solutions
In JEE Main 2020 Question Paper Answer Keys Solutions 2 September Morning Shift, Mathematics question paper’s answer keys and solutions by Amans Maths Blogs (AMB).
Instructions for SECTION 1 : (Maximum Marks : 80):
This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4) for its answer, out of which Only One is correct.
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 1 : Ques No 1
The sum of the first three terms of a G.P. is S and their product is 27. Then all such S lie in
Options:
A. (–∞, –3] U [9, ∞)
B. (–∞, –9] U [3, ∞)
C. [–3, ∞)
D. (–∞, 9]
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 2
Box I contains 30 cards numbered I to 30 and Box II contains 20 cards numbered 31 to 50. A box is
selected at random and a card is drawn from it. The number on the card is found to be a non-prime
number. The probability that the card was drawn from Box I is :
Options:
A. 2/3
B. 2/5
C. 8/17
D. 4/17
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 1 : Ques No 3
Area (in sq. units) of the region outside |x|/2 + |y|/3 = 1 and inside the ellipse x2/4 + y2/9 = 1 is
Options:
A. 3(π – 2)
B. 3(4 – π)
C. 6(π – 2)
D. 6(4 – π)
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 4
The domain of the function
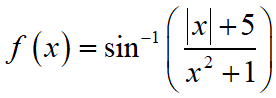
Options:
A. (1 + √17)/2
B. (√17 – 1)/2
C. √17/2
D. √17/2 + 1
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 1 : Ques No 5
If |x| < 1, |y| < 1 and x ≠ y, then the sum to infinity of the following series (x + y) + (x2 + xy + y2) + (x3 + x2y + xy2 + y3) + ….. is :
Options:
A. (x + y + xy) / (1 – x)(1 – y)
B. (x + y – xy) / (1 – x)(1 – y)
C. (x + y – xy) / (1 – x)(1 + y)
D. (x + y + xy) / (1 + x)(1 + y)
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 6
The value of 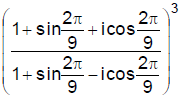
Options:
A. -(√3 – i)/2
B. (√3 – i)/2
C. (1 – i√3)/2
D. -(1 – i√3)/2
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 1 : Ques No 7
Let y = y(x) be the solution of the differential equation (2 + sin x)/(y + 1) (dy/dx) = – cos x, y > 0, y(0) = 1. If y(π) = a and dy/dx at x = π is b, then the order pair (a, b) is equal to
Options:
A. (2, 3/2)
B. (1, -1)
C. (2, 1)
D. (1, 1)
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 8
The plane passing through the points (1, 2, 1), (2, 1, 2) and parallel to the line, 2x = 3y, z = 1 also
passes through the point :
Options:
A. (2, 0, -1)
B. (0, 6, -2)
C. (0, -6, 2)
D. (-2, 0, 1)
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 1 : Ques No 9
Let α > 0, β > 0 be such that α3 + β2 = 4. If the maximum value of the term independent of x in the
binomial expansion of (αX1/9 + βX1/9) is 10k, then k is equal to :
Options:
A. 176
B. 336
C. 352
D. 84
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 10
If R = {(x, y) : x, y ∈ Z, x2 + 3y2 ≤ 8} is a relation on the set of integers Z, then the domain R–1 is ;
Options:
A. {–1, 0, 1}
B. {–2, –1, 1, 2}
C. {0, 1}
D. {–2, –1, 0, 1, 2}
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 1 : Ques No 11
If p(x) be a polynomial of degree three that has a local maximum value 8 at x = 1 and a local minimum value 4 at x = 2; then p(0) is equal to
Options:
A. -24
B. -12
C. 6
D. 12
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 12
A line parallel to the straight line 2x – y = 0 is tangent to the hyperbola x2 / 4 – y2 / 2 = 1 at the point (x1, y1). Then, x12 + 5y12 is equal to :
Options:
A. 10
B. 5
C. 8
D. 6
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 1 : Ques No 13
The contrapositive of the statement “If I reach the station in time, then I will catch the train” is:
Options:
A. If I will catch the train, then I reach the station in time.
B. If I do not reach the station in time, then ¡ will not catch the train.
C. If I do not reach the station in time, then I will catch the train.
D. If I will not catch the train, then I do not reach the station in time.
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 14
Let P(h, k) be a point on the curve y = x2 + 7x + 2, nearest to the line, y = 3x – 3. Then the equation of the normal to the curve at P is :
Options:
A. x + 3y – 62 = 0
B. x + 3y + 26 = 0
C. x – 3y – 11 = 0
D. x – 3y + 22 = 0
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 1 : Ques No 15
Let A be a 2 × 2 real matrix with entries from {0, 1} and |A| ≠ 0. Consider the following two statements ;
(P) If A ≠ I2, then |A| = –1
(Q) If |A| = 1, then tr(A) = 2
where I2 denotes 2 × 2 identity matrix and tr(A) denotes the sum of the diagonal entries of A. Then :
Options:
A. (P) is true and (Q) are false
B. Both (P) and (Q) are true
C. Both (P) and (Q) are false
D. (P) is false and (Q) is true
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 16
Let S be the set of all λ ∈ R for which the system of linear equations statements ;
2x – y + 2z = 2,
x – 2y + λz = –4,
x + λy + z = 4
has no solution. then the set S
Options:
A. is a singleton
B. contains exactly two elements
C. contains more than two elements
D. is an empty set
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 1 : Ques No 17
If the tangent to the curve y = x + siny at a point (a, b) is parallel to the line joining (0, 3/2) and (1/2, 2) then
Options:
A. |b – a| = 1
B. b = π/2 + a
C. |a + b| = 1
D. b = a
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 18
If a function f(x) defined by 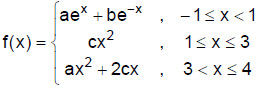
Options:
A. 1/(e2 – 3e + 13)
B. e/(e2 – 3e + 13)
C. e/(e2 – 3e – 13)
D. e/(e2 + 3e + 13)
Answer Key:
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 1 : Ques No 19
Let α and β be the roots of the equation, 5x2 + 6x – 2 = 0. If Sn = αn + βn, n = 1, 2, 3,….., then :
Options:
A. 6S6 + 5S5 = 2S4
B. 5S6 + 6S5 = 2S4
C. 5S6 + 6S5 + 2S4 = 0
D. 6S6 + 5S5 + 2S4 = 0
Answer Key:
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 20
Let X = {x ∈ N : 1 ≤ x ≤ 17} and Y = {ax + b : x ∈ X and a, b ∈ R, a > 0}. If mean and variance of
elements of Y are 17 and 216 respectively then a + b is equal to :
Options:
A. 7
B. 9
C. -7
D. -27
Answer Key:
Solution:
Instructions for SECTION 2 : (Maximum Marks : 20):
This section contains FIVE (05) questions. The answer to each question is NUMERICAL VALUE with two digit integer and decimal upto one digit.
If the numerical value has more than two decimal places truncate/round-off the value upto TWO decimal places.
Full Marks : +4 If ONLY the correct option is chosen
Zero Marks : 0 In all other cases
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 1 : Ques No 21
Let a, b and c be three unit vectors such that |a – c|2 + |a – c|2 = 8. Then, |a + 2b|2 + |a + 2c|2 is equal to
Answer Key: 02.00
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 22
If 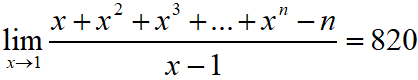
Answer Key: 40.00
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 1 : Ques No 23
The number of integral values of k for which the line, 3x + 4y= k intersects the circle, x2 + y2 – 2x – 4y + 4 = 0 at two distinct points is ….
Answer Key: 09.00
Solution:
JEE Main 2020 Mathematics Questions with Answer Keys and Solutions : Ques No 24
If the letters of the word ‘MOTHER’ be permuted and all the words so formed (with or without meaning) be listed as in a dictionary, then the position of the word ‘MOTHER’ is ……
Answer Key: 309.00
Solution:
JEE Main 2020 Maths Questions Answer Keys Solutions 2nd Sep Shift 1 : Ques No 25
The integral 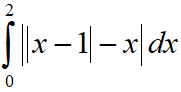
Answer Key: 01.50
Solution:


