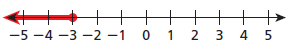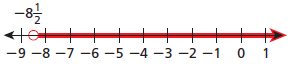Common Core Algebra 1 Unit 3 Inequalities Chapters Summary
Hi Students, Welcome to Amans Maths Blogs (AMB). In this article, you get the full details of Common Core Algebra 1 Unit 3 Inequalities Chapters Summary. It means, I provide you short details of chapters of Common Core Algebra 1 Unit 3 Inequalities. Some definitions and important questions with answers and solutions.
Common Core Algebra 1 Unit 3A Simple Inequalities
Now, there are following chapters in Common Core Algebra 1 Unit 3A Simple Inequalities.
Common Core Algebra 1 Unit 3A Chapter 1 Graphing and Writing Inequalities
In this chapter, we learn basic concepts of inequalities and how to identify the solution of inequalities in one variable.
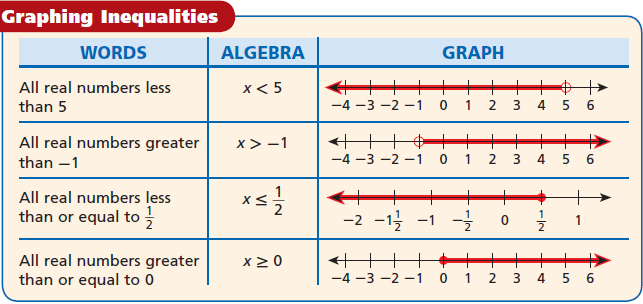
An inequalities is a statement that two quantities are NOT equal.
The following syntax are used to compare the quantities.
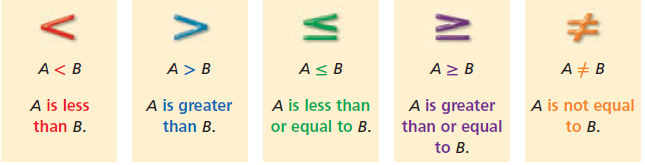
Now a solution of an equality is any value of variable that makes the inequality true, and the solution of a an inequality is represented by a graph on a number line to show all the solutions.
The solutions are shaded and an arrow shows that the solutions continue past those shown on the graph.
To show that an endpoint is a solution, draw a solid circle at that number. To show show that an endpoint is not a solution, draw an empty circle.
Lets understand it by solving some questions:
Common Core Algebra 1 Unit 3 Chapter 1 Question : 1
Graph the inequality: x < -1.5.
Common Core Algebra 1 Unit 3 Chapter 1 Solution : 1
Since x = -1.5 is not in the solution of inequality, we need to draw an empty circle at -1.5, and then shade all the numbers less than -1.5 and draw an arrow pointing to the left.
Thus, required graphing inequality is as below.
Common Core Algebra 1 Unit 3 Chapter 1 Question : 2
Graph the inequality: x >= 2.
Common Core Algebra 1 Unit 3 Chapter 1 Solution : 2
Since x = 2 is in the solution of inequality, we need to draw an solid circle at 2, and then shade all the numbers greater than 2 and draw an arrow pointing to the right.
Thus, required graphing inequality is as below.
Common Core Algebra 1 Unit 3 Chapter 1 Question : 3
Write an inequality shown by the graph.
Common Core Algebra 1 Unit 3 Chapter 1 Solution : 3
We take a variable x.
From the graph, we see that an arrow pointing to left of -3, and a solid circle is at the point -3. Thus, the required inequality is x <= -3.
Common Core Algebra 1 Unit 3 Chapter 1 Question : 4
Write an inequality shown by the graph.
Common Core Algebra 1 Unit 3 Chapter 1 Solution : 4
We take a variable x.
From the graph, we see that an arrow pointing to left of -2, and a solid circle is at the point -2. Thus, the required inequality is x <= -2.
Common Core Algebra 1 Unit 3 Chapter 1 Question : 5
Write an inequality shown by the graph.
Common Core Algebra 1 Unit 3 Chapter 1 Solution : 5
We take a variable x.
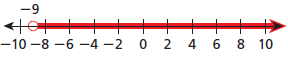
From the graph, we see that an arrow pointing to right of -8 1/2, and a empty circle is at the point -8 1/2. Thus, the required inequality is x > -8 1/2.
Common Core Algebra 1 Unit 3 Chapter 1 Question : 6
Write an inequality shown by the graph.
Common Core Algebra 1 Unit 3 Chapter 1 Solution : 6
We take a variable x.
From the graph, we see that an arrow pointing to left of 5.5, and an empty circle is at the point 5.5. Thus, the required inequality is x < 5.5.
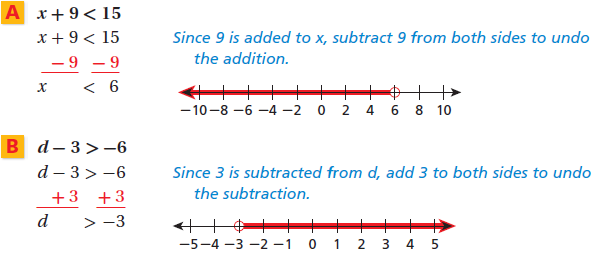
Common Core Algebra 1 Unit 3A Chapter 2 Solving Inequalities by Adding or Subtracting
In this chapter, we learn how to solve inequality by adding or subtracting.
Solving one-step inequalities is much like solving one-step equations.
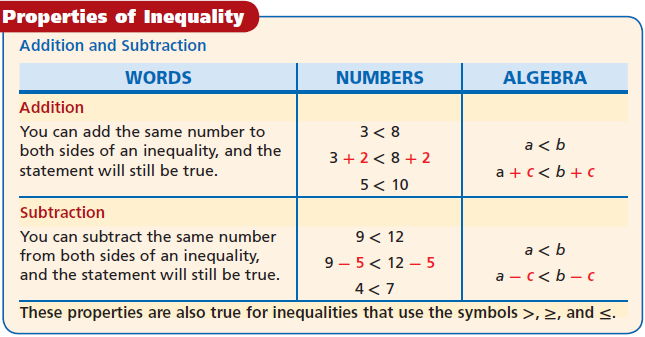
Before this, we need to understand the properties of inequality as below.
To solve an inequality, we need to isolate the variable using properties of inequality and inverse operations.
Lets understand it by solving some questions:
Common Core Algebra 1 Unit 3 Chapter 2 Question : 1
Solve the inequality : x – 3.5 < 7.5.
Common Core Algebra 1 Unit 3 Chapter 2 Solution : 1
Given inequality: x – 3.5 < 7.5
⇒ x – 3.5 + 3.5 < 7.5 + 3.5
⇒ x < 11
Common Core Algebra 1 Unit 3 Chapter 2 Question : 2
Solve the inequality : x + 1 ⩽ 10.
Common Core Algebra 1 Unit 3 Chapter 2 Solution : 2
Given inequality: x + 1 ⩽ 10
⇒ x + 1 – 1 ⩽ 10 – 1
⇒ x ⩽ 9
Common Core Algebra 1 Unit 3 Chapter 2 Question : 3
Solve the inequality : – 45 + x < -30.
Common Core Algebra 1 Unit 3 Chapter 2 Solution : 3
Given inequality: – 45 + x < -30
⇒ -45 + x + 45 < 45 – 30
⇒ x < 15
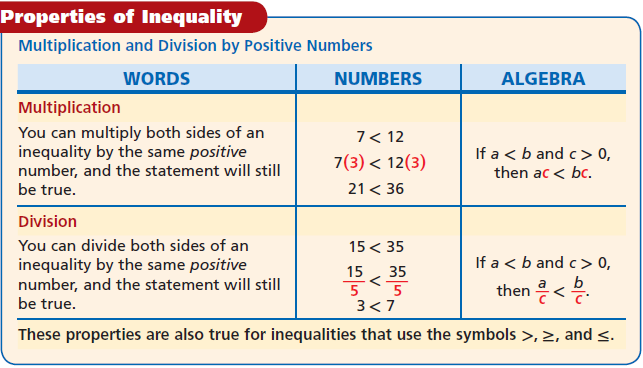
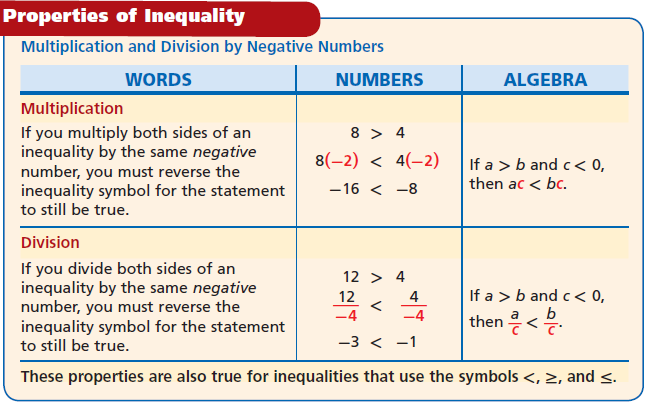
Common Core Algebra 1 Unit 3A Chapter 3 Solving Inequalities by Multiplying or Dividing
In this chapter, we learn how to solve inequality by multiplying or dividing.
To solve an inequality that contains multiplication or division, undo the operation by dividing or multiplying both sides of the inequality by the same number.
The rules for multiplying or dividing by a positive number are as below.
The rules for multiplying or dividing by a negative number are as below.
Lets understand it by solving some questions:
Common Core Algebra 1 Unit 3 Chapter 3 Question : 1
Solve the inequality : 3x > -27.
Common Core Algebra 1 Unit 3 Chapter 3 Solution : 1
Given inequality: 3x > -27
⇒ 3x / 3 > -27 / 3
⇒ x > -9
Common Core Algebra 1 Unit 3 Chapter 3 Question : 2
Solve the inequality : -8x > 72.
Common Core Algebra 1 Unit 3 Chapter 3 Solution : 2
Given inequality: -8x > 72
⇒ -8x / -8 < 72 / -8
⇒ x < -9
Common Core Algebra 1 Unit 3B Compound Inequalities
Now, there are following chapters in Common Core Algebra 1 Unit 3B Compound Inequalities.
Common Core Algebra 1 Unit 3B Chapter 4 Solving Two-Steps & Multi-Steps Inequalities
In this chapter, we learn how to solve inequalities that contain more than one operation.
To solve an inequality that contains more than one operation require more than one step to solve. Use inverse operation to undo the operations in the inequality one at a time.
To solve more complicated inequalities, we need to simplify the expression on one or both sides by using the order of operations, combining like terms or using Distributive property.
Lets understand it by solving some questions:
Common Core Algebra 1 Unit 3 Chapter 4 Question : 1
Solve the inequality : 160 + 4f ⩽ 500.
Common Core Algebra 1 Unit 3 Chapter 4 Solution : 1
Given inequality: 160 + 4f ⩽ 500
⇒ 160 + 4f – 160 ⩽ 500 – 160
⇒ 4f ⩽ 340
⇒ 4f / 4 ⩽ 340 / 4
⇒ f ⩽ 85
Common Core Algebra 1 Unit 3 Chapter 4 Question : 2
Solve the inequality : – 4 + (-8) < -5c – 2.
Common Core Algebra 1 Unit 3 Chapter 4 Solution : 2
Given inequality: – 4 + (-8) < -5c – 2
⇒ – 12 < -5c – 2
⇒ -12 + 2 < -5c – 2 + 2
⇒ -10 < -5c
⇒ -10/-5 > -5c /-5
⇒ 2 > c
⇒ c < 2
Common Core Algebra 1 Unit 3B Chapter 5 Solving Inequalities Variables on Both Sides
In this chapter, we learn how to solve inequalities that contain variables on both sides.
Solving inequalities that contain variables on both sides is same as we learnt to solve the equations containing variables on both sides.
For this, we need to collect all the variables on one side and all the constant term on the other side.
Some inequalities are true for all values of variables. For these inequalities all real numbers are the solutions. For example: (x + 5) > (x + 3)
Some inequalities are false for all values of variables. For these inequalities, there is no solutions. For example: (x + 2) > (x + 1)
Lets understand it by solving some questions:
Common Core Algebra 1 Unit 3 Chapter 5 Question : 1
Solve the inequality : x < 3x + 8.
Common Core Algebra 1 Unit 3 Chapter 5 Solution : 1
Given inequality: x < 3x + 8
⇒ x – x < 3x + 8 – x
⇒ 0 < 2x + 8
⇒ -8 < 2x + 8 – 8
⇒ -8 < 2x
⇒ -8/2 < 2x/2
⇒ -4 < x
⇒ x > -4
Common Core Algebra 1 Unit 3 Chapter 5 Question : 2
Solve the inequality : 2(x + 3) < 5 + 2x.
Common Core Algebra 1 Unit 3 Chapter 5 Solution : 2
Given inequality: 2(x + 3) < 5 + 2x
⇒ 2x + 6 < 5 + 2x
Now, we see that 2x appears on both sides, for any number 2x, adding 6 will never result in a lesser number adding 5.
Thus, there is NO solution for this inequality.
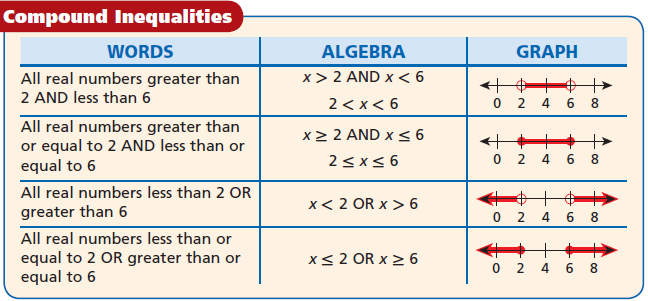
Common Core Algebra 1 Unit 3B Chapter 6 Solving Compound Inequalities
In this chapter, we learn how to solve compound inequalities.
When two simple inequalities are combined into one statement by the words AND or OR, then this type of inequalities is called as compound inequalities.
For example:
The solution of a compound inequality can be represented by a graph. The graph of compound inequality involving AND statement can be done by using the concepts of overlapping region. The overlapping region is called the INTERSECTION and shows the solutions of the both inequalities.
The graph of compound inequality involving OR statement can be done by using the concepts of overlapping region. The overlapping region is called the UNIONS and shows the solutions of the either inequalities.
Lets understand it by solving some questions:
Common Core Algebra 1 Unit 3 Chapter 6 Question : 1
Solve the inequality : 4 ⩽ x + 2 ⩽ 8.
Common Core Algebra 1 Unit 3 Chapter 6 Solution : 1
Given inequality: 4 ⩽ x + 2 ⩽ 8
⇒ 4 ⩽ x + 2 AND x + 2 ⩽ 8
⇒ 4 – 2 ⩽ x + 2 – 2 AND x + 2 – 2 ⩽ 8 – 2
⇒ 2 ⩽ x AND x ⩽ 6
Thus, 2 ⩽ x ⩽ 6
Common Core Algebra 1 Unit 3 Chapter 6 Question : 2
Solve the inequality : -5 ⩽ 2x + 3 ⩽ 9.
Common Core Algebra 1 Unit 3 Chapter 6 Solution : 2
Given inequality: -5 ⩽ 2x + 3 ⩽ 9
⇒ -5 ⩽ 2x + 3 ⩽ 9
⇒ -5 – 3 ⩽ 2x + 3 – 3 ⩽ 9 – 3
⇒ -8 ⩽ 2x ⩽ 6
⇒ -8 / 2 ⩽ 2x / 2 ⩽ 6 / 2
⇒ -4 ⩽ x ⩽ 3
Common Core Algebra 1 Unit 3 Chapter 6 Question : 3
Solve the inequality : -4 + x > 1 OR – 4 + x < -3
Common Core Algebra 1 Unit 3 Chapter 6 Solution : 3
Given inequality: -4 + x > 1 OR – 4 + x < -3
⇒ -4 + x + 4 > 1 + 4 OR – 4 + x + 4 < -3 + 4
⇒ x > 5 OR x < 1
Common Core Algebra 1 Unit 3B Chapter 7 Solving Absolute Inequalities
In this chapter, we learn how to solve inequalities in one variable involving absolute value expression.
An inequality containing absolute value expression can be rewritten as a compound inequality.
For example: The inequality containing absolute expression |x| < 5 can be written as x > -5 AND x < 5. It means – < x < 5.
The method to solve inequality containing ‘<‘ is as below.
The method to solve inequality containing ‘>’ is as below.
Lets understand it by solving some questions:
Common Core Algebra 1 Unit 3 Chapter 7 Question : 1
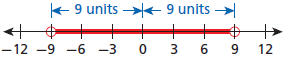
Solve the inequality : |x| + 3 < 12.
Common Core Algebra 1 Unit 3 Chapter 7 Solution : 1
Given inequality: |x| + 3 < 12
⇒ |x| + 3 – 3 < 12 – 3
⇒ |x| < 9
⇒ x > -9 AND x < 9
⇒ – 9 < x < 9
Common Core Algebra 1 Unit 3 Chapter 7 Question : 2
Solve the inequality : |x + 4| <= 2.
Common Core Algebra 1 Unit 3 Chapter 7 Solution : 2
Given inequality: |x + 4| <= 2
⇒ x + 4 >= – 2 AND x + 4 <= 2
⇒ x >= – 6 AND x <= -2
⇒ -6 <= x <= -2