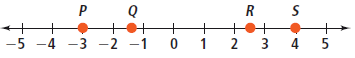Common Core Algebra 1 Unit 1 Foundations For Algebra Chapter Plan
Hi Students, Welcome to Amans Maths Blogs (AMB). In this article, you get the full details of Common Core Algebra 1 Unit 1 Foundations For Algebra Chapter Plan. It means, I describe you about Common Core Algebra 1 Unit 1 Foundations For Algebra, what the chapters and lessons plan. Some definitions and important questions with answers and solutions.
Common Core Algebra 1 Unit 1 Foundations For Algebra Chapters
Now, there are following chapters in Common Core Algebra 1 Unit 1 Foundations For Algebra.
Common Core Algebra 1 Unit 1 Chapter 1 Variables and Expressions
In this chapter, the definitions of variables, constants, algebraic expression and numerical expressions are explained.Common Core Algebra 1 Unit 1 Foundations For Algebra Chapter Plan
A Variable is a letter or symbol used to represent a value that can change.
A Constant is a value that does not change.
A Numerical Expression may contain only constant and/or operation.
An Algebraic Expression may contains variables, constant, and or operations.
Some important questions in this chapter are below.
Common Core Algebra 1 Unit 1 Chapter 1 Question No : 1
What is the algebraic expression for the phrase ” the product of 9 a number t”.
Common Core Algebra 1 Unit 1 Chapter 1 Solution : 1
Required algebraic expression for the given phrase is 9t.
Common Core Algebra 1 Unit 1 Chapter 1 Question No : 2
Write an word phrase for the algebraic expression “2(5 + n)”
Common Core Algebra 1 Unit 1 Chapter 1 Solution : 2
The word phrase for the given algebraic expression is “product of 2 and the sum of 5 and n”.
Common Core Algebra 1 Unit 1 Chapter 1 Question No : 3
Write the algebraic expression for the phrase “8 minus the product of 9 and r”.
Common Core Algebra 1 Unit 1 Chapter 1 Solution : 3
The algebraic expression for the given phrase is (8 – 9r).
Common Core Algebra 1 Unit 1 Chapter 1 Question No : 4
Write an word phrase for the algebraic expression “9n + 1”.
Common Core Algebra 1 Unit 1 Chapter 1 Solution : 4
The word phrase for the given algebraic expression is “1 more than the product of 9 and n”.
Common Core Algebra 1 Unit 1 Chapter 1 Question No : 5
Write the algebraic expression for the phrase “6.7 more than the product of 5 and n”.
Common Core Algebra 1 Unit 1 Chapter 1 Solution : 5
The algebraic expression for the given phrase is (5n + 6.7).
Common Core Algebra 1 Unit 1 Chapter 2 Order of Operations
In this chapter, we need to simplify expressions involving exponents and need to use the order of operations to evaluate expressions. Common Core Algebra 1 Unit 1 Foundations For Algebra Chapter Plan The order of operations is according to as below:
1. Perform any operation(s) inside grouping symbols, such as parentheses ( ) and brackets [ ]. A fraction bar also acts as a grouping symbol.
2. Simplify powers.
3. Multiply and divide from left to right.
4. Add and subtract from left to right.
This order of operations are also known as PEDMAS rule.
Read More About PEDMAS Rule: Click Here.
Some important questions in this chapter are below.
Common Core Algebra 1 Unit 1 Chapter 2 Question No : 1
What is the simplified form of each expression: 23?
Common Core Algebra 1 Unit 1 Chapter 2 Solution : 1
23 = 2 x 2 x 2 = 8
Common Core Algebra 1 Unit 1 Chapter 2 Question No : 2
Evaluate the expression x2 + 2(x + y) for x = 3 and y = 4.
Common Core Algebra 1 Unit 1 Chapter 2 Solution : 2
Put x = 3 and y = 4 in the given expression
x2 + 2(x + y) = (3)2 + 2(3 + 4) = 9 + 14 = 23
Common Core Algebra 1 Unit 1 Chapter 2 Question No : 3
Simplify the expression 52 + 82 – 3(4 – 2)3
Common Core Algebra 1 Unit 1 Chapter 2 Solution : 3
52 + 82 – 3(4 – 2)3 = 25 + 64 – 3(2)3 = 89 – 3×8 = 89 – 24 = 65
Common Core Algebra 1 Unit 1 Chapter 2 Question No : 4
Evaluate the expression 2st2 – s2 for s = 4 and t = 8.
Common Core Algebra 1 Unit 1 Chapter 2 Solution : 4
Put s = 4 and t = 8 in the given expression
2st2 – s2 = 2(4)(8)2 – (4)2 = 512 – 16 = 496
Common Core Algebra 1 Unit 1 Chapter 2 Question No : 5
Evaluate the expression (2a + 2b)2 for a = 3 and b = 4.
Common Core Algebra 1 Unit 1 Chapter 2 Solution : 5
Put a = 3 and b = 4 in the given expression
(2a + 2b)2 = (2×3 + 2×4)2 = (6 + 8)2 = 142 = 196
Common Core Algebra 1 Unit 1 Chapter 3 Real Numbers & Number Line
In this chapter, we need to study about square root, radicand, radical, perfect square, rational numbers, natural numbers etc. Common Core Algebra 1 Unit 1 Foundations For Algebra Chapter Plan
A number a is a square root of a number b if a2 = b.
The radical symbol √ indicates a nonnegative square root, also called a principal square root. The expression under the radical symbol is called the radicand.
The combination of the radical symbol and radicand form a radical.
The square of an integer is called a perfect square. For example, 49 is a perfect square because 72 = 49.
When a radicand is not a perfect square, you can estimate the square root of the radicand.
Read More About Square and Square Root: Click Here.
Rational number is any number that you can write in the form a/b, where a and b are integers and b ≠ 0.
A rational number in decimal form is either a terminating decimal such as 5.45 or a repeating decimal such as 0.41666 . . . .
Read More About Rational Number: Click Here.
Some important questions in this chapter are below.
Common Core Algebra 1 Unit 1 Chapter 3 Question No : 1
Simplify the expression √900.
Common Core Algebra 1 Unit 1 Chapter 3 Solution : 1
√900 = √(22 x 32 x 52) = (2 x 3 x 5) = 30
Common Core Algebra 1 Unit 1 Chapter 3 Question No : 2
Simplify the expression √169.
Common Core Algebra 1 Unit 1 Chapter 3 Solution : 2
√169 = √(132) = 13
Common Core Algebra 1 Unit 1 Chapter 3 Question No : 3
Estimate the square root and Round to the nearest integer. √17.
Common Core Algebra 1 Unit 1 Chapter 3 Solution : 3
The perfect squares closest to 17 are 42 = 16 and 52 = 25.
Since 17 is closer to 16, then √17 ≅ 4.
Common Core Algebra 1 Unit 1 Chapter 3 Question No : 4
A square picture has an area of 225 in.2. What is the side length of the picture?
Common Core Algebra 1 Unit 1 Chapter 3 Solution : 4
The side of the square picture is √225 = 15 in.
Common Core Algebra 1 Unit 1 Chapter 3 Question No : 5
Evaluate the expression 3m2 + n; for the values of the variables : m = 5, n = 3.
Common Core Algebra 1 Unit 1 Chapter 3 Solution : 5
Put m = 5, n = 3 in 3m2 + n, we get
3m2 + n = 3(5)2 + 3 = 3×25 + 3 = 75 + 3 = 78
Common Core Algebra 1 Unit 1 Chapter 4 Properties of Real Numbers
In this chapter, we need to study about
Commutative Properties of Addition and Multiplication,
Associative Properties of Addition and Multiplication,
Identity Properties of Addition and Multiplication,
Zero Property of Multiplication,
Common Core Algebra 1 Unit 1 Foundations For Algebra Chapter Plan
Multiplication Property of -1 etc.
Two algebraic expressions are equivalent expressions if they have the same value for all values of the variable(s).
Some important questions in this chapter are below.
Common Core Algebra 1 Unit 1 Chapter 4 Question No : 1
Name the property that the statement illustrates: 75 + 6 = 6 + 75.
Common Core Algebra 1 Unit 1 Chapter 4 Solution : 1
75 + 6 = 6 + 75, it is commutative property of addition.
Common Core Algebra 1 Unit 1 Chapter 4 Question No : 2
Name the property that the statement illustrates: 27 x p = p x 27.
Common Core Algebra 1 Unit 1 Chapter 4 Solution : 2
27 x p = p x 27, it is commutative property of multiplication.
Common Core Algebra 1 Unit 1 Chapter 4 Question No : 3
What is the simplified form of (1.2 + 0) + 4.6 + 3.8?
Common Core Algebra 1 Unit 1 Chapter 4 Solution : 3
(1.2 + 0) + 4.6 + 3.8 = 1.2 + 4.6 + 3.8 = 5.0 + 4.6 = 9.6
Common Core Algebra 1 Unit 1 Chapter 4 Question No : 4
Tell whether the expressions in each pair are equivalent: 2 + h + 4 and 2 x h x 4.
Common Core Algebra 1 Unit 1 Chapter 4 Solution : 4
Since 2 + h + 4 = 6 + h and 2 x h x 4 = 8h, then the given two expression are NOT equivalent.
Common Core Algebra 1 Unit 1 Chapter 4 Question No : 5
Tell whether the expressions in each pair are equivalent: (3 + 7) + m and m + 10.
Common Core Algebra 1 Unit 1 Chapter 4 Solution : 5
Since (3 + 7) + m = 10 + m and m + 10 = 10 + m, then the given two expression are equivalent.
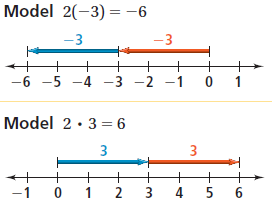
Common Core Algebra 1 Unit 1 Chapter 5 Adding & Subtracting Real Numbers
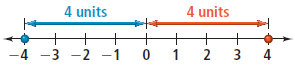
In this chapter, we need to study about the addition and subtraction of real numbers using a number line model.
The absolute value of a number is its distance from 0 on a number line. Absolute value is always nonnegative since distance is always nonnegative.
For example, the absolute value of 4 is 4 and the absolute value of -4 is 4. You can write this as |4| = 4 and |-4| = 4
To add two numbers with the same sign, add their absolute values. The sum has the same sign as the addends. To add two numbers with different signs, subtract their absolute values. The sum has
the same sign as the addend with the greater absolute value. For example:
Some important questions in this chapter are below.
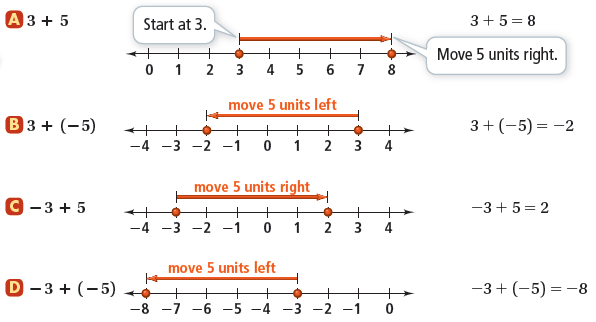
Common Core Algebra 1 Unit 1 Chapter 5 Question No : 1
Find the sum: 17 + (-28)
Common Core Algebra 1 Unit 1 Chapter 5 Solution : 1
Required Sum = 17 + (-28) = -11
Common Core Algebra 1 Unit 1 Chapter 5 Question No : 2
Find the difference: 36 – (-12)
Common Core Algebra 1 Unit 1 Chapter 5 Solution : 2
Required difference = 36 – (-12)
Common Core Algebra 1 Unit 1 Chapter 5 Question No : 3
Evaluate the expression a – b + c for a = – 2, b = -4.1, and c = 5.
Common Core Algebra 1 Unit 1 Chapter 5 Solution : 3
Required value = a – b + c = -2 – (-4.1) + 5 = -2 + 4.1 + 5 = 9.1 – 2 = 7.2
Common Core Algebra 1 Unit 1 Chapter 5 Question No : 4
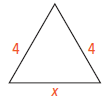
What is an algebraic expression for the perimeter of the triangle?
Common Core Algebra 1 Unit 1 Chapter 5 Solution : 3
Required perimeter of the triangle = 4 + 4 + x = x + 8
Common Core Algebra 1 Unit 1 Chapter 5 Question No : 5
Which point on the number line below is the best estimate for √8.
Common Core Algebra 1 Unit 1 Chapter 5 Solution : 5
Since 2 < √8 < 3, the best estimate for √8 on the number line is point R.
Common Core Algebra 1 Unit 1 Chapter 6 Multiplying & Dividing Real Numbers
In this chapter, we need to study about the multiplication and division of real numbers.
The product of two real numbers with different signs is negative. The product of two real numbers with the same sign is positive.
The quotient of two real numbers with different signs is negative. For example: -20 ÷ 5 = -4
The quotient of two real numbers with the same sign is positive. For example: 20 ÷ 5 = 4
The quotient of 0 and any nonzero real number is 0. For example: 0 ÷ 5 = 0
The quotient of any real number and 0 is undefined. For example: 5 ÷ 0 = Not Defined
Some important questions in this chapter are below.
Common Core Algebra 1 Unit 1 Chapter 6 Question No : 1
A sky diver’s elevation changes by -3600 ft in 4 min after the parachute opens. What is the average change in the sky diver’s elevation each minute?
Common Core Algebra 1 Unit 1 Chapter 6 Solution : 1
Required Change Rate = -3600 ÷ 4 = -900.
Thus, The sky diver’s average change in elevation is -900 ft per minute.
Common Core Algebra 1 Unit 1 Chapter 6 Question No : 2
Find the product: -3(-12)
Common Core Algebra 1 Unit 1 Chapter 6 Solution : 2
Required Product = -3(-12) = 36.
Common Core Algebra 1 Unit 1 Chapter 6 Question No : 3
Find the quotient: 48 ÷ 3
Common Core Algebra 1 Unit 1 Chapter 6 Solution : 3
Required Quotient = 48 ÷ 3 = 16.
Common Core Algebra 1 Unit 1 Chapter 6 Question No : 4
Simplify the expression: -11 + (-11) + (-11).
Common Core Algebra 1 Unit 1 Chapter 6 Solution : 4
Required Simplification = -11 + (-11) + (-11) = -33.
Common Core Algebra 1 Unit 1 Chapter 6 Question No : 5
What is the perimeter of the triangle shown?
Common Core Algebra 1 Unit 1 Chapter 6 Solution : 5
Required Perimeter = 6y + 9 + 15 = 6y + 24.
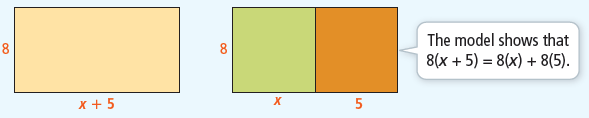
Common Core Algebra 1 Unit 1 Chapter 7 Distributive Property
In this chapter, we need to study about the distributive property.
To solve problems in mathematics, it is often useful to rewrite expressions in simpler forms. The Distributive Property, illustrated by the area model below, is another property of real numbers that helps you to simplify expressions.
We can use the Distributive Property to simplify the product of a number and a sum or difference.
Let a, b, and c be real numbers. Then, using the distributive property, we have algebra
a(b + c) = ab + ac
(b + c)a = ba + ca
a(b – c) = ab – ac
(b – c)a = ba – ca
Some important questions in this chapter are below.
Common Core Algebra 1 Unit 1 Chapter 7 Question No : 1
Use the Distributive Property to simplify the expression: 16(7b + 6)
Common Core Algebra 1 Unit 1 Chapter 7 Solution : 1
16(7b + 6) = (16 x 7b) + (16 x 6) = 112b + 96
Common Core Algebra 1 Unit 1 Chapter 7 Question No : 2
Simplify the expression by combining like terms: 11x + 9x
Common Core Algebra 1 Unit 1 Chapter 7 Solution : 2
Required simplification = (11 + 9)x = 20x
Common Core Algebra 1 Unit 1 Chapter 7 Question No : 3
Simplify the expression by combining like terms: 6yz + 2yz – 8yz
Common Core Algebra 1 Unit 1 Chapter 7 Solution : 3
Required simplification = 6yz + 2yz – 8yz = (6 + 2 – 8)yz = 0yz = 0
Common Core Algebra 1 Unit 1 Chapter 7 Question No : 4
Simplify the expression by combining like terms: 6yz + 2yz – 8yz
Common Core Algebra 1 Unit 1 Chapter 7 Solution : 4
Required simplification = 6yz + 2yz – 8yz = (6 + 2 – 8)yz = 0yz = 0
Common Core Algebra 1 Unit 1 Chapter 7 Question No : 5
Simplify the expression by combining like terms: 5(2d + 1) + 7(5d + 3)
Common Core Algebra 1 Unit 1 Chapter 7 Solution : 5
Required simplification = 5(2d + 1) + 7(5d + 3) = 10d + 5 + 35d + 21 = d(10 + 35) + (5 + 21) = 45d + 26
Common Core Algebra 1 Unit 1 Chapter 8 An Introduction to Equations
In this chapter, we will learn about the equations.
An equation is a mathematical sentence that uses an equal sign (=).
An equation is true if the expressions on either side of the equal sign are equal (1 + 1 = 2, x + x = 2x).
An equation is false if the expressions on either side of the equal sign are not equal (1 + 1 = 3, x + x = 3x).
An equation is an open sentence if it contains one or more variables and may be true or false depending on the values of its variables. (2x – 14 = 54).
A solution of an equation containing a variable is a value of the variable that makes the equation true.
Some important questions in this chapter are below.
Common Core Algebra 1 Unit 1 Chapter 8 Question No : 1
Tell whether the equation is true, false, or open: 85 + (-10) = 95
Common Core Algebra 1 Unit 1 Chapter 8 Solution : 1
LHS = 85 + (-10) = 85 – 10 = 75 and RHS = 95
Since LHS ≠ RHS, thus, the given equation is false.
Common Core Algebra 1 Unit 1 Chapter 8 Question No : 2
Tell whether the equation is true, false, or open: -8(-2) – 7 = 14 – 5
Common Core Algebra 1 Unit 1 Chapter 8 Solution : 2
LHS = -8(-2) – 7 = 16 – 7 = 9 and RHS = 14 – 5 = 9
Since LHS = RHS, thus, the given equation is true.
Common Core Algebra 1 Unit 1 Chapter 8 Question No : 3
Tell whether the equation is true, false, or open: 5x + 7 = 17
Common Core Algebra 1 Unit 1 Chapter 8 Solution : 3
Since the equation contains a variable x, then the given equation is open.
Common Core Algebra 1 Unit 1 Chapter 8 Question No : 4
Tell whether x = 3 is a solution of the equation 8x + 5 = 29.
Common Core Algebra 1 Unit 1 Chapter 8 Solution : 4
Put x = 3 in LHS of 8x + 5 = 29, we get
LHS = 8(3) + 5 = 29 = RHS
Thus, x = 3 is the solution of the given equation.
Common Core Algebra 1 Unit 1 Chapter 8 Question No : 5
Tell whether b = -3 is a solution of the equation 5b + 1 = 16.
Common Core Algebra 1 Unit 1 Chapter 8 Solution : 5
Put b = -3 in LHS of 5b + 1 = 16, we get
LHS = 5b + 1 = 5(-3) + -15 + 1 = -14 ≠ 16 = RHS
Thus, b = -3 is NOT the solution of the given equation.
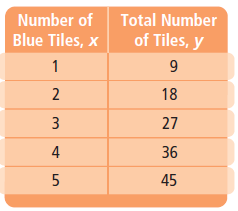
Common Core Algebra 1 Unit 1 Chapter 9 Pattern Equations & Graphs
In this chapter, we will discuss about the relation between two variables by observing the pattern.
An equation with two variables can represent the relationship between two varying quantities.
A solution of an equation with two variables x and y is any ordered pair (x, y) that makes the equation true.
Inductive reasoning is the process of reaching a conclusion based on an observed pattern. You can use inductive reasoning to predict values.
For example: The table shows the relationship between the number of blue tiles and the total number of tiles in each figure. Extend the pattern. What is the total number of tiles in a figure with 8 blue tiles?
By observing the pattern of values in the table, we get that y = 9x.
Thus, to find the total number of tiles in the given figure with 8 blue tiles, put x = 8 in y = 8x.
Therefore, y = 9(8) = 72.
Some important questions in this chapter are below.
Common Core Algebra 1 Unit 1 Chapter 9 Question No : 1
Tell whether the given equation y = x + 6; has the ordered pair (0, 6) as a solution.
Common Core Algebra 1 Unit 1 Chapter 9 Solution : 1
Put x = 0 and y = 6 in the given equation. We get that
LHS = y = 6 and RHS = x + 6 = 0 + 6 = 6.
Since LHS = RHS, So YES the given ordered pair is the solution of the given equation.
Common Core Algebra 1 Unit 1 Chapter 9 Question No : 2
What is the value of -34?
Common Core Algebra 1 Unit 1 Chapter 9 Solution : 2
The value of -34 = -(3 x 3 x 3 x 3) = -81