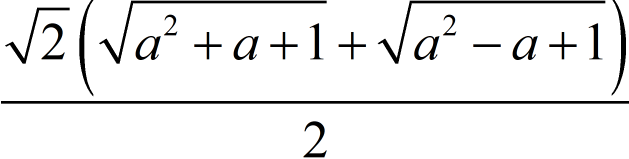Pre RMO Sample Papers With Answer Keys

In this post, some important questions of Pre RMO Sample Papers With Answer Keys are given. 

Read: Pre RMO and RMO Important Study Materials: Books | PDFs | Blogs | YouTube Channels | Solved Papers

Pre RMO Sample Papers with Answer Keys Question No 1:

When a three digit number is divided by 2, 3, 4, 5 and 7, the remainders are all 1. Find the minimum and maximum values of such three digit numbers.

Solution:

Pre RMO Sample Papers with Answer Keys Question No 2:

Find the remainder of the number  when divided by 7

Solution:

Pre RMO Sample Question No 3:

If (x –1) (x + 3) (x –4) (x – 8) + m is a perfect square, then m is?

Solution:

Pre RMO Sample Question No 4:

If n + 20 and n – 21 are both perfect squares, where n is a natural number, find n.

Solution:

Pre RMO Sample Question No 5:

If a four digit number and the sum of its all digits have a sum 2006, find the four digit number

Solution:

Pre RMO Sample Question No 6:

Given that the equation 4x/3 – a = 2x/5 + 140 has a positive integer solution, where a is a parameter. Find the minimum positive integer value of a.

Solution:

Pre RMO Sample Question No 7:

Find the positive integer solutions to the equation 12x + 5y = 125.

Solution:

Read More : Pre RMO 2019 Results & Cut Off Marks

Pre RMO Sample Question No 8:

Find the general solution of Diophantine equation 71x + 83y = 5

Solution:

Pre RMO Sample Question No 9:

A four digit number has remainder 13 when divided by 16, and has remainder 122 when divided by 125. Find the minimum value of such four digit numbers.

Solution:

Pre RMO Sample Question No 10:

Determine if there is a natural number k such that the sum of the two numbers 3k² + k – 4 and 7k² – 3k+ 1 is a perfect square.

Solution:

Pre RMO Sample Question No 11:

Let S = , then find the value of .

Solution:

Pre RMO Sample Question No 12:

If the sum of 2009 consecutive positive integers is a perfect square, find the minimum value of the maximum number of the 2009 numbers.

Solution:

Pre RMO Sample Question No 13:

Solve the equation 2[x] = x + 2{x}.

Solution:

Pre RMO Sample Question No 14:

The digits 1, 2, 3, 4, and 5 are each used once to compose a five-digit number abcde such that the
three digit number abc is divisible by 4, bcd divisible by 5, and cde is divisible by 3. Find the digit a.

Solution:

Pre RMO Sample Question No 15:

Let abcdef be a 6-digit integer such that defabc is 6 times the value of abcdef. Find the value of a +b + c + d + e + f.

Solution:

Pre RMO Sample Question No 16:

Find all the natural number n such that n² – 19n + 91 is a perfect square.

Solution:

Pre RMO Sample Question No 17:

What is the smallest positive integer n > 1 such that 3n ends with 003?

Solution:

Pre RMO Sample Question No 18:

Find all the positive integers n, such that n × 2ⁿ + 1 is divisible by 3.

Solution:

Pre RMO Sample Question No 19:

Given that five digit number 2x9y1 is a perfect square number. Find the value of 3x + 7y..

Solution:

Pre RMO Sample Question No 20:

Find the remainder of (257³³ + 46)²⁶ when it is divided by 50.

Solution:

Pre RMO Sample Question No 21:

Find the smallest positive integer n such that 1000 <= n <= 1100 and 1111ⁿ + 1222ⁿ + 1333ⁿ + 1444ⁿ is divisible by 10.

Solution:

Pre RMO Sample Question No 22:

Simplify M = .

Solution:

Pre RMO Sample Question No 23:

Simplify .

Solution:

Pre RMO Sample Question No 24:

Simplify .

Solution:

Pre RMO Sample Question No 25:

Find the last two digits of .

Solution:

Pre RMO Sample Question No 26:

What is the remainder of 123456789⁴ when it is divided by 8?

Solution:

Pre RMO Sample Question No 27:

Simplify 

Solution:

Pre RMO Sample Question No 28:

Find the number of positive integer n, such that the remainder is 7 when 2007 is divided by n.

Solution:

Pre RMO Sample Question No 29:

Find the remainder of  when it is divided by 11.

Solution:

Pre RMO Sample Question No 30:

It is known that 2726, 4472, 5054, 6412 have the same remainder when they are divided by some two digit natural number m. Find the value of m

Solution:

Answers:

1__ Min = 421 and Max = 841

2__ 6

3__ 196

4__ 421

5__ 1984

6__ Min Value of a = 14

7__ (5, 13) and (10, 1)

8__ x = -29 + 83t, y = 6 – 17t

9__ 1997

10__ Does Not Exist

11__ 241

12__ 1045

13__ x = 0, 4/3, 8/3

14__ 1

15__ 27

16__ 9 or 10

17__ 101

18__ 6k + 1 or 6k + 2, k = 0, 1, 2…

19__ 29

20__ 29

21__ 1001

22__ 

23__ 

24__ 36

25__ 88

26__ 1

27__ 

28__ 16

29__ 9

30__ 97