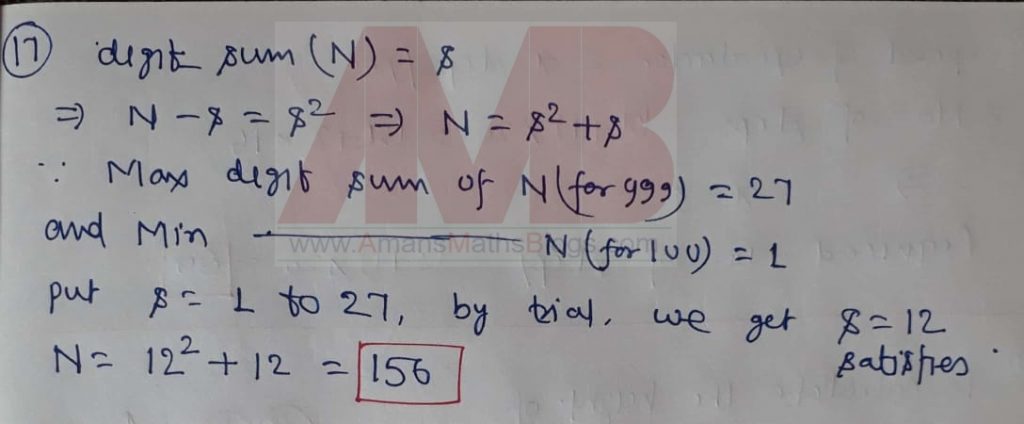NMTC 2019 Junior Level Class 9 & 10

NMTC 2019 Question Papers With Solutions Junior Level Class 9 and 10 is the exam conducted by AMTI. It was scheduled on 31 August 2019 at 2 PM to 4 PM.

Read: NMTC 2019 Notification

NMTC 2019 Junior Level Question Paper

NMTC 2019 Junior Level exam was conducted on 31 August 2019.

NMTC 2019 Junior Level Answer Keys

NMTC 2019 Junior Level
Answer Keys
Ques No	Ans Key	Ques No	Ans Key	Ques No	Ans Key	Ques No	Ans Key
1	D	9	B	17	156	25	89
2	D	10	D	18	16	26	97
3	B	11	D	19	80	27	25
4	C	12	C	20	Bonus	28	122
5	B	13	D	21	8/9	29	12
6	D	14	A	22	6	30	61
7	D	15	C	23	127
8	B	16	435	24	20

NMTC 2019 Junior Level Solutions

Part A: Instruction:

Only One of the choices A, B, C, D is correct. For each correct response, you get 1 mark. For each incorrect response, you lose 1/2 mark.

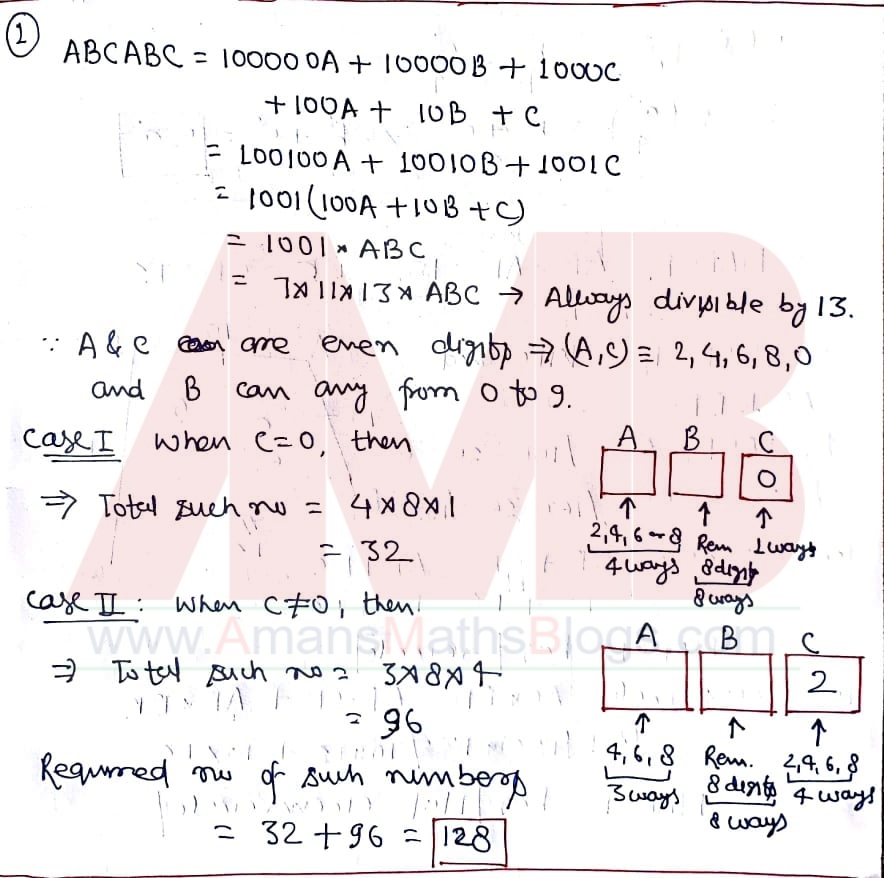
NMTC 2019 Question Papers With Solutions Junior Level Ques No 1:

The number of 6 digit numbers of the form “ABCABC”, which are divisible by 13, where A, B and C are distinct digits A and C being even digits is

Options:

A. 200

B. 250

C. 160

D. 128

Solution:

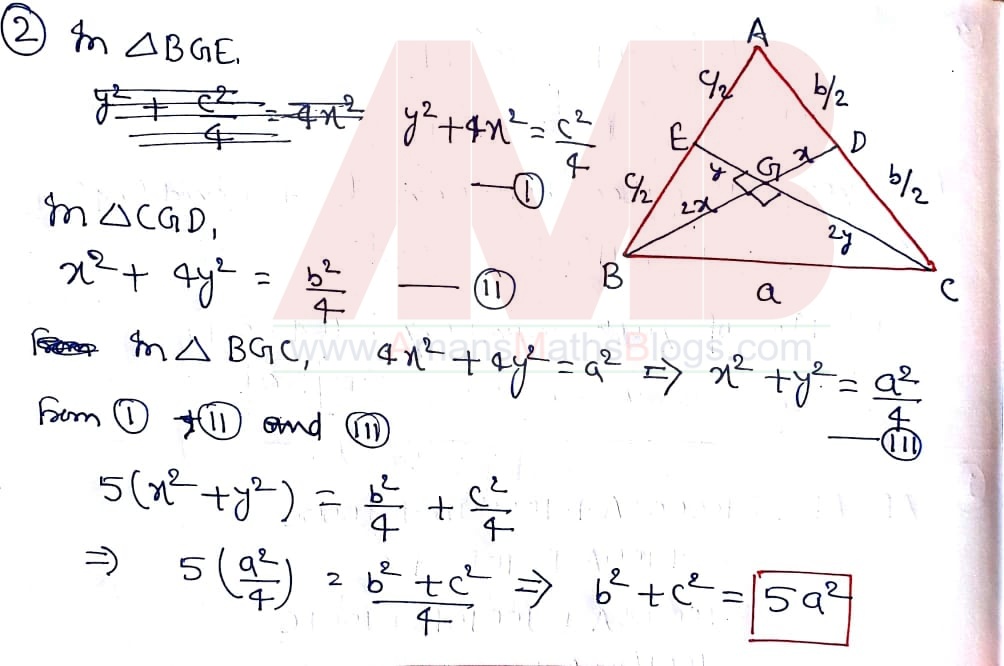
NMTC 2019 Question Papers With Solutions Junior Level Ques No 2:

In a triangle ABC, the medians through B and C are perpendicular. Then b² + c² is equal to

Options:

A. 2a²

B. 3a²

C. 4a²

D. 5a²

Solution:

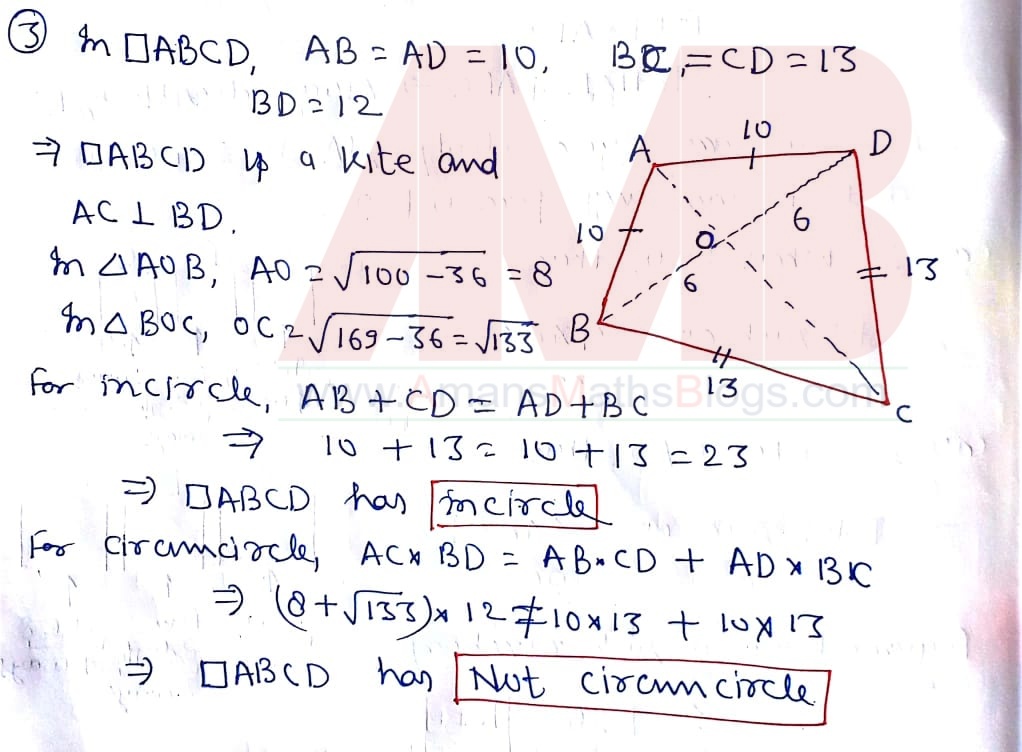
NMTC 2019 Question Papers With Solutions Junior Level Ques No 3:

In a quadrilateral ABCD, AB = AD = 10, BD = 12, CB = CD = 13. Then

Options:

A. ABCD is cyclic quadrilateral

B. ABCD has an in-circle

C. ABCD has both circumcircle and incircle

D. It has neither a circumcircle nor an incircle

Solution:

NMTC 2019 Question Papers With Solutions Junior Level Ques No 4:

Given three cubes with integer side lengths, if the sum of the surface areas of the three cubes is 498 sq. cm, then the sum of the volumes of the cubes in all possible solutions is

Options:

A. 731

B. 495

C. 1226

D. None of these

Solution:

NMTC 2019 Question Papers With Solutions Junior Level Ques No 5:

In a rhombus of side length 5, the length of one of the diagonals is at least 6, and the length of the other diagonal is at most 6. What is the maximum value of the sum of the diagonals?

Options:

A. 10√2

B. 14

C. 5√6

D. 12

Solution:

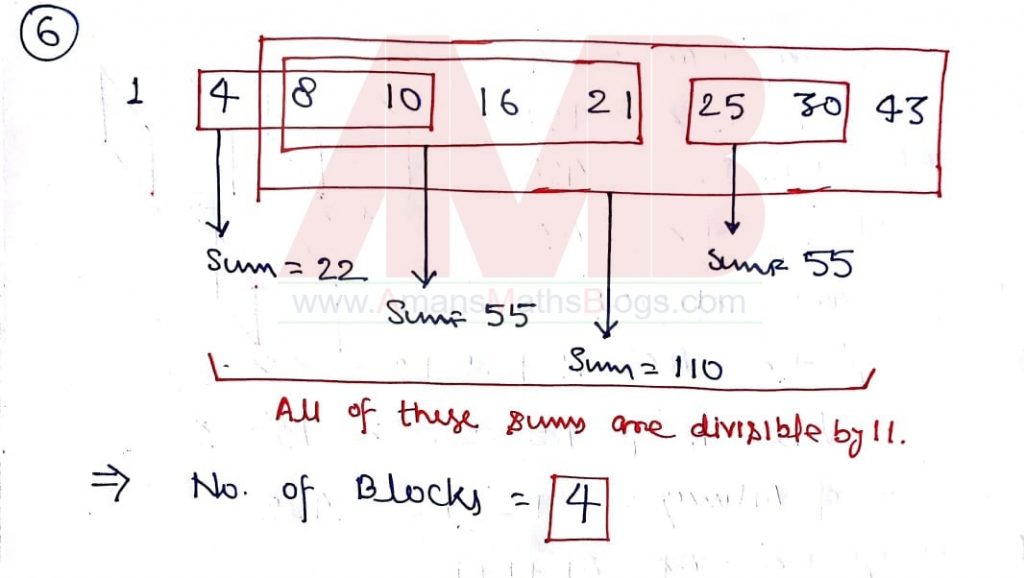
NMTC 2019 Question Papers With Solutions Junior Level Ques No 6:

In a sequence 1, 4, 8, 10, 16, 21, 25, 30 and 43, then the number of blocks of consecutive terms whose sums are divisible by 11 is

Options:

A. Only One

B. Exactly Two

C. Exactly Three

D. Exactly Four

Solution:

NMTC 2019 Question Papers With Solutions Junior Level Ques No 7:

Let A = {1, 2, 3, 4, …, 17}. For every nonempty subset B of A find he product of the reciprocals of the members of B. The sum of all such product is

Options:

A. 153/171

B. 153/LCM(1, 2, 3, 4, …, 17)

C. 18

D. 17

Solution:

NMTC 2019 Question Papers With Solutions Junior Level Ques No 8:

The remainder of f(x) = x¹⁰⁰ + x⁵⁰ + x¹⁰ + x² – 6 when divided by x² – 1 is

Options:

A. x + 1

B. -2

C. 0

D. 2

Solution:

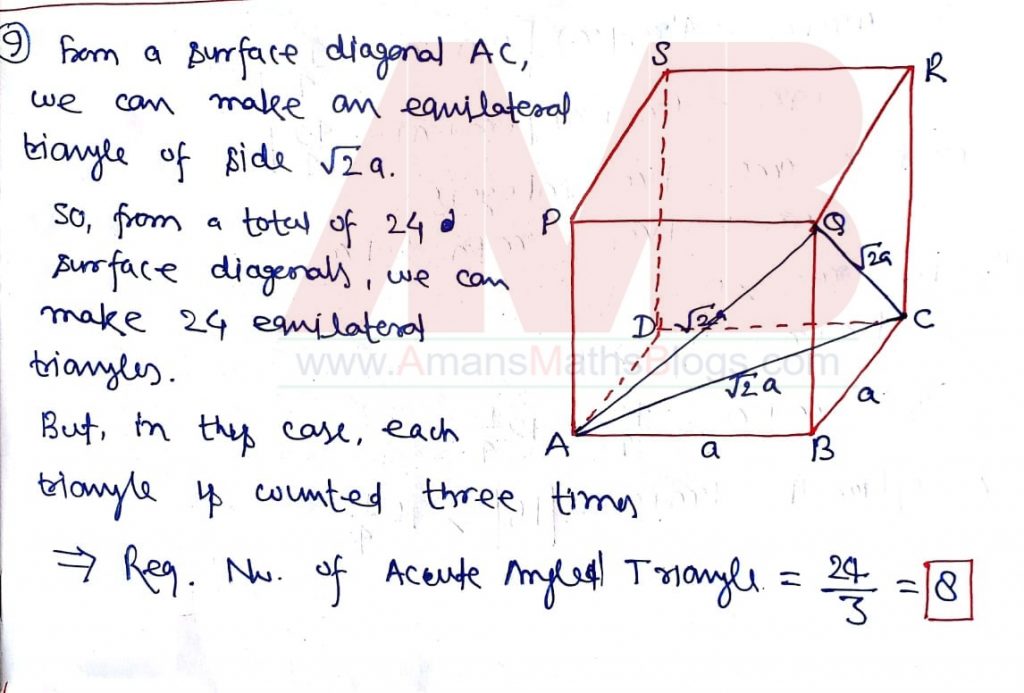
NMTC 2019 Question Papers With Solutions Junior Level Ques No 9:

The number of acute angled triangles whose vertices are chosen from the vertices of rectangular box is 

Options:

A. 6

B. 8

C. 12

D. 24

Solution:

NMTC 2019 Question Papers With Solutions Junior Level Ques No 10:

In the subtraction below, what is the sum of the digits in the result?

111…111(100 digits) – 222….222(50 digits)

Options:

A. 375

B. 420

C. 429

D. 450

Solution:

NMTC 2019 Question Papers With Solutions Junior Level Ques No 11:

If m and n are positive integers such that (m + n) / (m² + mn + n²) = 4/49, then the value of (m + n) is

Options:

A. 4

B. 8

C. 12

D. 16

Solution:

NMTC 2019 Question Papers With Solutions Junior Level Ques No 12:

Given a sheet of 16 stamps as shown, the number of ways of choosing three connected stamps (two adjacent stamps must have an edge in common) is

Options:

A. 40

B. 41

C. 42

D. 44

Solution:

NMTC 2019 Question Papers With Solutions Junior Level Ques No 13:

In an election 320 votes were cast for five candidates. The winner’s margins over the other four candidates were 9, 13, 18 and 25. The lowest number of votes received by a candidate was 

Options:

A. 49

B. 50

C. 51

D. 52

Solution:

NMTC 2019 Question Papers With Solutions Junior Level Ques No 14:

A competition has 25 questions and is marked as follows:

(a) Five marks are awarded for each correct answer to Question 1 to 15

(b) Six marks are awarded for each correct answer to Question 16 to 25

(c) Each incorrect answer to Questions 16 to 20 loses 1 mark

(d) Each incorrect answer to Questions 21 to 25 loses 2 marks

Which of the following scores is impossible to achieve?

Options:

A. 126

B. 127

C. 128

D. 129

Solution:

NMTC 2019 Question Papers With Solutions Junior Level Ques No 15:

A, M, T, I are positive integers such that A + M + T + I = 10. The maximum possible value of (A x M x T x I) + (A x M x T) + (A x M x I) + (A x T x I) + (M x T x I) + (A x M) + (A x T) + (A x I) + (M x T) + (M x I) + (T x I) is

Options:

A. 109

B. 121

C. 133

D. 144

Solution:

Part B: Instruction:

Write the correct answer in the space provided in the responsive sheet. For each correct response, you get 1 mark. For each incorrect response, you lose 1/4 mark.

NMTC 2019 Question Paper With Solutions Junior Level Ques No 16:

The three digit number XYZ when divided by 8, gives as quotient the two digit number ZX and remainder Y. The number XYZ is ______.

Solution:

NMTC 2019 Question Paper With Solutions Junior Level Ques No 17:

The digit sum of any number is the sum of the digits. N is a 3 digit number. When the digit sum of N is subtracted from N, we obtain the square of the digit sum of the N. The number N is _______.

Solution:

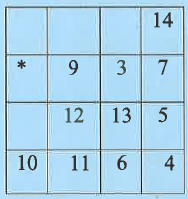
NMTC 2019 Question Paper With Solutions Junior Level Ques No 18:

A 4 x 4 anti magic square is an arrangement of the numbers 1 to 16 in a square so that the totals of each of the four rows, four columns and the two diagonals are ten consecutive numbers in some order. The diagram shows an incomplete anti magic square. When it is completed, the number in the position of * is

Solution:

NMTC 2019 Question Paper With Solutions Junior Level Ques No 19:

An escalator moves up to a constant rate. john walks up the escalator at the rate of one step per second and reaches the top in twenty seconds. The next day John’s rate was two steps per second, and he reached the top in sixteen seconds. The number of steps in the escalator is _____.

Solution:

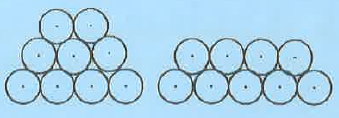
NMTC 2019 Question Paper With Solutions Junior Level Ques No 20:

In a stack of coins, each row has exactly one coin less than the row below. If we have nine coins, two such towers are possible. Of these, the tower on the left is the tallest. If you have 2015 coins, the height of the tallest tower is ______.

Solution:

NMTC 2019 Question Paper With Solutions Junior Level Ques No 21:

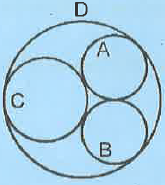
Circles A, B and C are exactly tangent to each other and internally tangent to circle D. Circles A and B are congruent. Circle C has radius 1 unit and passes through the centre of circle D. Then the radius of circle B is _____ units.

Solution:

NMTC 2019 Question Paper With Solutions Junior Level Ques No 22:

The number of different integers x that satisfy the equation (x² – 5x + 5)^{(x2 – 11x + 30)} = 1 is ____.

Solution:

NMTC 2019 Question Paper With Solutions Junior Level Ques No 23:

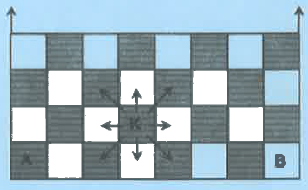
In a single move a King K is allowed to move to any of the squares touching the square it is on, including diagonals as indicated in the figure. The number of different paths using exactly seven moves to go from A to B is _____.

Solution:

NMTC 2019 Question Paper With Solutions Junior Level Ques No 24:

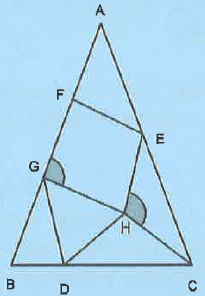
In a triangle ABC as shown below, AB = AC; F is a point on AB and E a point on AC such that AF = EF. H is a point in the interior of triangle ABC, D is a point on BC and G is point on AB such that EH = CH = DH = GH = DG = BG. Also ∠CHE = ∠HGF. The measure of ∠BAC in degrees is ______. 

Solution:

NMTC 2019 Question Paper With Solutions Junior Level Ques No 25:

Let x and y be real numbers satisfying x⁴y⁵ + y⁴x⁵ = 810 and x³y⁶ + y³x⁶ = 945. Then the value of 2x³ + x³y³ + 2y³ is _______.

Solution:

NMTC 2019 Question Paper With Solutions Junior Level Ques No 26:

The least odd prime factor of 2019⁸ + 1 is ______.

Solution:

NMTC 2019 Question Paper With Solutions Junior Level Ques No 27:

Let a, b, c be positive integers each less than 50, such that a² – b² = 100c. The number of such triplets (a, b, c) is ______.

Solution:

NMTC 2019 Question Paper With Solutions Junior Level Ques No 28:

The number of non-negative integers which can be written in the form,

where b_i ∈ {-1, 0, 1} for 0 ≤ i ≤ 4 is _____.

Solution:

NMTC 2019 Question Paper With Solutions Junior Level Ques No 29:

{ak} is a sequence of integers, with a₁ = -2 and a_m+n = a_m + a_n + mn, for all positive integers m, n. Then the value of a₈ = _______.

Solution:

NMTC 2019 Question Paper With Solutions Junior Level Ques No 30:

The coefficient of x⁹⁰ in (1 + x + x² + x³ + … + x⁶⁰)(1 + x + x² + … + x¹²⁰) is equal to _____. 

Solution:

 

 

 

 

 

 

 

math blogsnmtcnmtc 2019nmtc 2019 answer keysnmtc junior levelnmtc previous questionsnmtc previous year answersnmtc questions papersnmtc solved papersprevious year question papers