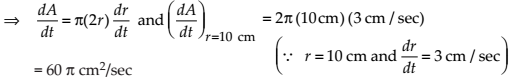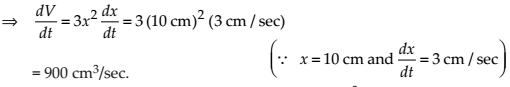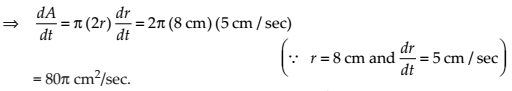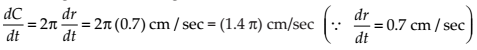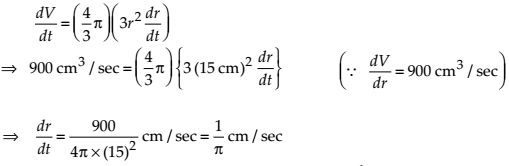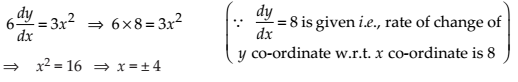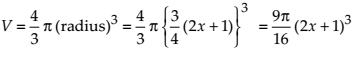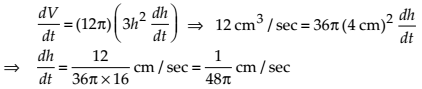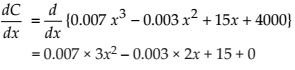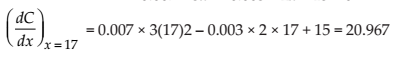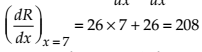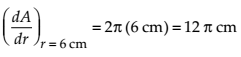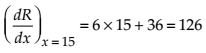NCERT Solutions for Class 12 Maths Application of Derivatives

Hi Students, Welcome to Amans Maths Blogs (AMB). In this post, you will get the NCERT Solutions for Class 12 Maths Application of Derivative Exercise 6.1.

CBSE Class 12^th is an important school class in your life as you take some serious decision about your career. And out of all subjects, Maths is an important and core subjects. So CBSE NCERT Solutions for Class 12^th Maths is major role in your exam preparation as it has detailed chapter wise solutions for all exercise. This NCERT Solutions can be downloaded in PDF file. The downloading link is given at last.

NCERT Solutions for class 12 is highly recommended by the experienced teacher for students who are going to appear in CBSE Class 12 and JEE Mains and Advanced and NEET level exams. Here You will get NCERT Solutions for Class 12 Maths Application of Derivative Exercise 6.1 of all questions given in NCERT textbooks of class 12 in details with step by step process.

The PDF books of NCERT Solutions for Class 12 are the first step towards the learning and understanding the each sections of Maths, Physics, Chemistry, Biology as it all help in engineering medical entrance exams. To solve it, you just need to click on download links of NCERT solutions for class 12.

NCERT Solutions for Class 12 Maths are not only the solutions of Maths exercise but it builds your foundation of other important subjects. Getting knowledge of depth concept of CBSE Class 12^th Maths like Algebra, Calculus, Trigonometry, Coordinate Geometry help you to understand the concept of Physics and Physical Chemistry.

As we know that all the schools affiliated from CBSE follow the NCERT books for all subjects. You can check the CBSE NCERT Syllabus. Thus, NCERT Solutions helps the students to solve the exercise questions as given in NCERT Books. 

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 1.

Find the rate of change of the area of a circle with respect to its radius r when (a) r = 3cm, (b) r = 4cm

NCERT Solutions:

Given that the radius of circle is r, then its area is A = πr².

On differentiating with respect to r, we get

dA/dr = 2πr

Thus,

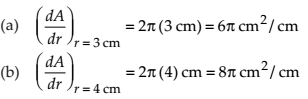
NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 2.

The volume of a cube is increasing at the rate of 8 cm³/s. How fast is the surface area increasing when the length of an edge is 12 cm?

NCERT Solutions:

Let at any instant time t, the side of the cube is x, then its volume is V = x³ and its surface area is S = 6x².

Then, On differentiating V = x³ and S = 6x² with respect to t, we get 

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 3.

The radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.

NCERT Solutions:

Let at any instant time t, the radius of the circle is r, then its area is A = πr². 

On differentiating with respect to r, we get

Thus, the rate of increase of area of the circle is 60π cm²/sec.

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 4.

An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long?

NCERT Solutions:

Let at any instant time t, the edge of the cube is x, then its volume is V = x³.

Then, On differentiating V = x³ with respect to t, we get 

Thus, the rate of increase of volume of the cube is 900 cm³/sec.

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 5.

A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm/s. At the instant when the radius of the circular wave is 8 cm, how fast is the enclosed area increasing?

NCERT Solutions:

Let at any instant time t, the radius of the circular wave is r, then its area is A = πr².

Then, On differentiating A = πr² with respect to t, we get 

Thus, the rate of increase of enclosed area is 80π cm²/sec.

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 6.

The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?

NCERT Solutions:

Let at any instant time t, the radius of the circular wave is r, then its circumference is C = 2πr.

Then, On differentiating C = 2πr with respect to t, we get 

Thus, the rate of increase of the circumference is 1.4π cm/sec.

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 7.

The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8cm and y = 6cm, find the rates of change of (a) the perimeter, and (b) the area of the rectangle.

NCERT Solutions:

Let at any instant time t, the length and the breadth of the rectangle is x and y respectively.

Then, we have

(a) The perimeter of the rectangle is P = 2(x + y)

Then, On differentiating P = 2(x + y) with respect to t, we get 

Thus, the perimeter of the rectangle is decreasing at the rate of 2 cm/min.

(b) The area of the rectangle is A = xy.

Then, On differentiating A = xy with respect to t, we get 

Thus, the area of the rectangle is increasing at the rate of 2 cm²/min.

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 8.

A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15 cm.

NCERT Solutions:

Let at any instant time t, the radius of the balloon is r, then its volume is V = 4/3 πr³.

Then, On differentiating V = 4/3 πr³ with respect to t, we get 

Thus, the rate of increase of the radius of the balloon is 1/π cm/sec.

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 9.

A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the later is 10 cm.

NCERT Solutions:

Let at any instant time t, the radius of the balloon is r, then its volume is V = 4/3 πr³.

Then, On differentiating V = 4/3 πr³ with respect to t, we get 

Thus, the rate of increase of the volume of the balloon is 400π cm²/cm.

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 10.

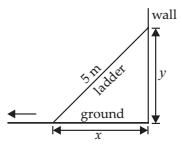
A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall ?

NCERT Solutions:

Let the foot of the ladder is at a distance x from the wall and the top is a height of y at a time t.

Then, 25 m² = x² + y².

Then, On differentiating with respect to t, we get 

Given that dx/dt = 0.02 m/sec and x = 3 , then y = 4.

Thus, we get

Thus, the rate of decrease of the height of the wall is 16/600 m/sec = 8/3 cm/sec.

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 11.

A particle moves along the curve 6y = x³ +2. Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate.

NCERT Solutions:

Given that 6y = x³ + 2    …(i)

Then, on differentiating with respect to x, we get 

Now, when x = 4, then using (i), y = 11 and when x = -4, then using (i), y = -31/3.

Thus, the points are (4, 11) and (-4, -31/3).

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 12.

The radius of an air bubble is increasing at the rate of 1/2 cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?

NCERT Solutions:

Let at any instant time t, the radius of the bubble is r, then its volume is V = 4/3 πr³.

Then, On differentiating V = 4/3 πr³ with respect to t, we get 

Thus, the rate of increase of the volume of the bubble is 2π cm³/sec.

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 13.

A balloon, which always remains spherical, has a variable diameter (3/2)(2x + 1). Find the rate of change of its volume with respect to x.

NCERT Solutions:

Since the diameter of the balloon is d = (3/2)(2x + 1).

Then, the radius of the balloon is r = d/2 = (3/2)(2x + 1).

And its volume is 

Then, On differentiating with respect to x, we get

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 14.

Sand is pouring from a pipe at the rate of 12 cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?

NCERT Solutions:

Let the radius of the base of the cone is r, its height is h and the volume is V. Then,

Then, On differentiating with respect to t, we get 

Thus, the rate of the increase of the height of the sand cone is 1/48π cm/sec.

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 15.

The total cost C(x) in Rupees associated with the production of x units of an item is given by
C(x) = 0.007x³ – 0.003x² + 15x + 4000. Find the marginal cost when 17 units are produced.

NCERT Solutions:

Given that C(x) = 0.007x³ – 0.003x² + 15x + 4000.

Then, On differentiating with respect to x, we get 

Thus, the marginal cost (when x = 17) is

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 16.

The total revenue in Rupees received from the sale of x units of a product is given by
R(x) = 13x² + 26x + 15. Find the marginal revenue when x = 7.

NCERT Solutions:

Given that R(x) = 13x² + 26x + 15.

Then, On differentiating with respect to x, we get 

Thus, the marginal revenue (when x = 7) is

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 17.

The rate of change of the area of a circle with respect to its radius r at r = 6 cm is
(A) 10π (B) 12π (C) 8π (D) 11π

NCERT Solutions:

Let the radius of the circle is r, then its area is A = πr². 

On differentiating with respect to r, we get

Thus, the rate of increase of area of the circle is

NCERT Solutions for Class 12 Maths Application of Derivatives Exercise 6.1: Ques No 18.

The total revenue in Rupees received from the sale of x units of a product is given by
R(x) = 3x² + 36x + 5. The marginal revenue, when x = 15 is (A) 116 (B) 96 (C) 90 (D) 126

NCERT Solutions:

Given that R(x) = 3x² + 36x + 5.

Then, On differentiating with respect to x, we get 

Thus, the marginal revenue (when x = 15) is

 

 

application of derivativesapplication of derivatives formulaapplication of derivatives in real lifeapplication of derivatives pdfapplication of partial derivativesclass 12 maths ncert solutionsncert solutionsncert solutions class 12ncert solutions class 12 mathsncert solutions class 12th mathsncert solutions class 12th maths pdfncert solutions for class 12ncert solutions for class 12 maths