NCERT Solutions for Class 12 Maths Linear Programming
Hi Students, Welcome to Amans Maths Blogs (AMB). In this post, you will get the NCERT Solutions for Class 12 Maths Linear Programming Exercise 12.1.
As we know that all the schools affiliated from CBSE follow the NCERT books for all subjects. You can check the CBSE NCERT Syllabus. Thus, NCERT Solutions helps the students to solve the exercise questions as given in NCERT Books.
NCERT Solutions for class 12 is highly recommended by the experienced teacher for students who are going to appear in CBSE Class 12 and JEE Mains and Advanced and NEET level exams. Here You will get NCERT Solutions for Class 12 Maths Linear Programming Exercise 12.1 of all questions given in NCERT textbooks of class 12 in details with step by step process.
NCERT Solutions for Class 12 Maths Linear Programming
Solve the following Linear Programming Problems graphically:
NCERT Solutions for Class 12 Maths Linear Programming Exercise 12.1 Ques No 1.
Maximise: Z = 3x + 4y
Subject to the Constraints : x + y ≤ 4, x ≥ 0, y ≥ 0.
NCERT Solutions:
Given Constraints : x + y ≤ 4, x ≥ 0, y ≥ 0.
Now, let the line l : x + y = 4 and draw its graph and also apply the given constraints. The shaded region in the given figure is the feasible region determined by the system of given constraints.
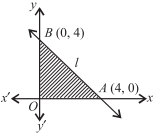
Since the feasible region is OAB is bounded, we need to use Corner Point Method to maximize Z = 3x + 4y.
Now, on solving the equations x + y = 4, x = 0 and y = 0, we get that the coordinate of O, A and B are (0, 0), (4, 0) and (0, 4) respectively.
Thus, maximum value of Z is 16 at the point (0, 4).
NCERT Solutions for Class 12 Maths Linear Programming Exercise 12.1 Ques No 2.
Minimise Z = – 3x + 4 y
subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0.
NCERT Solutions:
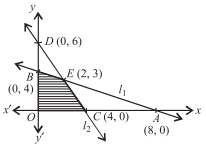
Given Constraints : x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0.
Now, let the line l1 : x + 2y = 8 and l2 : 3x + 2y = 12 and draw its graph and also apply the given constraints. The shaded region in the given figure is the feasible region determined by the system of given constraints.
Since the feasible region is OBCE is bounded, we need to use Corner Point Method to minimize Z = – 3x + 4 y.
Now, on solving the equations of lines, we get that the coordinate of O, B, E and C are (0, 0), (0, 4), (2, 3) and (4, 0) respectively.
Thus, minimum value of Z is –12 at the point (4, 0).
NCERT Solutions for Class 12 Maths Linear Programming Exercise 12.1 Ques No 3.
Maximise Z = 5x + 3y
subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0.
NCERT Solutions:
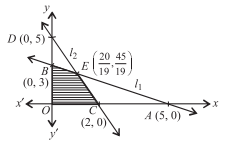
Given Constraints : 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0.
Now, let the line l1 : 3x + 5y = 15 and l2 : 5x + 2y ≤ 10 and draw its graph and also apply the given constraints. The shaded region in the given figure is the feasible region determined by the system of given constraints.
Since the feasible region is OBCE is bounded, we need to use Corner Point Method to minimize Z = 5x + 3y.
Now, on solving the equations of lines, we get that the coordinate of O, B, E and C are (0, 0), (0, 3), (20/19, 45/19) and (2, 0) respectively.
Thus, maximum value of Z is 235/19 at the point (20/19, 45/19).
NCERT Solutions for Class 12 Maths Linear Programming Exercise 12.1 Ques No 4.
Minimise Z = 3x + 5y
subject to : x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.
NCERT Solutions:
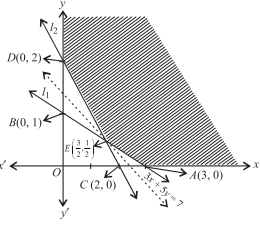
Given Constraints : x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.
Now, let the line l1 : x + 3y = 3 and l2 : x + y = 2 and draw its graph and also apply the given constraints. The shaded region in the given figure is the feasible region determined by the system of given constraints.
Since the feasible region is unbounded, we need to use Corner Point Method to minimize Z = 3x + 5y.
Now, on solving the equations of lines, we get that the coordinate of A, E and D are (3, 0), (3/2, 1/2), and (0, 2) respectively.
Thus, minimum value of Z is 7 at the point (3/2, 1/2).
NCERT Solutions for Class 12 Maths Linear Programming Exercise 12.1 Ques No 5.
Maximise Z = 3x + 2y
subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
NCERT Solutions:
Given Constraints : x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Now, let the line l1 : x + 2y = 10 and l2 : 3x + y = 15 and draw its graph and also apply the given constraints. The shaded region in the given figure is the feasible region determined by the system of given constraints.
Since the feasible region is bounded, we need to use Corner Point Method to maximize Z = 3x + 2y.
Now, on solving the equations of lines, we get that the coordinate of O, C, E and B are (0, 0), (5, 0), (4, 3) and (0, 5) respectively.
Thus, maximum value of Z is 18 at the point (4, 3).
NCERT Solutions for Class 12 Maths Linear Programming Exercise 12.1 Ques No 6.
Minimize Z = x + 2y
subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
NCERT Solutions:
Given Constraints : 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Now, let the line l1 : 2x + y = 3 and l2 : x + 2y = 6 and draw its graph and also apply the given constraints. The shaded region in the given figure is the feasible region determined by the system of given constraints.
Since the feasible region is unbounded, we need to use Corner Point Method to maximize Z = x + 2y.
Now, on solving the equations of lines, we get that the coordinate of B and C are (0, 3) and (6, 0) respectively.
Thus, minimum value of Z is 6 at the point (6, 0) and (0, 3).
NCERT Solutions for Class 12 Maths Linear Programming Exercise 12.1 Ques No 7.
Minimise and Maximise Z = 5x + 10 y
Subject to x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0.
Show that the maximum of Z occurs at two points.
NCERT Solutions:
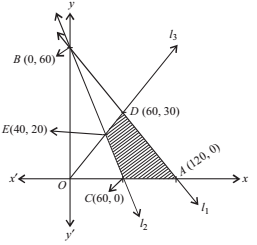
Given Constraints : x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0.
Now, let the line l1 : x + 2y = 120, l2 : x + y = 60 and l3 : x – 2y = 0 and draw its graph and also apply the given constraints. The shaded region in the given figure is the feasible region determined by the system of given constraints.
Since the feasible region CADE is bounded, we need to use Corner Point Method to minimize and maximize Z = 5x + 10y.
Now, on solving the equations of lines, we get that the coordinates as C(60, 0), A(120, 0), D(60, 30), E(40, 20).
Thus, the minimum of Z is 300 at C(60, 0) and maximum of Z is 600 at A(120, 0) and D(60, 30).
NCERT Solutions for Class 12 Maths Linear Programming Exercise 12.1 Ques No 8.
Minimise and Maximise Z = x + 2y
Subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
Show that the minimum of Z occurs at two points.
NCERT Solutions:
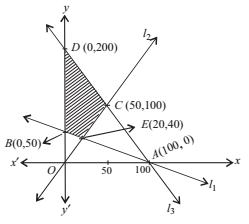
Given Constraints : x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
Now, let the line l1 : x + 2y = 100, l2 : 2x – y = 0 and l3 : 2x + y = 200 and draw its graph and also apply the given constraints. The shaded region in the given figure is the feasible region determined by the system of given constraints.
Since the feasible region BDCE is bounded, we need to use Corner Point Method to minimize and maximize Z = x + 2y.
Now, on solving the equations of lines, we get that the coordinates as B(0, 50), D(0, 200), C(50, 100), E(20, 40).
Thus, the maximum of Z is 400 at D(0, 200) and minimum of Z is 100 at B(0, 50) and E(20, 40).
NCERT Solutions for Class 12 Maths Linear Programming Exercise 12.1 Ques No 9.
Maximize Z = – x + 2y,
Subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
NCERT Solutions:
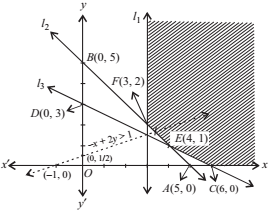
Given Constraints : x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
Now, let the line l1 : x = 3, l2 : x + y = 5 and l3 : x + 2y = 6 and draw its graph and also apply the given constraints. The shaded region in the given figure is the feasible region determined by the system of given constraints.
Since the feasible region is unbounded, we need to use Corner Point Method to maximize Z = – x + 2y.
Now, on solving the equations of lines, we get that the coordinates as C(6, 0), E(4, 1), and F(3, 2).
From the table, we see that the maximum value of Z is 1 at F(3, 2). But the feasible region is unbounded, therefore, we draw the graph of the inequality – x + 2y > 1. Since half plane represented by – x + 2y > 1 has points common with the feasible region.
Thus, the maximum value of Z cannot be 1. hence, Z has no maximum value.
NCERT Solutions for Class 12 Maths Linear Programming Exercise 12.1 Ques No 10.
Maximise Z = x + y,
Subject to the constraints: x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
NCERT Solutions:
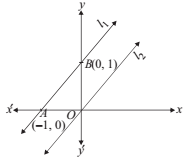
Given Constraints : x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
Now, let the line l1 : x – y = –1, and l3 : –x + y = 0 and draw its graph and also apply the given constraints.
Since there is no common region, hence there is no feasible region.
Therefore, there is no maximum value of Z.