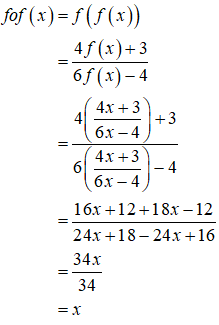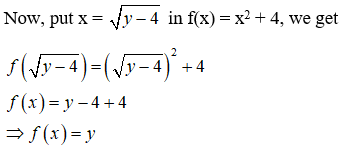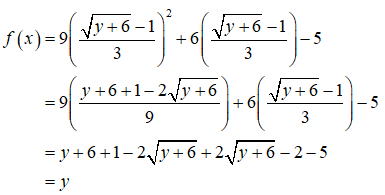NCERT Solutions for Class 12 Maths Relations and Functions

Hi Students, Welcome to Amans Maths Blogs (AMB). In this post, you will get the NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3. This NCERT Solutions can be downloaded in PDF file. The downloading link is given at last.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 1. 

Let f : {1, 3, 4} → {1, 2, 5} and g : {1, 2, 5} → {1, 3} be given by f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}. Write down gof.

NCERT Solutions:

Given that f : {1, 3, 4} → {1, 2, 5} and g : {1, 2, 5} → {1, 3} where f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}.

We need to find gof(x) = g[f(x)].

Put x = 1, we get gof(1) = g[f(1)] = g[2] = 3

Put x = 3, we get gof(3) = g[f(3)] = g[5] = 1

Put x = 4, we get gof(4) = g[f(4)] = g[1] = 3

Thus, gof = {(1, 3), (3, 4), (4, 3)}

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 2. 

Let f, g and h be functions from R to R. Show that (f + g) oh = foh + goh and (f . g) oh = (foh) . (goh)

NCERT Solutions:

Proof of (f + g) oh = foh + goh

LHS

= [(f + g)oh](x)

= (f + g)[h(x)]

= f [h(x)] + g[h(x)]

= (foh)(x) + (goh)(x)

= {(foh) + (goh)}(x)

= RHS

Thus, we get {(f + g)oh}(x) = {(foh)(x) + (goh)}(x) for all x ∈R.

Proof of (f.g) oh = (foh) . (goh)

LHS

= [(f.g)oh](x)

= (f.g)[h(x)]

= f[h(x)] . g[h(x)]

= (foh)(x) . (goh)(x)

= {(foh).(goh)}(x)

= RHS

Thus, we get [(f.g)oh](x) = {(foh).(goh)}(x) for all x ∈R.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 3. 

Find gof and fog, if

(i) f(x) = | x | and g(x) = | 5x – 2 |

NCERT Solutions:

Given that ?(x) = |x| and g(x) = |5x – 2|

Thus, we get gof(x) = g(f(x)) = |5(f(x)) – 2| = | 5| x | – 2|

And, fog(x) = f(g(x)) = | g(x) | = || 5x – 2|| = | 5x – 2|

(ii) f(x) = 8x³ and g(x) = x^1/3

NCERT Solutions:

Given that f(x) = 8x³ and g(x) = x^1/3

Thus, we get

gof(x) = g(f(x)) = g(x3) = (8x³)^1/3 = 2x

And, fog(x) = f(g(x)) = f(x^1/3) = 8(x^1/3)3 = 8x

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 4. 

If f(x) = (4x + 3)/(6x – 4), x ≠ 2/3, show that fof(x) = x for all x ≠ 2/3. What is the inverse of f ?

NCERT Solutions:

Given that f(x) = (4x + 3)/(6x – 4), x ≠ 2/3. Thus, we get

Thus, fof(x) = x for all x ≠ 2/3.

We get that fof(x) = I_x

Hence, the given function f is invertible and the inverse of f is f itself.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 5. 

State with reason whether following functions have inverse

(i) f : {1, 2, 3, 4} → {10} with f = {(1, 10), (2, 10), (3, 10), (4, 10)}

NCERT Solutions:

Given that f : {1, 2, 3, 4} → {10} with f = {(1, 10), (2, 10), (3, 10), (4, 10)}

Since f(1) = f(2) = f(3) = f(4) = 10, the given function is not one-one.

Hence, the given function has not inverse.

(ii) g : {5, 6, 7, 8} → {1, 2, 3, 4} with g = {(5, 4), (6, 3), (7, 4), (8, 2)}

NCERT Solutions:

Given that g : {5, 6, 7, 8} → {1, 2, 3, 4} with g = {(5, 4), (6, 3), (7, 4), (8, 2)}

Since g(5) = g(7) = 4, the given function is not one-one.

Hence, the given function has not inverse.

(iii) h : {2, 3, 4, 5} → {7, 9, 11, 13} with h = {(2, 7), (3, 9), (4, 11), (5, 13)}

NCERT Solutions:

Given that h : {2, 3, 4, 5} → {7, 9, 11, 13} with h = {(2, 7), (3, 9), (4, 11), (5, 13)}

Since h = {(2, 7), (3, 9), (4, 11), (5, 13)}, the given function is one-one.

Since every element y of the set {7, 9, 11, 13} there exists an element x in the set {2, 3, 4, 5} such that h(x) = y, the given function is on-to function.

Thus, the given function is one-one on-to function. It has inverse function.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 6. 

Show that f : [–1, 1] → R, given by f (x) = x/(x + 2) is one-one. Find the inverse of the function f : [–1, 1] → Range f.

NCERT Solutions:

Given that f : [–1, 1] → R, given by f (x) = x/(x + 2).

For one-one, f(x) = f(y)

⇒ x/(x + 2) = y/(y + 2)

⇒ x(y + 2) = y(x + 2)

⇒ xy + 2x = xy + 2y

⇒ 2x = 2y

⇒ x = y

Thus, the given function is one-one function.

Since f : [–1, 1] → Range f, the given function is on-to function.

Therefore, the given function f : [–1, 1] → Range is one-one on-to function and hence its inverse exists.

Let g: Range f → [−1, 1] be the inverse of f. Let y be an arbitrary element of range f. Since f: [−1, 1] → Range f is onto, we have y = f(x) for some x ∈ [−1, 1]

⇒ y = x/(x + 2)

⇒ xy + 2y = x

⇒ x(1 – y) = 2y

⇒ x = 2y/(1 – y) , y ≠ 1

Thus, f^–1(x) = 2x/(1 – x), x ≠ 1

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 7. 

Consider f : R → R given by f(x) = 4x + 3. Show that f is invertible. Find the inverse of f.

NCERT Solutions:

Given that f : R → R given by f(x) = 4x + 3

For one-one, f(x) = f(y)

⇒ 4x + 3 = 4y + 3

⇒ 4x = 4y

⇒ x = y

Thus, f is one-one function.

For on-to, let y = 4x + 3 ⇒ x = (y – 3)/4. Put x = (y – 3)/4  in f(x) = 4x + 3.

We get f(x) = 4(y – 3)/4 + 3 = y

Thus, the given function is on-to function.

Therefore, the given function has its inverse.

Since y = 4x + 3 ⇒ x = (y – 3)/4, then the inverse of the given function is

f^–1(x) = (x – 3)/4.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 8. 

Consider f : R⁺ → [4, ∞) given by f(x) = x² + 4. Show that f is invertible with the inverse f ^–1of f given by f^-1(y) = √(y – 4), where R⁺ is the set of all non-negative real numbers.

NCERT Solutions:

Given that f : R⁺ → [4, ∞) given by f(x) = x² + 4.

For one-one, f(x) = f(y)

⇒ x² + 4 = y² + 4

⇒ x² = y²

⇒ x = y    [x and y in R⁺]

Thus, f is one-one function.

For on-to,

For y ∈ [4, ∞), let y = x² + 4

⇒ ?² = ? − 4

⇒ x = √(y – 4) >= 0

Thus, the given function is on-to function.

Therefore, the given function is one-one on-to function and hence its inverse exists.

And, the inverse of the given function is f^-1(y) = √(y – 4).

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 9. 

Consider f : R⁺ → [– 5, ∞) given by f (x) = 9x² + 6x – 5. Show that f is invertible with

.

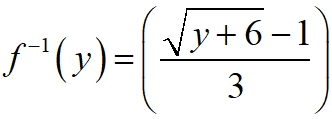
NCERT Solutions:

Given that f : R⁺ → [–5, ∞) given by f(x) = 9x² + 6x – 5.

For one-one, f(x) = f(y)

⇒ 9x² + 6x – 5 = 9y² + 6y – 5

⇒ 9(x² – y²) + 6(x – y) = 0

⇒ (x – y) [9(x – y) + 6] = 0

⇒ (x – y) = 0

⇒ x = y

Thus, f is one-one function.

For on-to function,

Let y = 9x² + 6x – 5

⇒ y = 9x² + 6x  + 1 – 6

⇒ y = (3x + 1)² – 6

⇒ (3x + 1)² = y + 6

⇒ (3x + 1) = √(y + 6)

⇒ 3x = √(y + 6) – 1

⇒ x = (√(y + 6) – 1) / 3

Now, put x = (√(y + 6) – 1) / 3 in f(x) = 9x² + 6x – 5, we get

Since f(x) = y, then the given function is on-to function.

Therefore, the given function is one-one and on-to function and hence its inverse function exists.

And, its inverse function is

.

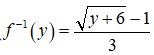
NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 10. 

Let f : X → Y be an invertible function. Show that f has unique inverse.

NCERT Solutions:

Given that f: X → Y be an invertible function.

Let f has two inverses g₁ and g₂.

Then, for all y ∈Y, we have

fog₁(y) = I_Y(y) = fog₂(y)

⇒ f(g₁ (y)) = f(g₂ (y))

⇒ g₁ (y) = g₂ (y) [as f is invertible ⇒ f is one – one]

⇒ ?1 = ?2 [as ? is one – one]

Hence, the given function f has a unique inverse.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 11. 

Consider f : {1, 2, 3} → {a, b, c} given by f(1) = a, f(2) = b and f(3) = c. Find f ^–1 and show that (f ^–1)^–1 = f.

NCERT Solutions:

Given that f : {1, 2, 3} → {a, b, c} given by f(1) = a, f(2) = b and f(3) = c.

Now,

(fog)(a) = f(g(a)) = f(1) = a

(fog)(b) = f(g(b)) = f(2) = b

(fog)(c) = f(g(c)) = f(3) = c

And,

(gof)(1) = g(f(1)) = f(a) = 1

(gof)(2) = g(f(2)) = f(b) = 2

(gof)(3) = g(f(3)) = f(c) = 3

Since gof = I_x and fog = I_y, where x = {1, 2, 3} and y= {a, b, c}.

Thus, the inverse of the given function f exists and f⁻¹ = g.

Therefore, f⁻¹ :{ a, b, c} → {1, 2, 3} is given by f⁻¹ (a) = 1, f⁻¹ (b) = 2, f^–1 (c) = 3.

Now, let h: {1, 2, 3} → {a, b, c} as h (1) = a, h (2) = b, h (3) = c. Then,

(goh)(1) = g(h(1)) = g(a) = 1

(goh)(2) = g(h(2)) = g(b) = 2

(goh)(3) = g(h(3)) = g(c) = 3

And,

(hog)(a) = h(g(a)) = h(1) = a

(hog)(b) = h(g(b)) = h(2) = b

(hog)(c) = h(g(c)) = h(3) = c

Thus, goh = I_x and hog = I_y, where x = {1, 2, 3} and y = {a, b, c}.

Thus, the inverse of g exists and g⁻¹ = h ⇒ (f⁻¹ )⁻¹ = h.

Since we have h = f. Hence, (f⁻¹)⁻¹ = f.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 12. 

Let f: X → Y be an invertible function. Show that the inverse of f ^–1 is f, i.e. (f ^–1)^–1 = f.

NCERT Solutions:

Given that f: X → Y be an invertible function.

Then, there exists a function g: Y → X such that gof = IX and fog = IY.

Since f−1 = g, then gof = I_x and fog = I_y

⇒ f⁻¹of = I_x and fof⁻¹ = I_y

Hence, f⁻¹: Y → X is invertible and f is the inverse of f⁻¹ i.e., (f⁻¹)⁻¹ = f.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 13. 

If f: R → R be given by f(x) = (3 – x³)^1/3 then fof(x) is

NCERT Solutions:

NCERT Solution for Class 12 Maths Relations and Functions Exercise 1.3: Ques No 14. 

NCERT Solutions:

class 12 maths ncert solutionsncert solutionsncert solutions class 12ncert solutions class 12 mathsncert solutions class 12th mathsncert solutions class 12th maths pdfncert solutions for class 12ncert solutions for class 12 mathsrelations and functionsrelations and functions class 12relations and functions class 12 ncert solutions