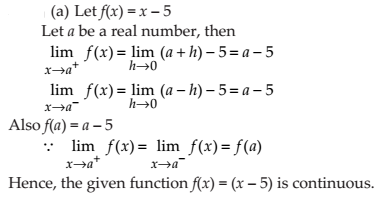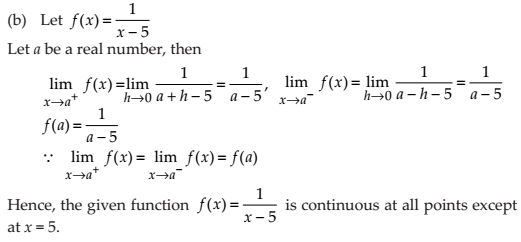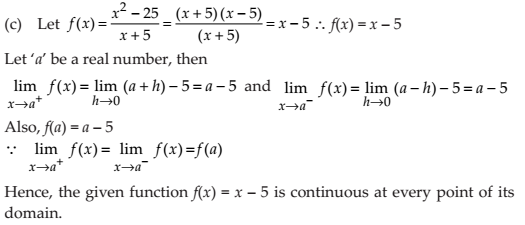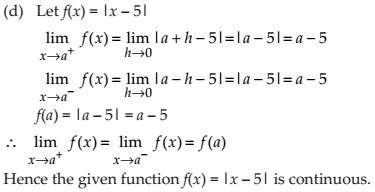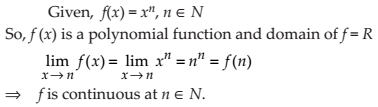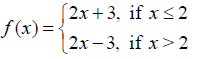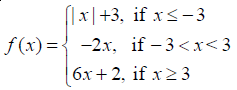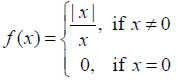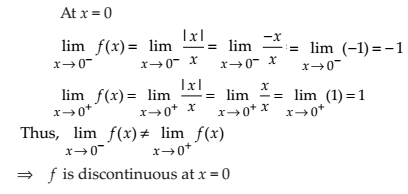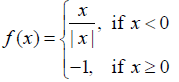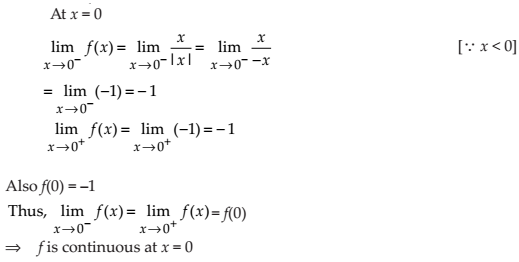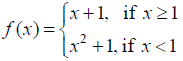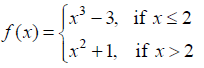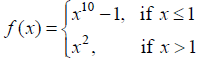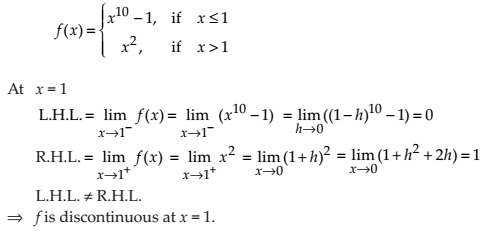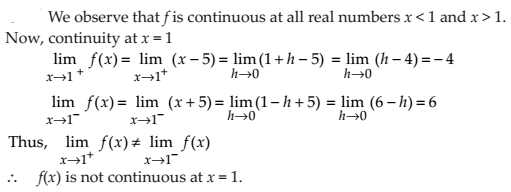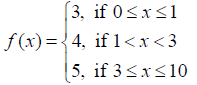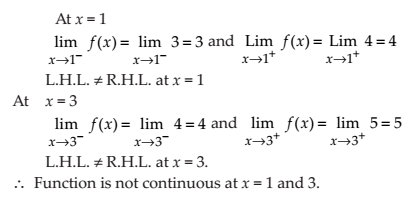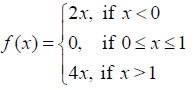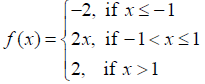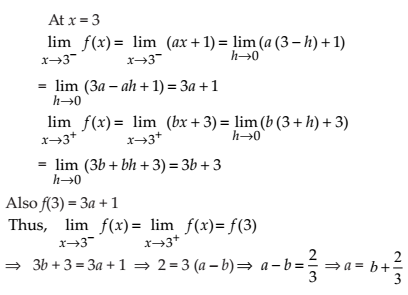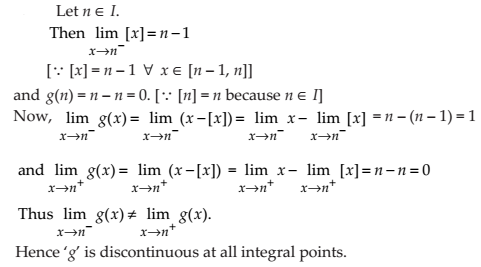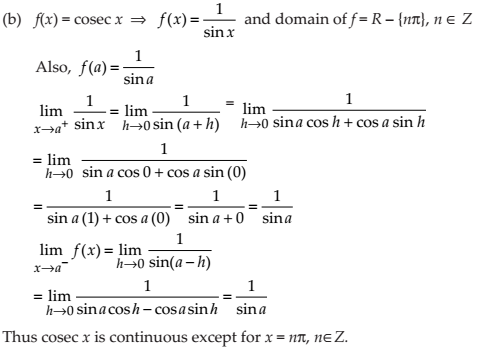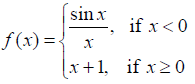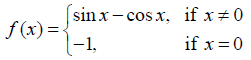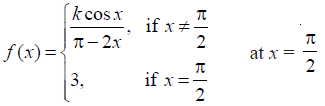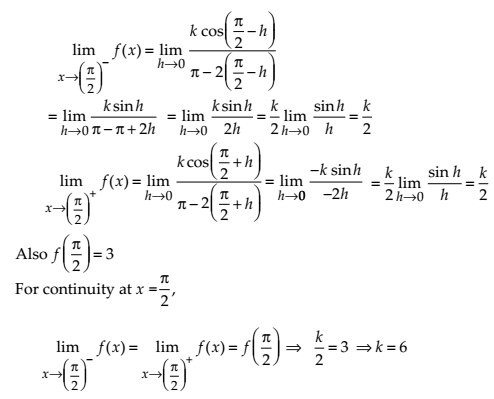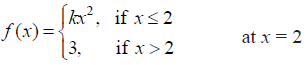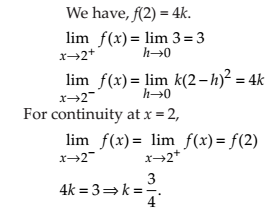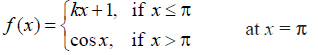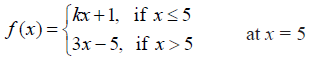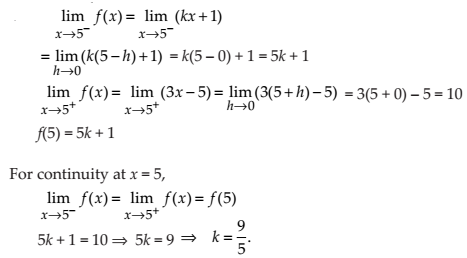NCERT Solutions for Class 12 Maths Continuity and Differentiability
Hi Students, Welcome to Amans Maths Blogs (AMB). In this post, you will get the NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1. This NCERT Solutions can be downloaded in PDF file. The downloading link is given at last.
CBSE Class 12th is an important school class in your life as you take some serious decision about your career. And out of all subjects, Maths is an important and core subjects. So CBSE NCERT Solutions for Class 12th Maths is major role in your exam preparation as it has detailed chapter wise solutions for all exercise.
NCERT Solutions for Class 12 Maths are not only the solutions of Maths exercise but it builds your foundation of other important subjects. Getting knowledge of depth concept of CBSE Class 12th Maths like Algebra, Calculus, Trigonometry, Coordinate Geometry help you to understand the concept of Physics and Physical Chemistry.
As we know that all the schools affiliated from CBSE follow the NCERT books for all subjects. You can check the CBSE NCERT Syllabus. Thus, NCERT Solutions helps the students to solve the exercise questions as given in NCERT Books.
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 1.
Prove that the function f (x) = 5x – 3 is continuous at x = 0, at x = – 3 and at x = 5.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 2.
Examine the continuity of the function f (x) = 2x2 – 1 at x = 3.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 3.
Examine the following functions for continuity.
(a) f (x) = x – 5
NCERT Solutions:
(b) f (x) = 1 / (x – 5)
NCERT Solutions:
(c) f (x) = (x2 – 25) / (x + 5)
NCERT Solutions:
(d) f (x) = | x – 5 |
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 4.
Prove that the function f (x) = xn is continuous at x = n, where n is a positive integer.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 5.
Is the function f defined by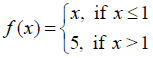 
continuous at x = 0? At x = 1? At x = 2?
NCERT Solutions:
Find all points of discontinuity of f, where f is defined by
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 6.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 7.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 8.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 9.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 10.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 11.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 12.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 13.
Is the function defined by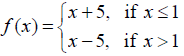 
a continuous function?
NCERT Solutions:
Discuss the continuity of the function f, where f is defined by
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 14.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 15.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 16.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 17.
Find the relationship between a and b so that the function f defined by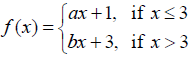 
is continuous at x = 3.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 18.
For what value of λ is the function defined by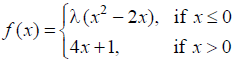 
continuous at x = 0? What about continuity at x = 1?
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 19.
Show that the function defined by g (x) = x – [x] is discontinuous at all integral points. Here [x] denotes the greatest integer less than or equal to x.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 20.
Is the function defined by f (x) = x2 – sin x + 5 continuous at x = π?
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 21.
Discuss the continuity of the following functions:
(a) f (x) = sin x + cos x
NCERT Solutions:
(b) f (x) = sin x – cos x
NCERT Solutions:
(c) f (x) = sin x . cos x
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 22.
Discuss the continuity of the cosine, cosecant, secant and cotangent functions.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 23.
Find all points of discontinuity of f, where 
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 24.
Determine if f defined by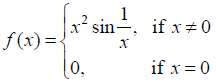 
is a continuous function?
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 25.
Examine the continuity of f, where f is defined by
NCERT Solutions:
Find the values of k so that the function f is continuous at the indicated point in Exercises 26 to 29.
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 26.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 27.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 28.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 29.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 30.
Find the values of a and b such that the function defined by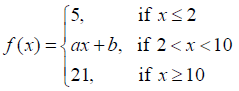 
is a continuous function.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 31.
Show that the function defined by f (x) = cos (x2) is a continuous function.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 32.
Show that the function defined by f (x) = | cos x | is a continuous function.
NCERT Solutions:
We know that cosine function is every where continuous and also modulus function is continuous. Thus, |cos x| is continuous everywhere.
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 33.
Examine that sin | x | is a continuous function
NCERT Solutions:
Let f(x) = |x| and g(x) = sin x. Then, (gof)(x) = g[f(x)] = g(|x|) = sin|x|. Now, f and g are being continuous, it follows that their composite (gof) is also continuous functions.
NCERT Solutions for Class 12 Maths Continuity and Differentiability Exercise 5.1: Ques No 34.
Find all the points of discontinuity of f defined by f (x) = | x | – | x + 1 |.
NCERT Solutions:
