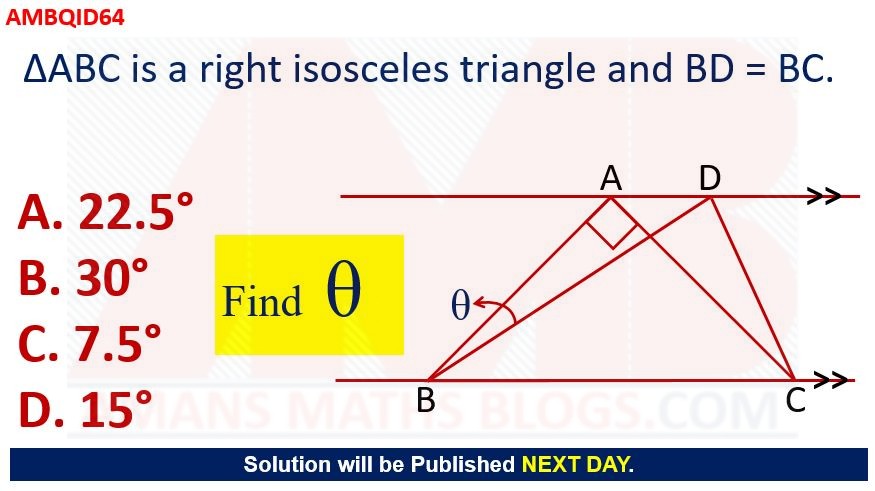
AMBQID 64:

In the given figure, the triangle ABC is a right isosceles triangle and BD = BC. Find the value of θ.

Options:

A. 22.5 Degree

A. 30 Degree

A. 7.5 Degree

D. 15 Degree

Solution:

To solve the above question, we need to use the following math concepts.

Concept 1: The perpendicular distance between the parallel lines is same at any points

Concept 2: In a right triangle, the Pythagoras theorem is used. It the square of the hypotenuse is the sum of the squares of the perpendicular and the square of the base. 

Concept 3: In a right isosceles triangle, the two perpendicular lines are equal and each acute angle is 45 degree.

Concept 4: In an isosceles triangle, the perpendicular drawn from the vertex to opposite side bisects the side.

Concept 5: In trigonometry, sin(Angle) = Perpendicular / Hypotenuse.

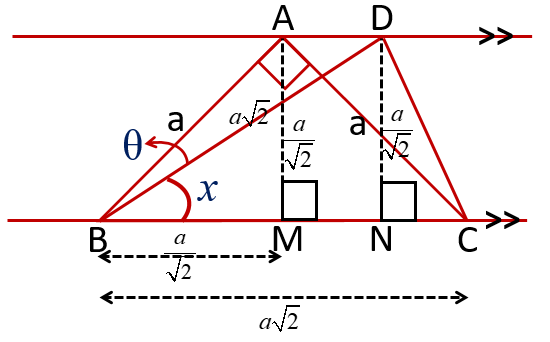
Let the sides of right isosceles triangle AB = AC = a. Then, BC =  by using Concept 2.

Since AB = AC = a, then angle ABC = 45 degree using concept 3.

Given that BD = BC. Thus BD = .

Now, in isosceles triangle ABC, drawn a perpendicular AM from the vertex A to the opposite side BC. Thus, BM = MC = BC/2 by using concept 4. Hence, BM = .

In right triangle ABM, AM =  using concept 2.

Since the lines AD and MN are parallel, then AM = DN by using concept 1. Thus, DN = . Now, let angle DBN = x.

Using concept 5, we get sin x = DN / BD = 1/2. Thus, x = 30 degree.

Therefore, θ = 45 degree – 30 degree = 15 degree. The correct option is D 15 degree.

 

Some Important Questions

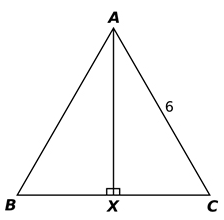
The figure below is an equilateral triangle with sides of length 6. What is the area of the triangle?  

Since the triangle is an equilateral triangle, its angles are 60°.

Therefore, the vertical line AX bisects the angle BAC, so it splits it into two congruent angles of 30° each.

So, the two smaller triangles are 30-60-90 triangles. Thus, the ratio of the lengths of the sides is 1: :2.

The area of a triangle is given by the formula , where b is the length of the base and h is the height. In the figure, the base is 3 + 3 = 6 and the height is 3.

Substitute these values into the formula and calculate the area as A = (1/2) x 6 x 3 = 9

Which of the following could be the side lengths of a right triangle?

Options:

A. 4, 5, and 6

A. 4, 9, and 10

A. 5, 10, and 15

D. 5, 12, and 13

If a triangle is a right triangle, then the lengths of its sides satisfy the Pythagorean Theorem,

In a right triangle, the Pythagoras theorem is used. It the square of the hypotenuse is the sum of the squares of the perpendicular and the square of the base. a² + b² = c² .

To determine which choice is correct, test each set of values by substituting them into the Pythagorean Theorem. Start with the first set of numbers: 3, 13, and 14. 

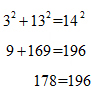
Since the result is not a true equality, the first set of values does not represent the side lengths of a right triangle. Test the other four choices. The only values that satisfy the Pythagorean Theorem are 5, 12, and 13

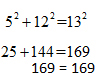
The circumference of a circle is 30. What is its area?

Options:

A. 225

B. 900

C. 400

D. 3000

The circumference of a circle is given by the formula C = 2, where r is the radius of the circle.

Substitute the given circumference into this formula and solve for r.
30 = 2
r = 15

Therefore, the radius of the circle is 15.

Thus, the area of a circle is given by the formula A= ².  Substitute the length of the radius into this formula and calculate the area.
A =(15)² = 225

 

amans maths blogs