Top 120 Geometry Concept Tips and Tricks For Competitive Exams JSTSE NTSE NSEJS SSC
In this post, you will get Top 120 Geometry Concept Tips and Tricks that will help you to solve geometrical problems of competitive exams like SSC CGL CHSL, CAT, IBPS Bank, NTSE, NSEJS and JSTSE etc.
ANGLES
In this section, you will learn Geometry Concept Tips and Tricks of Angles Related Problems.
Geometry Concept: 1 ANGLE
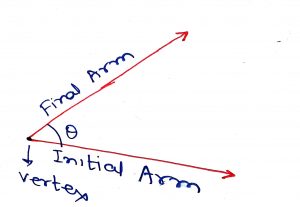
An ANGLE is the amount of rotation from initial arm to final arm which share a common endpoint. The arms are known as the sides of the angle and the common point is known is the vertex of the angle.
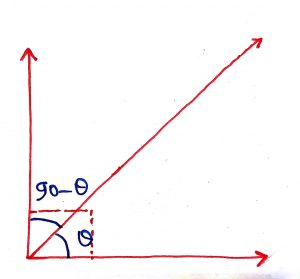
Geometry Concept: 2 COMPLEMENTARY ANGLES
If the sum of any two angles is equal to 90 degree or one right angle, then both the angles are known as COMPLEMENTARY ANGLES to each other. If the two complementary angles are adjacent angles then their non-common arms are either sides of common side and they form a right angle.
Geometry Concept: 3 SUPPLEMENTARY ANGLES
If the sum of any two angles is equal to 180 degree or two right angle, then both the angles are known as SUPPLEMENTARY ANGLES to each other. If the two supplementary angles are adjacent, then their non-common sides form a straight line. Such angles are also known as Linear Pair of Angles.
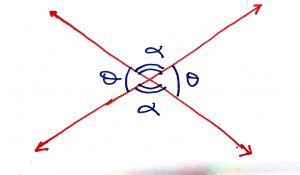
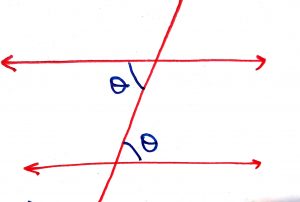
Geometry Concept: 4 VERTICALLY OPPOSITE ANGLES.
A pair of angles opposite to each other formed by two intersecting straight lines that form an X-like shape are called VERTICALLY OPPOSITE ANGLES. They are always equal.
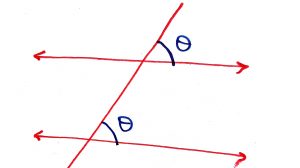
Geometry Concept: 5 CORRESPONDING ANGLES POSTULATE
If two parallel lines are intersected by a transvarsal line, then their corresponding angles are equal. This is a CORRESPONDING ANGLES POSTULATE.
Geometry Concept: 6 ALTERNATE INTERIOR ANGLE THEOREM
If two parallel lines are intersected by a transversal, then their alternate angles are equal. This is known as ALTERNATE INTERIOR ANGLE THEOREM.
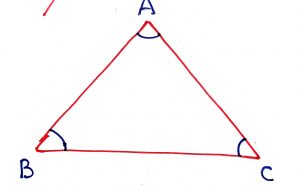
Geometry Concept: 7 ANGLES SUM PROPERTY OF TRIANGLE
The sum of all interior angles in a triangle is 180 degree. The sum of all exterior angles of the triangle is 360 degree. This is known as ANGLES SUM PROPERTY OF TRIANGLE.
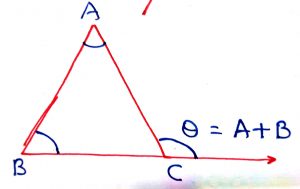
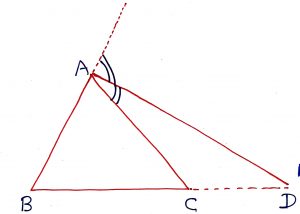
Geometry Concept : 8 EXTERIOR ANGLES PROPERTY OF TRIANGLE
The exterior angle of a triangle is the sum of two opposite interior angles. This is known as EXTERIOR ANGLES PROPERTY OF TRIANGLE.
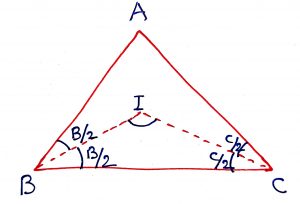
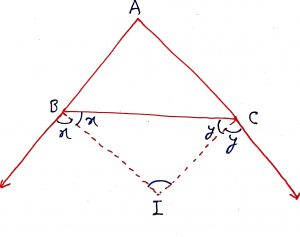
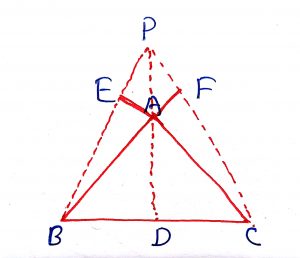
Geometry Concept : 9 BISECTOR OF INTERIOR ANGLES
If the bisectors of angles ABC and ACB of a triangle ABC meet at a point I, then angle BIC =
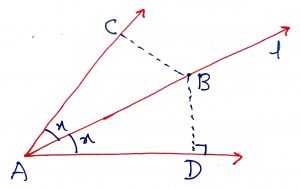
Geometry Concept : 10 BISECTOR OF EXTERIOR ANGLES
The sides AB and AC of a triangle ABC are produced to P and Q respectively. If the bisectors of angle PBC and QCB intersects at I then BIC = .
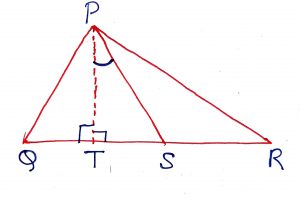
Geometry Concept : 11 FIND ANGLE
In a triangle PQR, if PS is the bisector of angle QPR (where angle Q > angle R) and PT QR, then angle TPS =
. If the angle Q < angle R, then TPS =
.
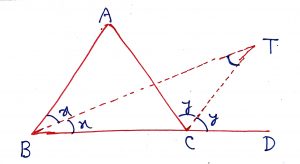
Geometry Concept : 12 FIND ANGLE
The angles between internal bisector of one base angle and the external bisector of the other base angle of a triangle is equal to one half of the vertical angle. Thus, we have angle BTC = .
Geometry Concept : 13 FIND ANGLE
In n-point star sum of all the angles at its vertices is . Thus, in a five-point star, we have the sum of all angles A + B + C+ D+ E =
.
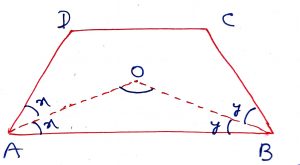
Geometry Concept: 14 FIND ANGLE
In a quadrilateral ABCD, if AO and BO are the bisectors of angles A and B respectively, then
angle AOB = .
Geometry Concept: 15 SUM OF ALL ANGLES IN POLYGON
In any n sides convex polygon, the sum of all angles is and the sum of all exterior angles (taken in one direction, either clockwise of counter clock wise) in any convex polygon is
.
Geometry Concept: 16 IMPORTANT RESULT
Two internal angle bisector of any two angles of a triangle cannot be perpendicular.
Geometry Concept: 17 IMPORTANT RESULT
A convex polygon cannot have more than three acute internal angles.
CONGRUENT TRIANGLES
In this section, you will learn Geometry Concept Tips and Tricks of Congruent Triangles Related Problems.
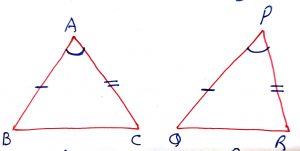
Geometry Concept: 18 Side-Angle-SIde (SAS) CONGRUENCE
Two angles are congruent, if two sides and the included angle of first triangle are equal to the corresponding sides and the included angle of the other triangle. In the figure below, AB = PQ angle A = angle P and AC = PR. Thus,
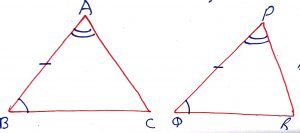
Geometry Concept: 19 Angle-Side-Angle (ASA) CONGRUENCE
Two angles are congruent, if two angles and the included sides of first triangle are equal to the corresponding angles and the included side of the other triangle. In the figure, AB = PQ angle A = angle P and angle B = angle Q. Thus,
Geometry Concept: 20 Angle-Angle-Side (AAS) CONGRUENCE
Two angles are congruent, if two angles and any non-included sides of first triangle are equal to the corresponding angles and the side of the other triangle. This is same as ASA Congruency.
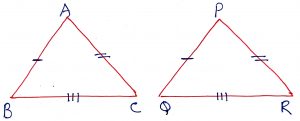
Geometry Concept: 21 Side-Side-Side (SSS) CONGRUENCE
Two angles are congruent, if the three sides of first triangle are equal to the corresponding three sides of the other triangle. In the figure, AB = PQ, AC = PR and BC = QR. Thus,
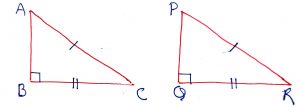
Geometry Concept: 22 Right Angle-Hypotenuse-Side (RHS) CONGRUENCE
Two angles are congruent, if the hypotenuse and one side of the first triangle are respectively equal to the hypotenuse and one side of the other triangle. In the figure, angle B = angle Q = 90 degree, AC = PR and BC = QR. Thus,
ISOSCELES TRIANGLE
In this section, you will learn Geometry Concept Tips and Tricks of Isosceles Triangles Related Problems.
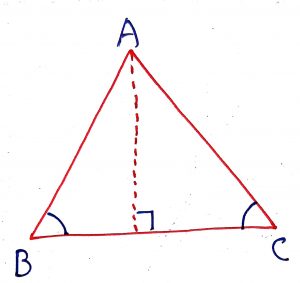
Geometry Concept: 23 PROPERTY
Angles opposite to two equal sides of a triangle are equal. It means the base angles are equal.
Geometry Concept: 24 PROPERTY
The altitude drawn from one vertex of a triangle bisects the opposite side. It means the altitude and the median from the same vertex are same.
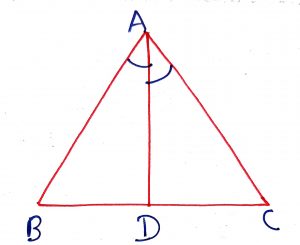
Geometry Concept: 25 PROPERTY
The bisector of the vertical angle bisects the base of the isosceles triangle.
Geometry Concept: 26 PROPERTY
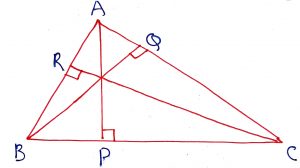
Line l is the bisector of angle A and b is any point on l. BP and BQ are perpendiculars from B to the sides of the angle A. Then BP = BQ or B is outdistance from the sides of the angle A. That means, each point on the angle bisector is equidistant from the sides of the angle.
TRIANGLE INEQUALITIES
In this section, you will learn Geometry Concept Tips and Tricks of Triangle Inequalities Related Problems.
Geometry Concept: 27 PROPERTY
If the two sides of a triangle are unequal, the longer sides has the greater angles opposite to it.
Geometry Concept: 28 PROPERTY
In a triangle, the greater angle has the longer side opposite to it.
Geometry Concept: 29 PROPERTY
The sum of any two sides of a triangle is greater than the third side.
Geometry Concept: 30 PROPERTY
The difference of any two sides of triangle is less than the third side.
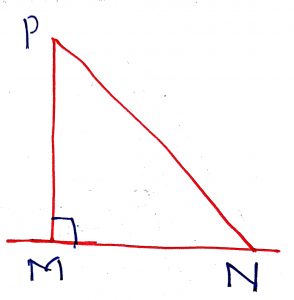
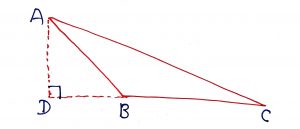
Geometry Concept: 31 PROPERTY
Of all the line segments that can be drawn to a given line, from a point not laying on it the perpendicular line segment is the shortest. In the figure, PM < PN
Geometry Concept: 32 PROPERTY
The sum of the three altitudes of a triangle is less than the sum of the three sides of the triangle. In the figure, AP + BQ + CR < AB + BC + CA
Geometry Concept: 33 IMPORTANT RESULT
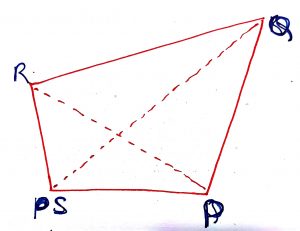
In a quadrilateral PQRS, PQ is the longest side and RS is shortest side. Then, and
.
Geometry Concept: 34 IMPORTANT RESULT
In a quadrilateral PQRS, diagonals PR and QS intersect at O. Then
(i) PQ + QR + RS + SP > PR + QS
(ii)PQ + QR + RS + SP < 2(PR + QS).
Geometry Concept: 35 IMPORTANT RESULT
O is any point in the interior of triangle ABC, then
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + OB + OC
(iii) OA + OB + OC > (AB + BC + CA)
Geometry Concept: 36 IMPORTANT RESULT
In any triangle, the sum of any two sides is greater than the twice median drawn to the third side.
Geometry Concept: 37 IMPORTANT RESULT
In a triangle with the sides length a, b, and c and the medians length ma, mb and mc,
AREA RELATED Geometry ConceptS
In this section, you will learn Geometry Concept Tips and Tricks of Area of Triangles Related Problems.
Geometry Concept: 38 IMPORTANT RESULT
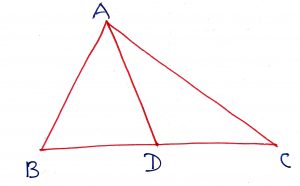
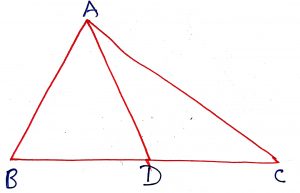
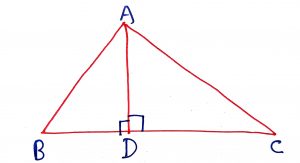
If D is any point the side BC of a triangle ABC, then
Geometry Concept: 39 IMPORTANT RESULT
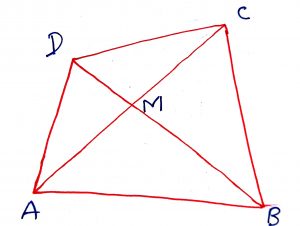
In ABCD is any quadrilateral, the diagonals AC and BD intersects at M. Then, .
Geometry Concept: 40 IMPORTANT RESULT
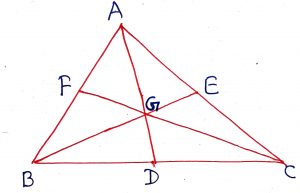
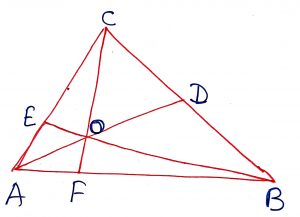
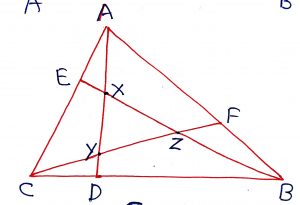
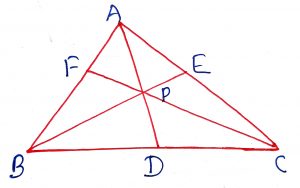
D, E and F are the points on the sides BC, CA, AB respectively of triangle ABC, such that AD, BE and CF are concurrent at P, then
(i) (ii)
(iii)
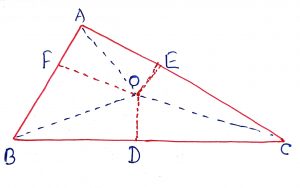
Geometry Concept: 41 IMPORTANT RESULT
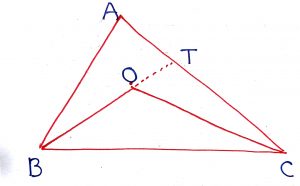
A triangle ABC is divided into six smaller triangles by lines drawn from the vertices through a common interior point as shown in the figure. Then, use the following relation to find the unknown area of the smaller triangle.
(i) (ii)
(iii)
MID POINTS OF SIDES
In this section, you will learn Geometry Concept Tips and Tricks of Mid Point of Sides of Triangles Related Problems.
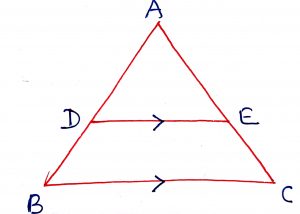
Geometry Concept: 42 MID POINT THEOREM
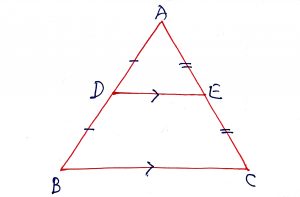
The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and half of it. In a triangle ABC, D and E are the mid points of AB and AC, then DE || BC and
DE = BC.
Geometry Concept: 43 IMPORTANT RESULT
The line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Geometry Concept: 44 MEDIANS
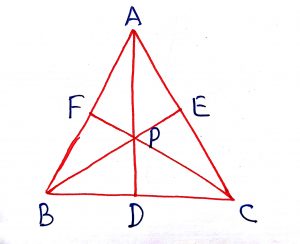
In a triangle ABC, the mid-points of the sides BC CA and AB are D E and F respectively. The lines AD BE and CF are called medians of the triangle ABC, the point of concurrency of the three medians is called centroid. The centroid divides the medians in the ratio of 2:1 from the vertex to the side. The centroid is denoted by G. Then,
(i) (ii)
,
,
(iii)
Geometry Concept: 45 IMPORTANT RESULT
The mid point of the hypotenuse of a right angle triangle is equidistant from all its vertices. In a triangle ABC with angle B = 90 degree and D is the mid point of its hypotenuse, then BD = AC.
Geometry Concept: 46 IMPORTANT RESULT
The line segment joining the mid points of the diagonals of a trapezium is parallel to each of the parallel sides and is equal to the half of the difference of these sides. In the figure, ABCD is a trapezium and P and Q are the mid-points of the diagonals AC and BD, then for AB > CD and
for AB<CD.
Geometry Concept: 47 IMPORTANT RESULT
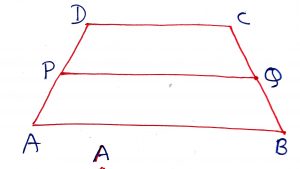
The line segment joining the mid points of the non-parallel sides of a trapezium is parallel to each of the parallel sides and is equal to the half of the sum of the parallel sides of the trapezium. In the figure, ABCD is a trapezium and P and Q are the mid-points of the non-parallel sides AD and BC, then
BASIC PROPORTIONALITY THEOREM
In this section, you will learn Geometry Concept Tips and Tricks of Basic Proportionality Theorem of Thele’s Theorem Related Problems.
Geometry Concept: 48 BASIC PROPORTIONALITY THEOREM or THALES THEOREM
If a line is drawn parallel to one side of a triangle intersecting the other two sides, at distinct points, then it divides the other two sides in the same ratio. In the figure, ABC is a triangle with DE || BC. Then,we have the following result (i) (ii)
(iii)
(iv)
(v)
(vi)
.
Geometry Concept: 49 Converse of BASIC PROPORTIONALITY THEOREM or THALES THEOREM
If a line divides any two sides of a triangle in the same ratio then the line must be parallel to the third side. In the figure, ABC is a triangle. If , then DE || BC.
Geometry Concept: 50 IMPORTANT RESULT
On the sides BC, CA, AB of a triangle ABC, points D, E F are taken in such a way that . Then the area of the triangle XYZ determined by the lines AD, BE and CF is
the of the area of the triangle ABC. It means
.
ANGLES BISECTOR THEOREM
In this section, you will learn Geometry Concept Tips and Tricks of Angles Bisector Theorem Related Problems.
Geometry Concept: 51 INTERNAL ANGLES BISECTOR THEOREM
The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle. In the figure, ABC is a triangle. If AD bisects the angle A, then (i) (ii)
Geometry Concept: 52 EXTERNAL ANGLES BISECTOR THEOREM
The external bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle. In the figure, ABC is a triangle. If AD bisects the exterior angle A and intersects BC produced in D, then .
Geometry Concept: 53 LENGTH OF ANGLE BISECTOR
(i) If the internal angle bisector of angle A meets the opposite side BC at D, then
(ii) If the internal angle bisector of angle B meets the opposite side AC at E, then
(iii) If the internal angle bisector of angle C meets the opposite side AB at F, then
SIMILAR TRIANGLE
In this section, you will learn Geometry Concept Tips and Tricks of Similar Triangles Related Problems.
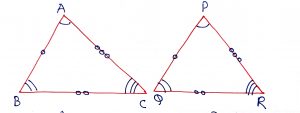
Geometry Concept: 54 Side-Side-Side (SSS) SIMILARITY
If in two triangles the sides of one triangle are proportional to those of the other, then the triangles are similar and hence the corresponding angles of the two triangles are equal. In the figure, ABC and PQR are two triangles such that , then
and hence the angles
.
Geometry Concept: 55 Angle-Angle-Angle (AAA or AA) SIMILARITY
If in two triangles the angles of one triangle are proportional to those of the other, then the triangles are similar and hence the sides opposite to those angles are proportional. In the figure, ABC and PQR are two triangles such that , then
and hence
Geometry Concept: 56 Side-Angle-Side (SAS) SIMILARITY
If in two triangles, one angle of one triangle is equal to one angle of the other triangle and sides containing these angles are proportional, then two triangles are similar and hence remaining corresponding angles are equal and the sides opposite to those angles are in the same proportional. In the figure, ABC and PQR are two triangles such that angle A = angle P and , then
and hence the angles
and
.
Geometry Concept: 57 AREA RATIO THEOREM FOR SIMILAR TRIANGLES
The ratio of the areas of two similar triangles are equal to the ratio of the squares of any two corresponding sides. In the figure, ABC and PQR are two triangles such that , it means angles
and
, then
.
Geometry Concept: 58 IMPORTANT RESULT
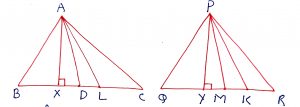
In the triangles ABC and PQR, if AD and PM are the medians, AX and PY are the altitudes AL and PK are the angle bisectors and S1 and S2 be their semi-perimeters respectively, then .
Geometry Concept: 59 IMPORTANT RESULT
There is a unique triangle with sides length as 4, 5 and 6 units whose sides lengths are consecutive integers and one of whose angles is twice the other.
RIGHT ANGLE RELATED THEOREM
In this section, you will learn Geometry Concept Tips and Tricks of Right Angled Triangle Related Problems.
Geometry Concept: 60 IMPORTANT RESULT
If a perpendicular AD is drawn from the right angled vertex A of a right angled triangle ABC to the hypotenuse BC then the triangles on both sides of the perpendicular are similar to the whole triangles and to each other and hence ,
, and
.
Geometry Concept: 61 PYTHAGORAS THEOREM
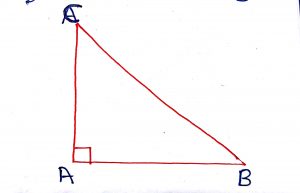
In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. In the figure, ABC is a right angled triangle with angle A = 90 degree, then .
Geometry Concept: 62 ACUTE ANGLED TRIANGLE THEOREM
In a triangle ABC, if angle B < 90 degree and AD BC, then
Geometry Concept: 63 OBTUSE ANGLED TRIANGLE THEOREM
In a triangle ABC, if angle B > 90 degree and AD BC, then
.
Geometry Concept: 64 IMPORTANT RESULT
In a triangle ABC, if , then the triangle ABC is an acute angled triangle with B is acute angle. If
, then the triangle ABC is an obtuse angled triangle with B is obtuse angle.
APOLLONIUS THEOREM
In this section, you will learn Geometry Concept Tips and Tricks of Apollonius Theorem Related Problems.
Geometry Concept: 65 APOLLONIUS THEOREM
In any triangle, the sum of the squares of any two sides is equal to twice the square of half of the third side together with twice the square of the median which bisects the third side. This theorem is used to find the length of the median of any triangle. In the figure, ABC is a triangle, in which AD, BE and CF are the medians which bisects the sides BC, AC and AB respectively. Thus, according to this theorem,
(i)
(ii)
(iii)
Geometry Concept: 66 IMPORTANT RESULT
In any triangle, the three times the sum of the squares of three sides of a triangle is equal to four times the sum of the squares of its medians. In the figure, ABC is a triangle, in which AD, BE and CF are the medians which bisects the sides BC, AC and AB respectively. Then, .
STEWART THEOREM
In this section, you will learn Geometry Concept Tips and Tricks of Stewart Theorem.
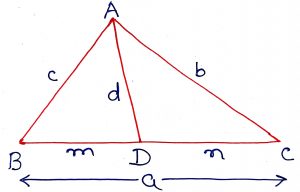
Geometry Concept: 67 STEWART THEOREM
In a triangle ABC, if D is a point on side BC such that BD = m and DC = n and AD = d, then . To remember this theorem, use the trick
or A man (product of m, a and n) and his dad (product of d, a and d) put a bomb (product of b, m and b)in the sink (product of c, n and c).
Geometry Concept: 68 STEWART THEOREM FOR MEDIAN
In the STEWART THEOREM, if AD is the median then and the median AD = ma. Thus, by the STEWART THEOREM, we get
. This is the APOLLONIUS THEOREM and the median lengths are
(i)
(ii)
(iii)
Geometry Concept: 69 STEWART THEOREM FOR ANGLE BISECTOR
In the STEWART THEOREM, if AD is the angle bisector then and
, AD = ta. Thus, by the STEWART THEOREM, we get
.
Thus, the length of the angle bisectors are
(i)
(ii)
(iii)
QUADRILATERAL
In this section, you will learn Geometry Concept Tips and Tricks of Quadrilaterals.
Geometry Concept: 70 PRALLELOGRAM
A quadrilateral whose both pair of opposite sides are parallel known as parallelogram. Some of the properties of a parallelogram are below.
1 A diagonal of a parallelogram divides it into two congruent triangles.
2.In a parallelogram, the opposite sides are equal.
3.Two opposite angles are equal.
4. The diagonals of a parallelogram bisects each other.
5. In a parallelogram, the bisectors of any two consecutive angles intersects at right angle.
6. The angle bisector of a parallelogram form a rectangle.
7. In a parallelogram, the sum of any two consecutive angles is 180 degree.
8. In a quadrilateral, if both opposite sides are equal then, it is a parallelogram.
9. In a quadrilateral, if both opposite angles are equal then it is a parallelogram.
10. If the diagonals of quadrilateral bisects each other then it is a parallelogram.
11. If one pair of opposite sides equal and parallel then it is a parallelogram.
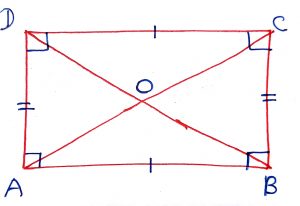
Geometry Concept: 71 RECTANGLE
A parallelogram in which anyone angle is right angle is called as rectangle. Some of the properties of a rectangle are below.
1. opposite sides are parallel and equal.
2. Opposite angles are equal and each of 90 degree.
3. Diagonals are equal and bisects each other.
4. When a rectangle is inscribed in a circle the diameter of the circle is equal to the diagonal of the rectangle.
5.For a given parameter of rectangle, a square has the maximum area.
6. The quadrilateral formed by joining the intersection of the angle bisector of a parallelogram is a rectangle.
7. If P is any point in the plane of the rectangle ABCD, then PA2 + PC2 = PB2 + PD2.
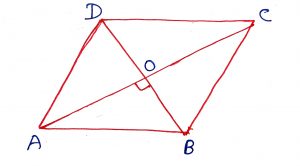
Geometry Concept: 72 RHOMBUS
A parallelogram in which any two adjacent sides are equal or all sides are equal, then it is called rhombus. Some of the properties of a rhombus are below.
1. Opposite sides are parallel.
2. All sides are equal.
3. Diagonals are perpendicular bisects the opposite pair of angles.
4. Diagonals bisects the opposite pair of angles.
5. A parallelogram is rhombus if its diagonals are perpendicular to each other.
6. Any parallelogram circumscribing a circle is a rhombus.
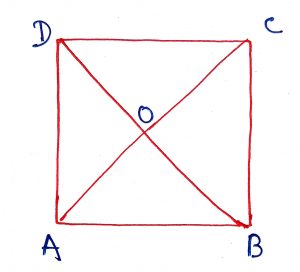
Geometry Concept: 73 SQUARE
A square is a rectangle whose all sides are equal or a rhombus whose all angles equal. Thus each square is a parallelogram, a rectangle and a rhombus. Some of the properties of a square are below.
1. All sides are equal.
2. Opposite pair of sides are equal.
3. Diagonals are equal and are perpendicular bisector to each other.
4. Diagonal of an inscribed square is equal to the diameter of the circumscribing circle.
5. Sides of a circumscribing square is equal to the diameter of the inscribed circle.
6. Angles formed by the diagonals and a side of the square is each equal to 45 degree.
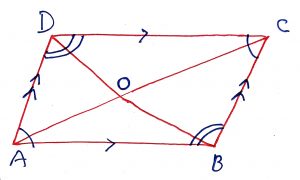
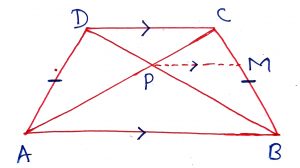
Geometry Concept: 74 TRAPEZIUM
A quadrilateral whose one pair of sides is parallel known as trapezium. Some of the properties of a square are below.
1. The line joining the mid points of the non-parallel sides is half the sum of the parallel sides.
2. If the non-parallel sides are equal then the diagonals will also be equal to each to other and converse is also true. The corresponding trapezium is called ISOSCELES TRAPEZIUM.
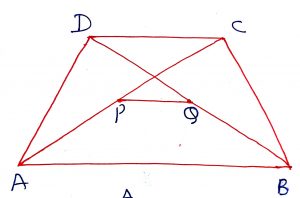
3. Diagonals intersects each other proportionally in the ratio of the lengths of the parallel sides. In the figure, ABCD is a trapezium in which AC and BD intersects each other at P, then .
4. By joining the midpoints of the adjacent sides of the trapezium four similar triangles are obtained.
5. If a trapezium is inscribed in a circle then it is an isosceles trapezium with non-parallel sides.
6. In an isosceles trapezium base angles are equal and other two angles are also equal.
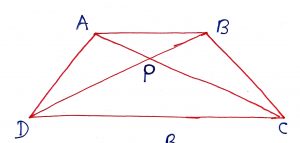
Geometry Concept: 75 ISOSCELES TRAPEZIUM
If ABCD is an isosceles trapezium and the diagonals intersects at P then the following results are true.
(i) Non-parallel sides are equal, AD = BC
(ii) AC = BD
(iii) AP = PB and PD = PC
(iv) PA PC = PB
PD
(v)
(vi) Angle PAB = Angle PBA = Angle PDC = Angle PCD
(vii) Angle DAB = Angle CBA and Angle ADC = Angle BCD
(viii) Angle PAD = Angle PBC and Angle ADB = Angle ACB
(ix)
(x) If PM || AB || CD then
(xi) ABCD is a cyclic quadrilateral and then all the properties of the cyclic quadrilateral also applicable.
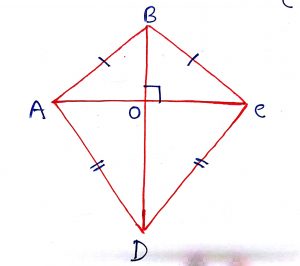
Geometry Concept: 76 KITE
In a kite two pair of adjacent sides equal. Some of the properties of the kites are given below.
(i) AB = BC and AD = CD
(ii) Diagonals intersects at right angle.
(iii) Longer diagonal is the perpendicular bisector of the shorter diagonal.
(iv) The quadrilateral formed by the mid-points of the adjacent the sides of the kite is rectangle.
(v) Area of the Kite = (Product of the diagonals).
CONCURRENCY AND COLLINEARITY
In this section, you will learn Geometry Concept Tips and Tricks of Concurrency & Col-linearity.
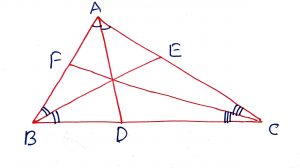
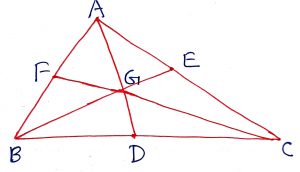
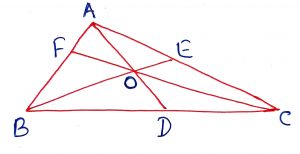
Geometry Concept: 77 CEVIAN
A line segment joining a vertex of a triangle to any point on the opposite side or the point may be the extension of the opposite side also is called a Cevian. In the figure, AD, BE and CF are the cevians of the triangle ABC.
Geometry Concept: 78 CONCURRENT LINES
Three straight lines are said to be concurrent if all the three lines passes through a common point.
Geometry Concept: 79 Three points are said to be collinear, if they lie on a straight line. If A, B and C are the three points on a straight line in order, then AB, BC and AC are taken to be positive and BA, CB and CA are taken to be negative. Thus, AB + BC = AC and AB + BC + CA = 0.
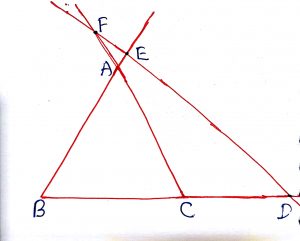
Geometry Concept: 80 CARNOT’S THEOREM
Let D, E and F be points on sides BC, AC and AB respectively of triangle ABC. Then, the perpendiculars to the sides of the triangle at points D, E and F are concurrent if and only if
Geometry Concept: 81 CEVA’S THEOREM
If points D, E and F are taken on the sides BC, CA and AB of the triangle ABC so that the lines AD, BE and CF are concurrent at a point P (Inside or outside), then or
.
Geometry Concept: 82 VAN AUBEL THEOREM
If points D, E and F are taken on the sides BC, CA and AB of the triangle ABC so that the lines AD, BE and CF are concurrent at a point P, then
(i)
(ii)
(iii)
Geometry Concept: 83 CONVERSE OF CEVA’S THEOREM
If three cevians AD, BE and CF satisfy , then the three cevians are concurrent.
Thus, the following results are true.
(i) The medians of a triangle are concurrent.
(ii) The altitudes of a triangle are concurrent.
(iii) The internal bisectors of the angles of a triangle are concurrent.
(iv) The internal angle bisector of an angle of a triangle and the other two external bisectors are concurrent.
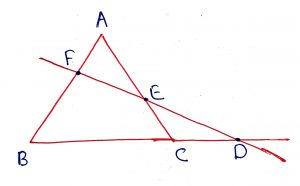
Geometry Concept: 84 MENELAUS THEOREM
If a transversal cuts (Internally or externally) the sides BC, CA and AB of a triangle at D, E and F respectively then
Geometry Concept: 85 IMPORTANT RESULT
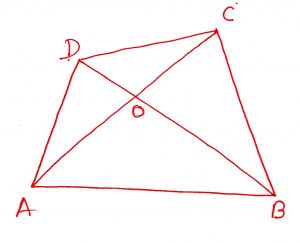
A transversal cuts the sides AB, BC, CD, DA of quadrilateral at P, Q, R and S respectively, then
Geometry Concept: 86 IMPORTANT RESULT
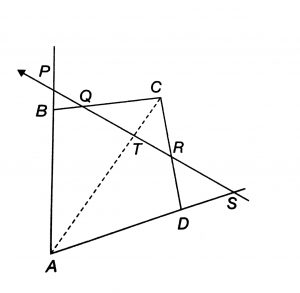
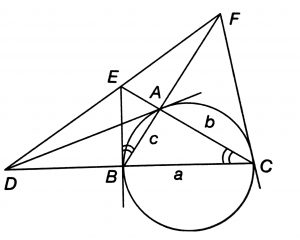
The tangents at the vertices of a triangle to its circumcircle meets the opposite sides in three collinear points. In the figure, ABC is a triangle. The tangent to its circumcircle at A meets opposite side produce BC at D. The tangent to its circumcircle at B meets opposite side produce CA at E. The tangent to its circumcircle at C meets opposite side produce BA at F. Then, the points D, E and F are collinear.
CIRCLE
In this section, you will learn Geometry Concept Tips and Tricks of Circles.
Geometry Concept: 87 PROPERTY
One and only one circle can be drawn so as to pass three non-collinear points.
Geometry Concept: 88 PROPERTY
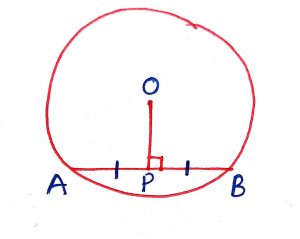
The perpendicular drawn from the center of a circle to a chord of the circle bisects the chord. Conversely, the straight line joining the mid-points of chord of circle to the center is perpendicular to the chord.
Geometry Concept: 89 PROPERTY
Equal chords of a circle are equidistant from the center. Conversely, if two chords are equidistant from the center then they are equal.
Geometry Concept: 89 PROPERTY
In the same circle or in equal circles, equal chords cut off equal arcs and conversely.
Geometry Concept: 91 PROPERTY
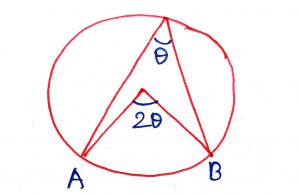
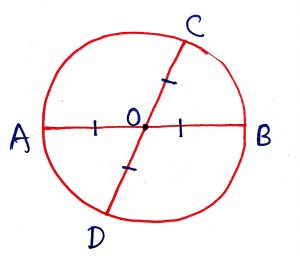
Angle subtended by an arc of a circle at the center of the circle is twice the angle subtended by the same arc at any point on the remaining part of the circle.
Geometry Concept: 92 PROPERTY
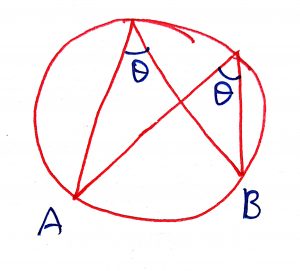
Angles in the same segment of a circle are equal and conversely.
Geometry Concept: 93 PROPERTY
Angle in a semi-circle is right angle. Angle in a segment smaller than a semi-circle is an obtuse angle and angle in a segment bigger than a semi-circle is an acute angle.
Geometry Concept: 94 PROPERTY
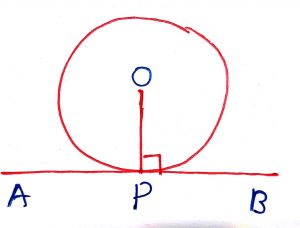
Radius drawn at point of contact of a tangent to the circle is perpendicular to the tangent.
Geometry Concept: 95 PROPERTY
From an external point we can draw two tangents to the circle. Both the tangents are equal in length.
Geometry Concept: 96 PROPERTY
If two chords of a circle bisects each other, they are diameters.
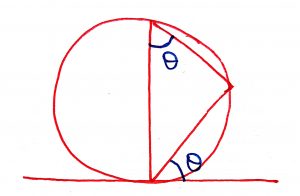
Geometry Concept: 97 ALTERNATE SEGMENT THEOREM
If through a point on a circle, a tangent and a chord be drawn the angle which the tangent makes with the chord is equal to the angle in the alternate segment.
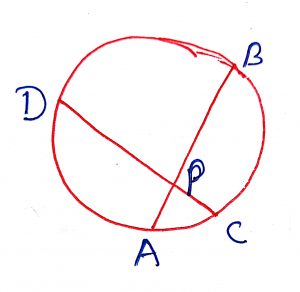
Geometry Concept: 98 INTERSECTING CHORDS THEOREM
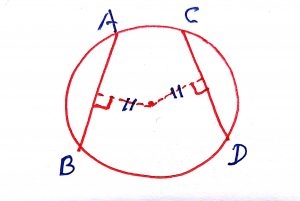
If two chords AB and CD of a circle intersect at P (Internally or externally) then,
Geometry Concept: 99 SECANT THEOREM
If through a point outside a circle a tangent and chord be drawn, then the square of the length of the tangent is equal to the rectangle contained by the segments of the chord.
COMMON TANGENTS TO TWO CIRCLE
In this section, you will learn Geometry Concept Tips and Tricks of Tangents Related to Circles.
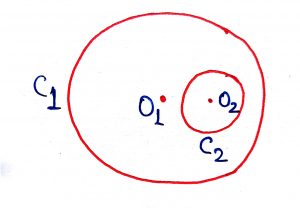
Geometry Concept: 100 NUMBER OF COMMON TANGENTS
Let two circles C1 and C2 with centers O1 and O2 with radii R and r respectively with R > r and the distance between their centers is d, then the number of the common tangents that can be drawn to them varies from zero to four in the same plane of the circle depending upon the relative positions of the circles.
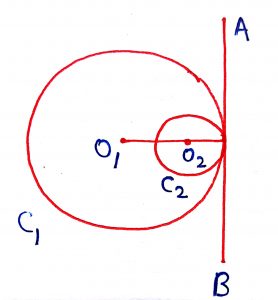
Case 1: The circle C2 lies wholly within C1 and the two circles do not touch other means
Number of Common Tangent = 0
Case 2: The circle C2 lies wholly within C1 and touches it internally at a point P means
Number of Common Tangent = 1
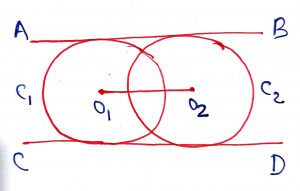
Case 3: The circle C1 and C2 intersect each other at two points means
Number of Common Tangent = 2
Case 3: The circle C1 and C2 touch each other externally means
Number of Common Tangent = 3
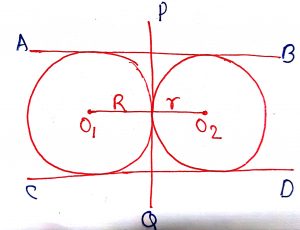
Case 4: The circle C2 lies outside from the circle C1 and the two circles do not intersect each other means
Number of Common Tangent = 4
Geometry Concept: 101 DIRECT AND TRANSVERSE TANGENTS
The direct common tangents to two circle intersects each other at a point on the line joining the centers. This point divides the line joining the centers externally in the ratio of their radii.
The transverse common tangents to two circles also intersect each other at a point on the line joining the centers. This point divides the line joining the centers internally in the ratio of their radii.
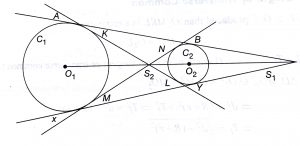
In the figure, The circle C1 and C2 do not intersect. In this case, there are four common tangents, two direct common tangents AB and XY and two transverse common tangents KL and MN.
The two direct common tangents AB and XY intersect at S1. The point S1 divides O1O2 externally in the ratio R:r. It means .
Similarly, the two transverse tangents KL and XY intersect at S2. The point S2 divides O1O2 internally in the ratio R:r. It means .
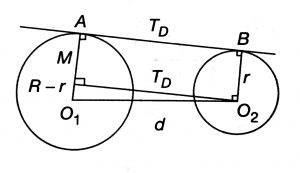
Geometry Concept: 102 LENGTH OF DIRECT COMMON TANGENTS
In the given figure, O1A = R and O2B = r, O1O2 = d and AB = TD = Length of Direct Common Tangent.
Then,
If two circles touche each other externally then d = R + r. Thus,
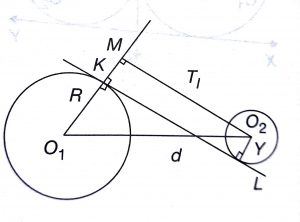
Geometry Concept: 103 LENGTH OF TRANSVERSE COMMON TANGENTS
In the given figure, O1K = R and O2L = r, O1O2 = d and KL = TI = Length of Transverse Common Tangent.
Then,
If two circles touche each other externally then d = R + r. Thus,
CYCLIC AND TANGENTIAL
In this section, you will learn Geometry Concept Tips and Tricks of Cyclic Quadrilateral and Tangential Quadrilaterals.
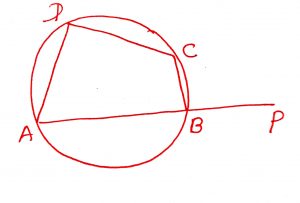
Geometry Concept: 104 CYCLIC QUADRILATERAL
A quadrilateral which has a circle passing through all its four vertices is called a CYCLIC QUADRILATERAL. The sum of each pair of opposite angles is 180 degree. The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle. In the figure, ABCD is a cyclic quadrilateral. Then,
and
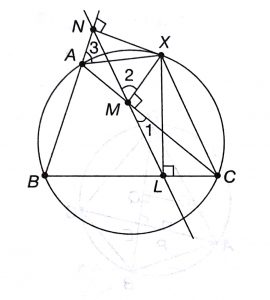
Geometry Concept: 105 SIMSON WALLACE LINE
The feet L, M, N of the perpendiculars on the sides BC, CA, AB of any triangle ABC from any point X on its circumcircle of the triangle ABC are collinear. The line LMC is called the SIMSON WALLACE LINE.
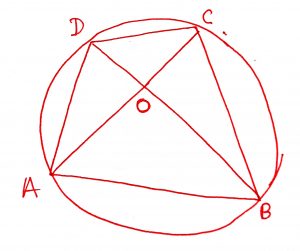
Geometry Concept: 106 PTOLEMY THEOREM FOR CYCLIC QUADRILATERAL
In a cyclic quadrilateral, the product of the diagonals is equal to the sum of the product of the pair of opposite sides. In the figure, ABCD is a cyclic quadrilateral. Then, AB CD + AD
BC = AC
BD.
Geometry Concept: 107 PTOLEMY THEOREM FOR ANY QUADRILATERAL
For any quadrilateral, the product of the diagonals is less than or equal to the sum of the product of the pairs of opposite sides. Equality holds for cyclic quadrilateral.
In the figure, ABCD is a any quadrilateral. Then,
For cyclic quadrilateral, A + C = 180 degree cos(A+ C) = cos(180) = –1
AC
BD = AB
CD + AD
BC
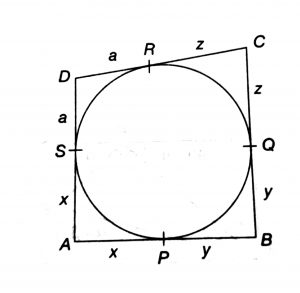
Geometry Concept: 108 PITOT THEOREM
If a circle is inscribed in a quadrilateral ABCD, then the sum of opposite sides are equal. it means AB + CD = AD + BC.
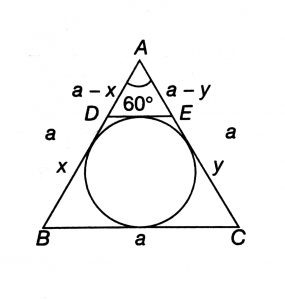
Geometry Concept: 109 IMPORTANT RESULT
Triangle ABC is equilateral triangle. D is on AB and E is on AC such that DE is tangent to the incircle Then,
AREAS
In this section, you will learn Geometry Concept Tips and Tricks of Area of Geometrical Figures.
Geometry Concept: 110 AREA OF TRIANGLE
There are following formula to find the area of the triangle.
Area of Triangle =
Area of Triangle = Product of Two Sides
Sin (Included Angle between the Two sides)
Area of Triangle = , where
Geometry Concept: 111 AREA OF QUADRILATERAL
There are following formula to find the area of the quadrilateral.
Area of Quadrilateral = Product of Two Diagonals
Sin (Included Angle between the Two Diagonals)
Area of Quadrilateral = , where
For cyclic quadrilateral, the sum of opposite angles = 180 degree. Then,
Thus, Area of Cyclic Quadrilateral = .
Geometry Concept: 112 AREA OF REGULAR POLYGON
There are following formula to find the area of the regular polygon.
In terms of its side, Let the side of the regular polygon is s and the number of its sides = n, then
Area of Regular Polygon =
CENTERS OF TRIANGLE
In this section, you will learn Geometry Concept Tips and Tricks of Centers of Triangle.
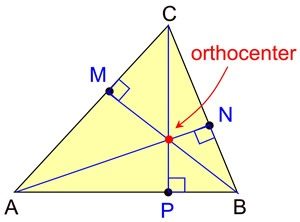
Geometry Concept: 113 ORTHOCENTER (O)
The point of intersection of altitudes from the vertices to the opposite sides of a triangle is known as the orthocenter of the triangle.
Orthocenter of an obtuse angled triangle lies outside the triangle and behind the obtuse angle.
Orthocenter of an acute angled triangle lies inside the triangle.
Orthocenter of a right angled triangle is at the right angle vertex.
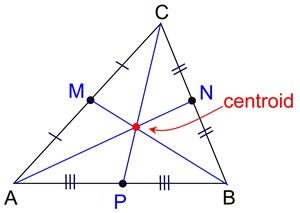
Geometry Concept: 114 CENTROID
In a triangle ABC, the mid-points of the sides BC CA and AB are D E and F respectively. The lines AD BE and CF are called medians of the triangle ABC, the point of concurrency of the three medians is called centroid.
The centroid divides the medians in the ratio of 2:1 from the vertex to the side. The centroid is denoted by G. Then,
(i) (ii)
,
,
(iii)
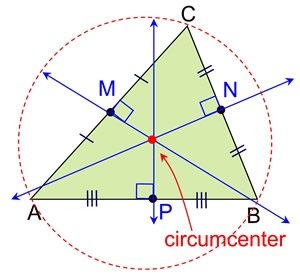
Geometry Concept: 115 CIRCUMCENTER
The point of intersection of perpendicular bisectors of the sides of a triangle is known as the circumcenter of the triangle.
It is the center of the circle which passes through the vertices of the triangle and the circle is known as circumcircle. The radius of the circumcircle is known as circum radius R.
Circumcenter is equidistant from the vertices of the triangle.
Circumcenter of an obtuse angled triangle lies outside the triangle.
Circumcenter of an acute angled triangle lies inside the triangle.
Circumcenter of a right angled triangle is at the mid-point of the hypotenuse.
Circumradius R = , where a, b and c are the sides of the triangle and
is the area of the triangle.
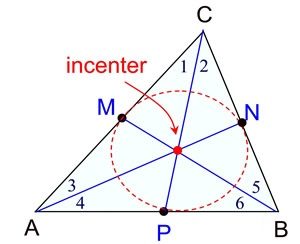
Geometry Concept: 116 INCENTER
The point of intersection of angle bisectors of a triangle is known as the incenter of the triangle.
It is the center of the circle touches the sides of the triangle and the circle is known as incircle. The radius of the incircle is known as inradius r.
Incenter is equidistant from the sides of the triangle.
Incenter of always lies inside in any triangle.
Inradius r = , where
is the area of the triangle and s is the semiperimeter.
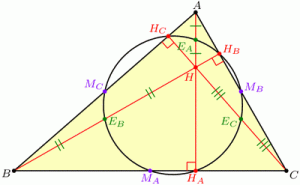
Geometry Concept: 117 NINE POINT CENTER (N)
A circle passing through nine fixed points which are
(i) Three mid-points of sides of a triangle
(ii) Three feet of its altitudes
(iii) Three mid-points the line segment joining the orthocenter and vertex.
Thus, the circle passing through these nine fixed points is known as Nine Point Circle and its center is known as nine Point Center.
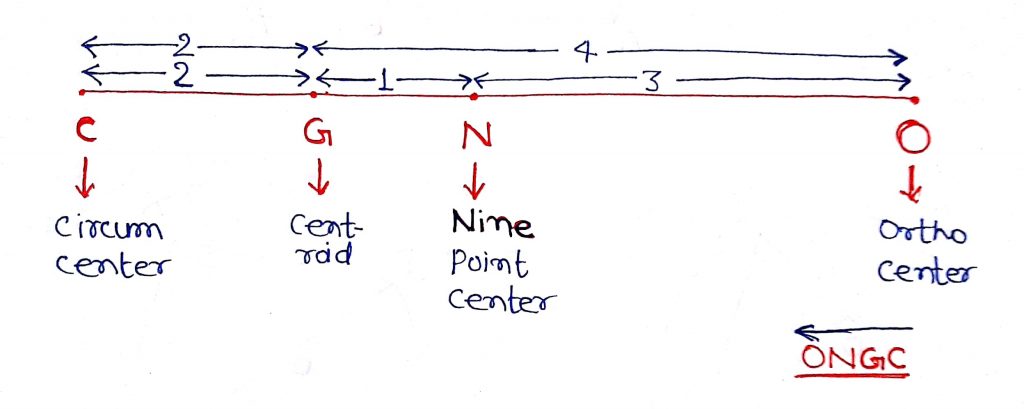
Geometry Concept: 118 ONGC
In any triangle, the orthocenter (O), the nine point center (N), the centeroid (G) and the circumcenter (C) are collinear.
The nine point center (N) is the mid-point of the orthocenter (O) and the circumcenter (C).
The radius of the nine point circle is the half of the circumradius of the triangle.
The centeroid (G) divides the line segment joining the orthocenter (O) and circumcenter (C) internally in the ratio of 2 : 1.
COSINE FORMULA
In this section, you will learn Geometry Concept Tips and Tricks of Cosine Formulas.
Geometry Concept: 119 COSINE FORMULA FOR ANY TRIANGLE
If ABC is a triangle whose sides are BC = a, CA = b and AB = c, then
(i)
(ii)
(iii)
Geometricks EBook
Geometry Concept 120: In Geometrick EBook PDF
Hi Students, I am AMAN RAJ, founder of www.AmansMathsBlogs.com. I have released a PDF of geometry and mensuration tips and tricks and named it as GEOMETRICKS EBook. It contains approx all the tips and tricks of geometry and mensuration topics. There are total 356 geometry and mensuration tips and tricks in this ebook. (including this 119 Geometry Concepts of this post). For more details about this ebook, Click Here.







tnx bro..it is very helpful for ssc exam