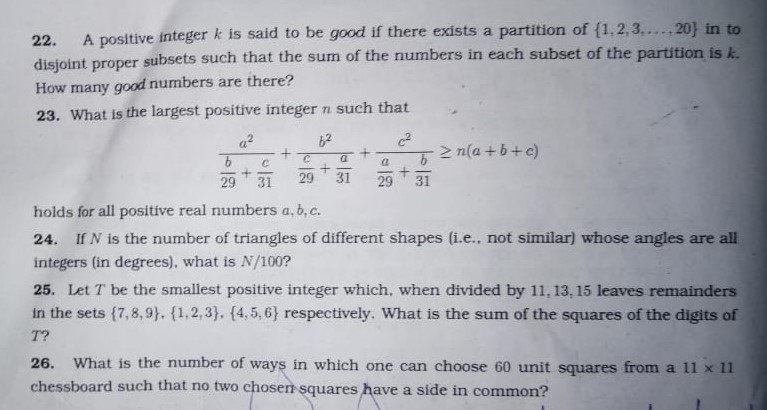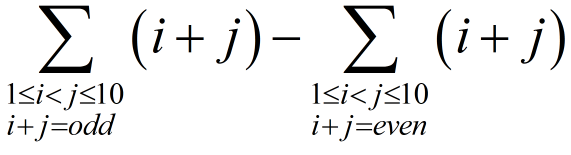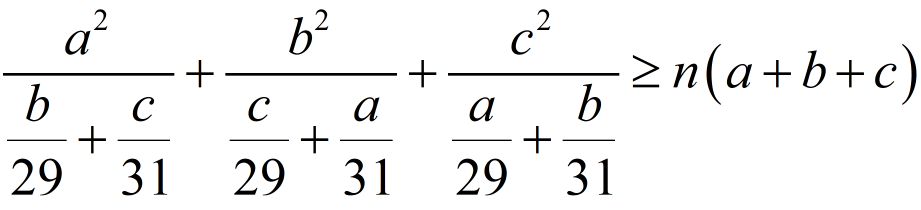Pre RMO 2018 Question Paper With Solutions

In this post, you will get Pre RMO 2018 Question Paper With Solution.

Read: Pre RMO and RMO Important Study Materials: Books | PDFs | Blogs | YouTube Channels | Solved Papers

Pre RMO 2018 Question Paper With Solution of Q No 1

A book is published in three volumes, the pages being membered from 1 onwards. The page numbers are continued from the first volume to the second volume to the third. The number of pages in the second volume is 50 more than that in the first volume, and the number pages in the third volume is one and a half times that in the second. The sum of the page numbers on the first pages of the pages of the three volumes is 1709. If n is the last page number, what is the largest prime factor of n?

Solution:

Pre RMO 2018 Question Paper With Solution of Q No 2

In a quadrilateral ABCD, it is given that AB = AD = 13, BC = CD = 20, DB = 24. If the r is the radius of the circle inscribable in the quadrilateral, then what is the integer closest to r?

Solution:

Pre RMO 2018 Question No 3

Consider all 6-digit numbers of the form abccba where b is odd. Determine the number of all such 6-digit numbers that are divisible by 7.

Solution:

Pre RMO 2018 Question No 4

The equation 166 x 56 = 8590 is valid in some base b >= 10 (that is, 1, 6, 5, 8, 9, 0 are digits in base b in the above equation). Find the sum of all possible values of b >= 10 satisfying the equation.

Solution:

Pre RMO 2018 Question No 5

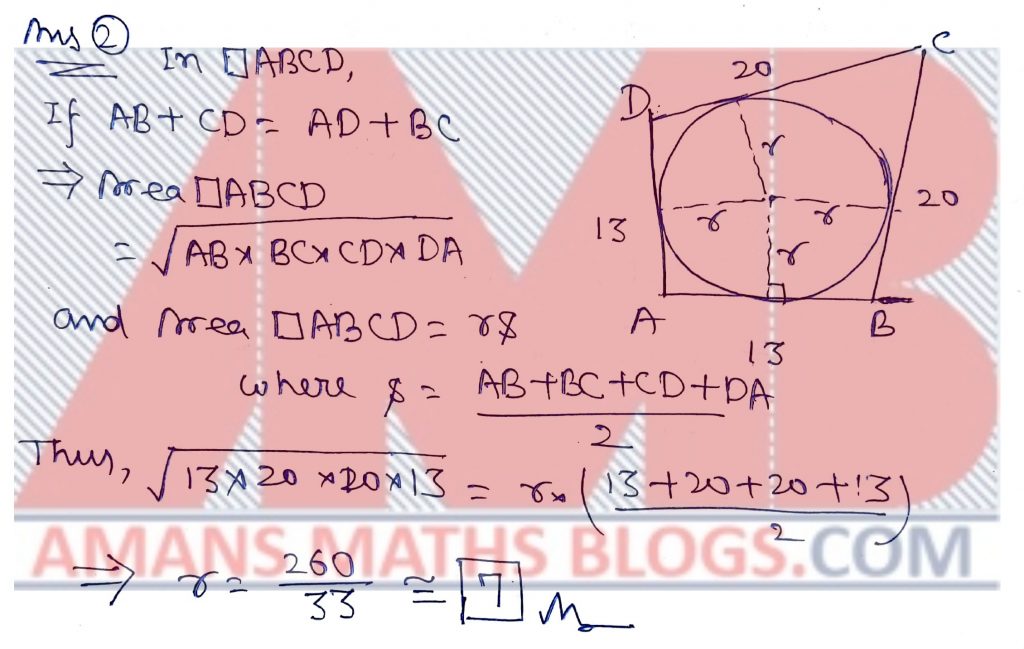
Let ABCD be a trapezium in which AB || CD and AD $\perp$ AB. Suppose ABCD has an incircle which touches AB at Q and CD at p. Given that PC = 36 and QB = 49, find PQ.

Solution:

Pre RMO 2018 Question No 6

Integers a, b, c satisfy a + b – c = 1 and a² + b² – c² = –1. What is the sum of all possible values of a² + b² + c²?

Solution:

Pre RMO 2018 Question No 7

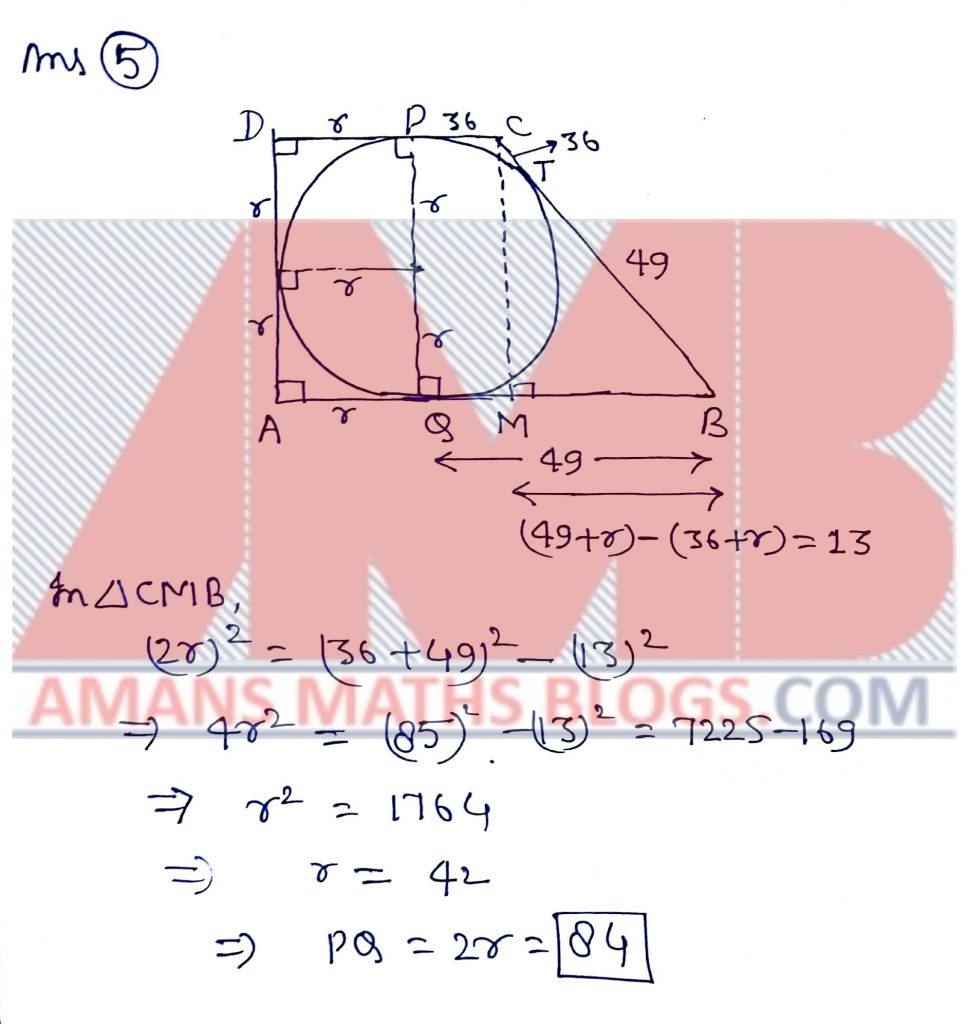
A point P in the interior of regular hexagon is at distance 8,8,16 units from three consecutive verticals of the hexagon respectively. If r is radius of the circumscribed circle of the hexagon, what is the integer closest to r?

Solution:

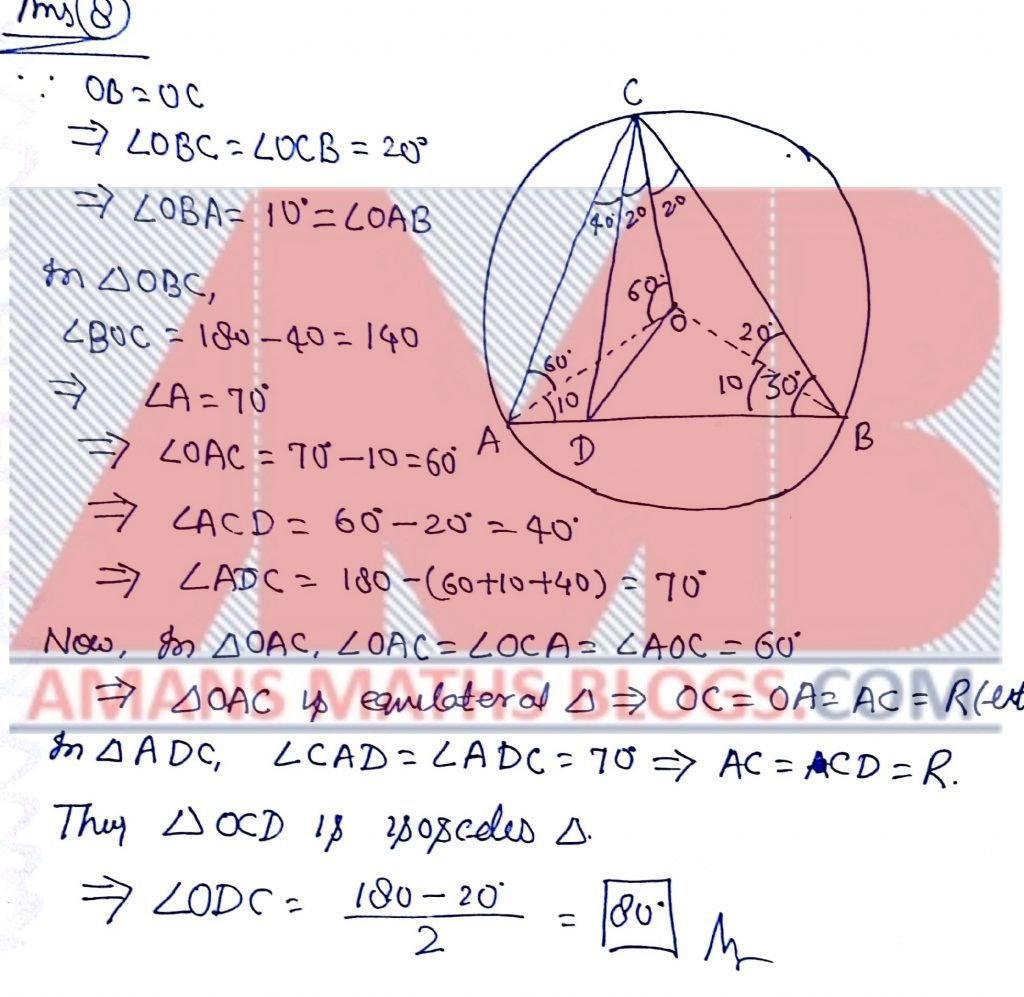
Pre RMO 2018 Question No 8

Let AB be a chord of a circle with center O. Let C be a point on the circle such that ABC = 30 degree and O lies inside the triangle ABC. Let D be a point on AB such that angle DCO = angle OCB = 20 degree, find the measure of angle CDO in degrees.

Solution:

Pre RMO 2018 Question No 9

In a triangle ABC, the median and a + b is root of x² + ax + b = 0. What is the maximum possible value of b²?

Solution:

Pre RMO 2018 Question No 10

In a triangle ABC, the median from B to CA is perpendicular to the median from C to AB. If the median from A to BC is 30, determine (BC² + CA² + AB²)/100.

Solution:

Pre RMO 2018 Question No 11

There are several tea cups in the kitchen, some with handles and the others without handles. The numbers of ways of selecting two cups without a handle and three with a handle in exactly 1200. What is the maximum possible number of cups in the kitchen?

Solution:

Pre RMO 2018 Question No 12

Determine the number of 8-tuples ( $\epsilon_{1},\epsilon_{2},...,\epsilon_{8},$ ) such that {1,–1} and $\epsilon_{1}+2\epsilon_{2}+3\epsilon_{3}+...+8\epsilon_{8}$ is a multiple of 3.

Solution:

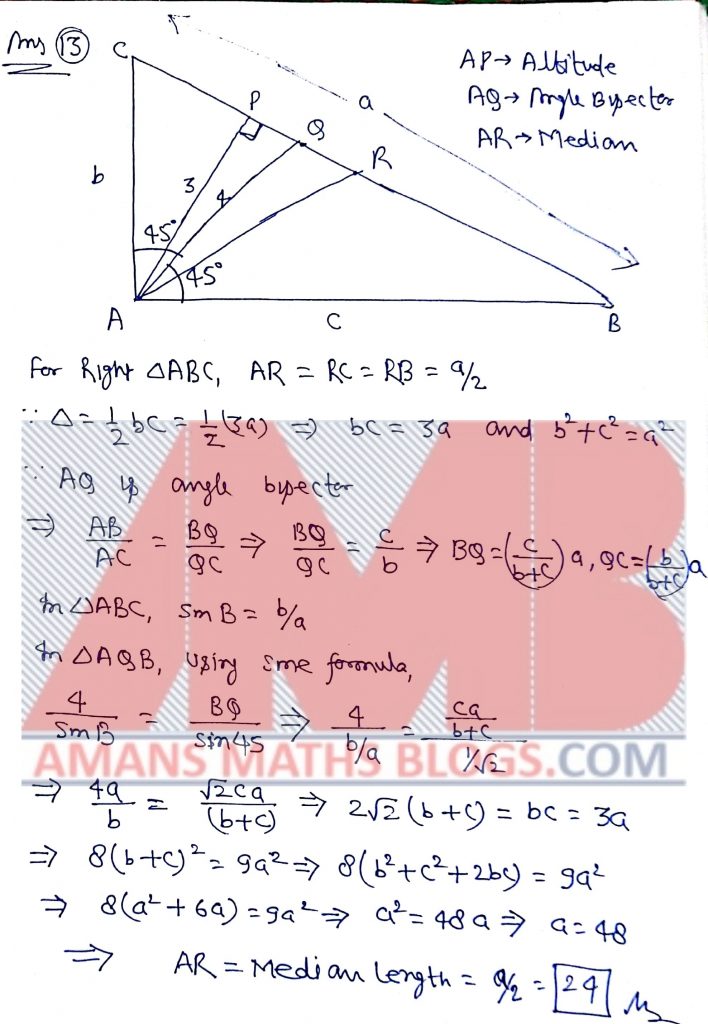
Pre RMO 2018 Question No 13

In a triangle ABC, right-angled at A, the altitude through A and the internal bisector of angle A, have lengths 3 and 4, respectively. Find the length of the median through A.

Solution:

Pre RMO 2018 Question No 14

If x = cos1cos2cos3…cos89 and y = cos2cos6cos10…cos86, then what is the integer nearest to (2/7)log₂(y/x)?

Solution:

Pre RMO 2018 Question No 15

Let a and b be natural numbers such that 2a – b, a – 2b and a + b are all distinct square. What is the smallest possible value of b?

Solution:

Pre RMO 2018 Question No 16

What is the value of

Solution:

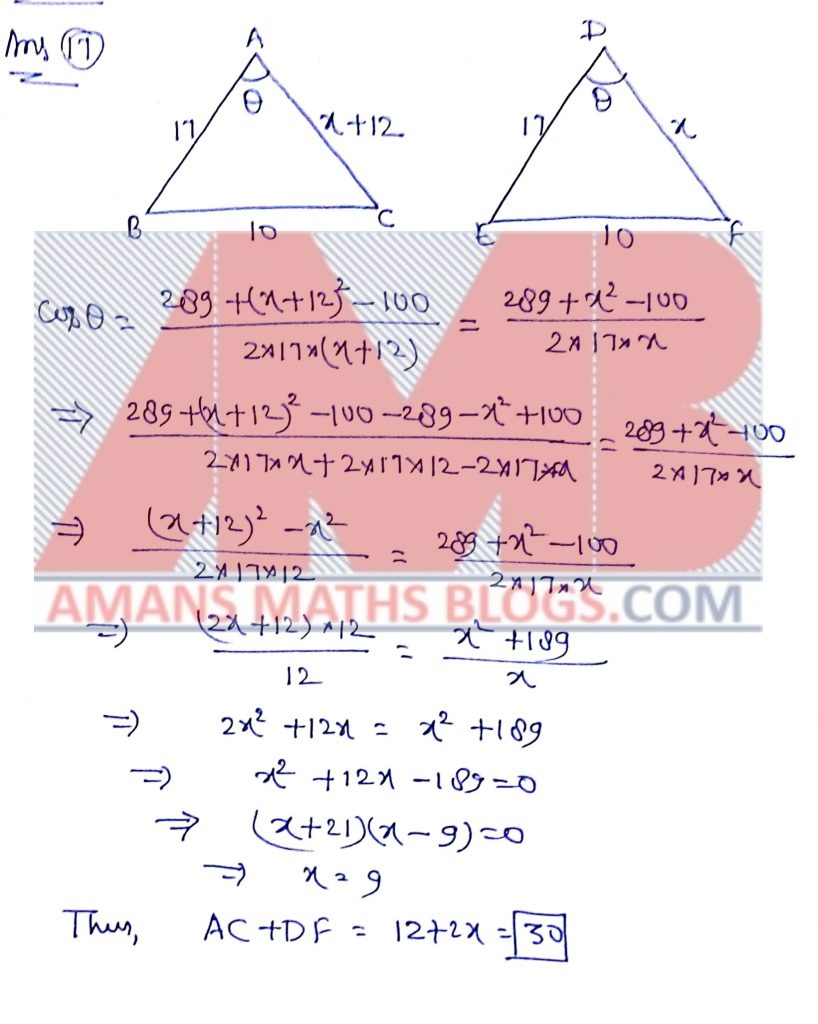
Pre RMO 2018 Question No 17

Triangles ABC and DEF are such that angle A = angle D, AB = DE = 17, BC = EF = 10 and AC – DF = 12. What is AC + DF?

Solution:

Pre RMO 2018 Question No 18

If a, b, c >= 4 are integers, not all equal, and 4abc = (a + 3)(b + 3)(c + 3), then what is the value of a + b + c?

Solution:

Pre RMO 2018 Question No 19

Let N = 6 + 66 + 666 + ….+ 666…66, where there are hundred 6’s in the last term in the sum. How many times does the digit 7 occur in the number N?

Solution:

Pre RMO 2018 Question No 20

Determine the sum of all possible integers n, the product of whose digits equals n² – 15n – 27.

Solution:

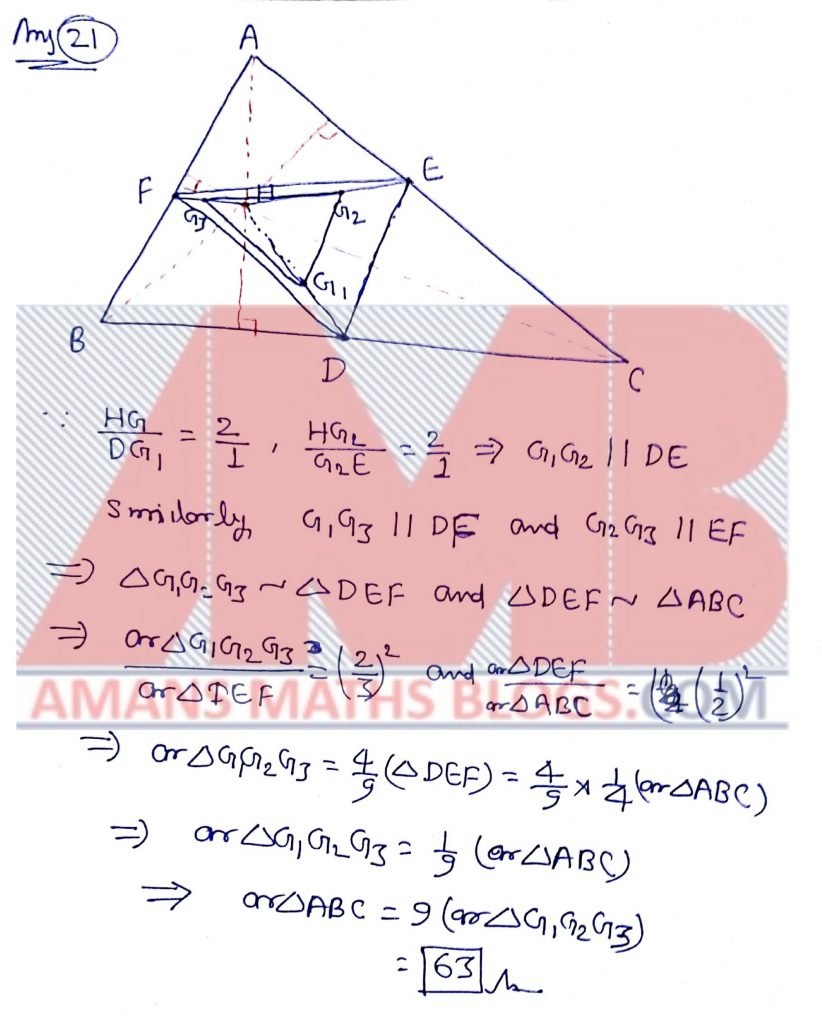
Pre RMO 2018 Question No 21

Let ABC be an acute-angled triangle and let H be its orthocenter. Let G₁, G₂ and G₃ be the centroids of the triangles HBC, HCA and HAB, respectively. If the area of triangle G₁G₂G₃ is 7 units, what is the area of triangle ABC?

Solution:

Pre RMO 2018 Question No 22

A positive integer k is said to be good if there exists a partition of {1, 2, 3,….20} in to disjoint proper subsets such that the sum of the numbers in each subset of the partition is k. How many good numbers are there?

Solution:

Pre RMO 2018 Question No 23

What is the largest positive integer such that

holds for all positive real numbers a, b, c?

Solution:

Pre RMO 2018 Question No 24

If N is the number of triangles of different shapes (i.e., not similar) whose angles are all integers (in degrees), what is N/100?

Solution:

Pre RMO 2018 Question No 25

Let T be the smallest positive integer which, when divided by 11, 13, 15 leaves remainders in the sets {7, 8, 9}, {1, 2, 3}, {4, 5, 6} respectively. What is the sum of the square of the digit of T?

Solution:

Pre RMO 2018 Question No 26

What is the number of ways in which one can choose 60 unit square from a 11 x 11 chessboard such that no two chosen squares have a side in common?

Solution:

Pre RMO 2018 Question No 27

What is the number of ways in which one can colour the squares of a 4 x 4 chessboard with colours red and blue such that each row as well as each columns has exactly two red squares and two blue squares?

Solution:

Pre RMO 2018 Question No 28

Let N be the number of ways of distributing 8 chocolates of different brands among 3 children such that each child gets at least one chocolate, and two children get the same number of chocolates. Find the sum of the digits of N.

Solution:

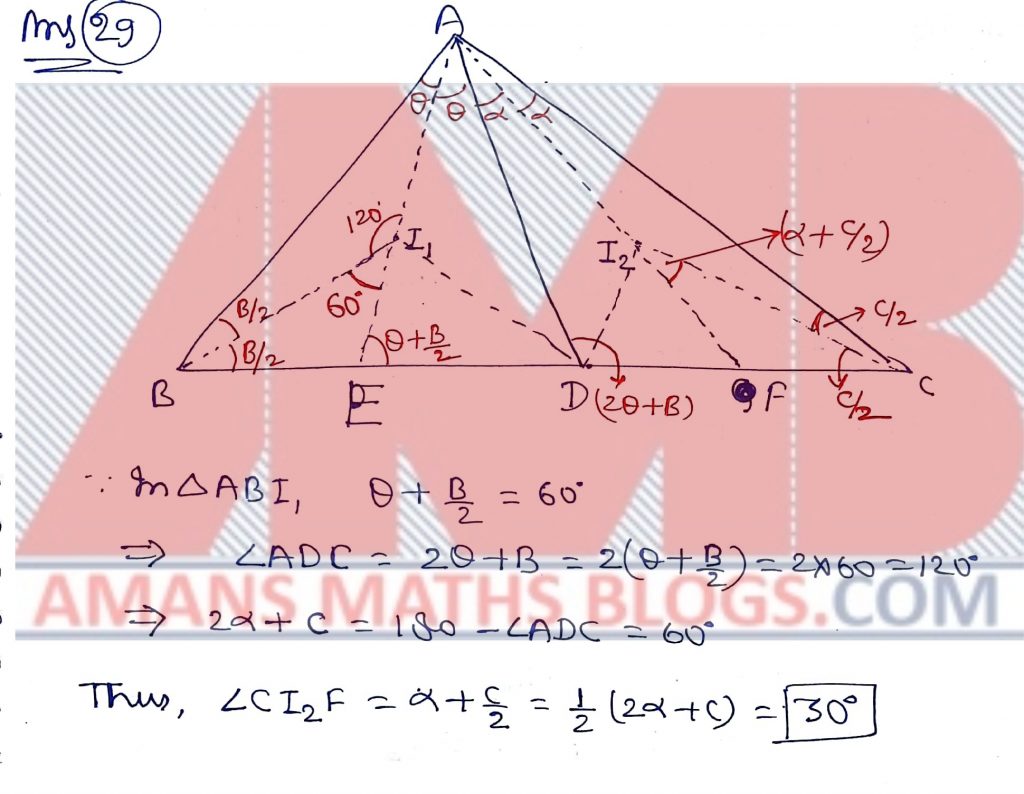
Pre RMO 2018 Question No 29

Let D be an interior point of the side BC of a triangle ABC. Let I₁ and I₂ be the incetres of triangle ABD and ACD respectively. Let AI₁ and AI₂ meet BC in E and F respectively. If BI₁E = 60 Degree, what is the measure of CI₂F in degrees?

Solution:

Pre RMO 2018 Question No 30

Let P(x) = a₀ + a₁x + a₂x₂ + ….+ a_nx_n be a polynomial in which is a_i is a non-negative integer for each i $\in$ {0, 1, 2, 3,….,n}. If P(1) = 4 and P(5) = 136, what is the value of P(3)?