Distance Between Two Points or Distance Formula

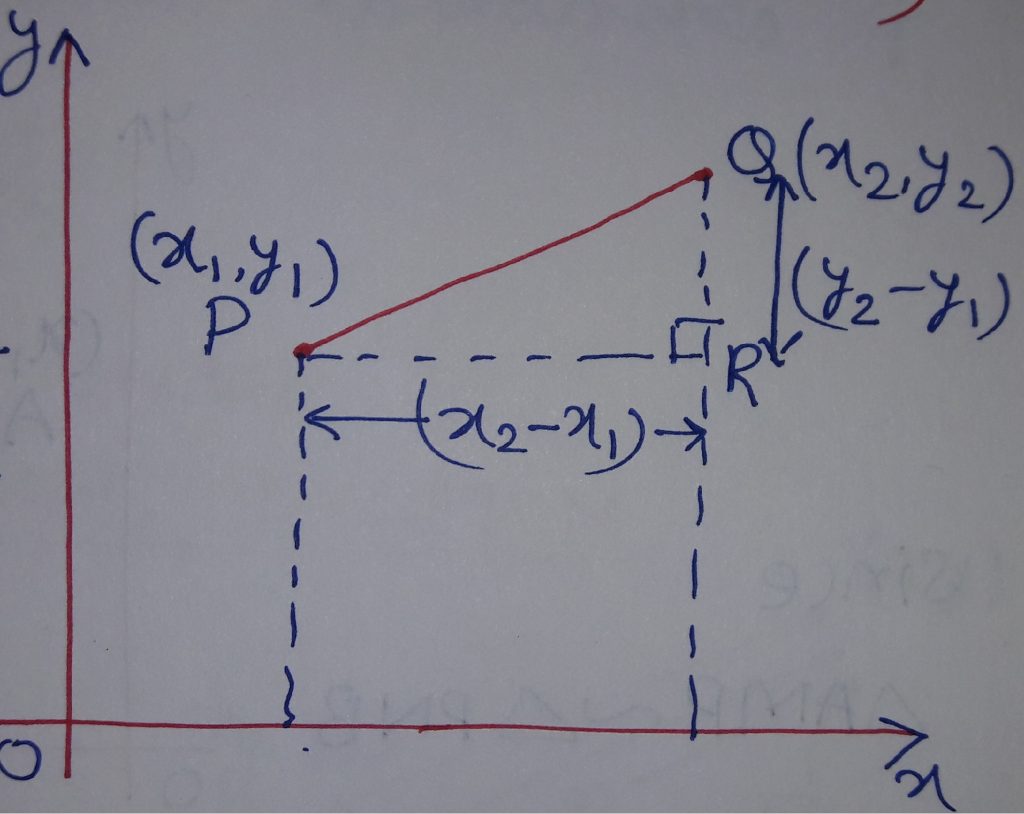
In this post, we will learn the distance formula. We need to find the distance between two points on Rectangular Coordinate Plane. For this, take two points in XY plane as P and Q whose coordinates are P(x₁, y₁) and Q(x₂, y₂). We join P and Q and make a right triangle PQR as shown in the figure below.

Thus, we need to find PQ.

From the figure, we have PR = (x₂-x₁) and QR  = (y₂-y₁). 

In right triangle PQR, we use Pythagoras Theorem as

PQ² = PR² + QR² = (x₂-x₁)² + (y₂-y₁)²  PQ = 

Thus, the distance between two points P(x₁, y₁) and Q(x₂, y₂) is

Some Important Points Related to Distance Formula

1. If O is the origin and P(x, y) is any point, then from distance formula OP = 

2. For three points to be collinear, the sum of the distance between two pairs of points is equal to the third pair of the points. 

3. Given the two points (x₁, y₁) and (x₂, y₂), they only indicate that there is a “first” point and a “second” point; that is, that you have two points. Whichever one you call “first” or “second” is up to you. The distance will be the same, regardless.

4. The most common mistake made when using the Formula is to accidentally mismatch the x-values and y-values. Be careful you don’t subtract an x from a y, or vice versa; make sure you’ve paired the numbers properly.

5. If three coordinates of three vertices are given in an order, then to prove that the given vertices are of an isosceles triangle, we have to prove that at least two sides are equal by using the distance formula.

6. If three coordinates of three vertices are given in an order, then to prove that the given vertices are of an equilateral triangle, we have to prove that all three sides are equal by using the distance formula.

7. If three coordinates of three vertices are given in an order, then to prove that the given vertices are of a right triangle, we have to prove that the sum of squares of any two sides is equal to the square of third side by using the distance formula.

8. If four coordinates of four vertices are given in an order, then to prove that the given vertices are of a square, we have to prove that all four sides are equal by using the distance formula.

9. If four coordinates of four vertices are given in an order, then to prove that the given vertices are of a rhombus, we need to prove that four sides are equal by using the distance formula. (In this case, there is no need to prove that the diagonals are unequal as square is also a kind of rhombus).

10. If four coordinates of four vertices are given in an order, then to prove that the given vertices are of a rectangle, we have to prove that the opposite sides and two diagonals are also equal by using the distance formula. 

11. If four coordinates of four vertices are given in an order, then to prove that the given vertices are of a parallelogram, we need to prove that the opposite sides are equal by using the distance formula. (In this case, there is no need to prove that two diagonals are unequal as the rectangle is also a kind of parallelogram)

See this video about How To Find the Distance Between Two Points:

Practice Some Questions of Distance Formula

Question No 1 : Find the distance between the points (8, -2) and (3, -8).

Ans : sqrt(41)

Question No 2 : Prove that the points (1, -1), (-1/2, 1/2) and (1, 2) are the vertices of an isosceles triangle. 

Question No 3 : Using distance formula, show that the points (-3, 2), (1, -2) and (9, -10) are collinear.

Question No 4 : Find a point on the x-axis which is equidistant from the points (5, 4) and (-2, 3)

Ans : (2, 0)

Question No 5 : The vertices of a triangle are (-2, 0), (2, 3) and (1, -3) is the triangle equilateral, isosceles, or scalene triangle?

Ans : Scalene Triangle

Question No 6 : The length of a line-segment is 10. If one end is at (2, -3) and the abscissa of the second end is 10, show that its ordinate is either 3 or -9.

Question No 7 : Show that the points (-2, 5), (3, -4) and (7, 10) are the vertices of a right angled triangle.

Question No 8 : If the distance of P(x, y) from A(5, 1) and B(-1, 5) are equal, then prove that 3x = 2y.

Question No 9 : If the vertices of a triangle are (2, 1), (5, 2) and (3, 4), then find the coordinate of its circumcentre.

Ans : (13/4, 9/4)

Question No 10 : Find the point P(x, y) if its distance from (-3, 0) and (3, 0) is 4 units individually.

Ans : (0, -sqrt(7))

Question No 11 : Find the point on y-axis which is equidistant from A(-5, -2) and B(3, 2)

Ans : (0, -2)

Question No 12 : If the points (0, 2) is equidistant from the points (3, k) and (k, 5), then find the value of k

Ans : k = 1

Question No 13 : What point on x-axis is equidistant from (7, 6) and (-3, 4)?

Ans : (3, 0)

Question No 14 : If the point (x, y) be equilateral from the points (a+b, b-a) and (a-b, a+b), then prove that bx=ay.

Question No 15 : Show that (1, -1) is the center of the circle circumscribing the triangle whose angular points are (4, 3), (-2, 3) and (6, -1).

Question No 16 : Show that the points A(7, 5), B(2, 3) and C(6, -7) are the vertices of a right triangle. Also find the area.

Ans : 29 sq. units

Question No 17 : Show that A(a, a), B(-a, -a) and C(-a√3, a√3) form an equilateral triangle.

Question No 18 : Show that A(5, 6), B(1, 5), C(2, 1) and D(6, 2) are the vertices of a square.

Question No 19 : Show that A(2, -2), B(14, 10), C(11, 13) and D(-1, 1) are the vertices of a rectangle.

Question No 20 : Show that A(-2, 3), B(8, 3) and C(6, 7) are the vertices of a right angled triangle.

coordinate geometrydistance formula definitiondistance formula examplesdistance formula problemsdistance formula worksheetfind the distance between two points calculatorhow to find the midpoint between two pointsmaths blog